The k-th element in the array [heap row + actual time complexity of heap building]

Preface

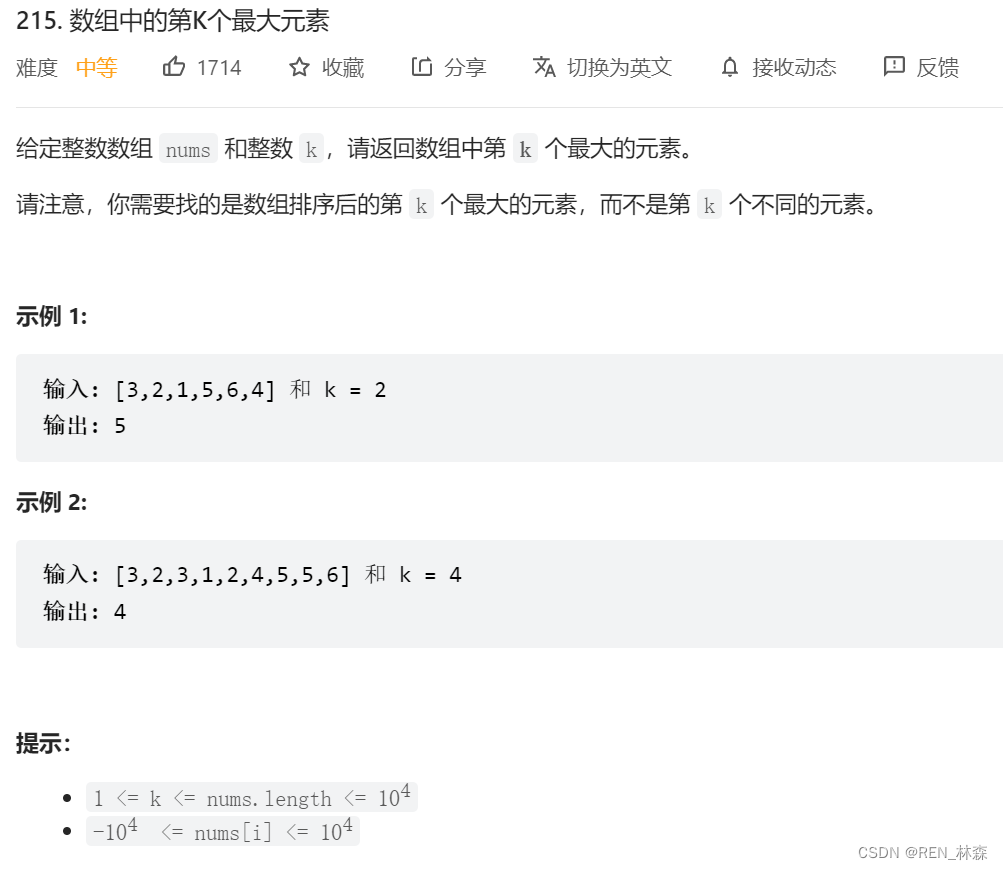
The heap can be arranged without complete sorting , Take second place K Big element , But the same is true of selective sorting .

So who will run faster ？ When building a reactor , Need to adjust n/2 Time , The maximum depth of each time is log₂(n), The first visual impression is to build a pile T(n) = O(nlgon), It's not .

Heap discharge k The time of the big element = Build time + take k The time of the first element = (O(n) - O(log₂n) - 1) + O(klog₂n) = O(n);
Select sort to get k The time of the big element = O(kn) = O(n).

because (O(n) - O(log₂n) - 1) + O(klog₂n) <O(kn), So stack faster .

The proof is in the comments before the second part of the code .

One 、 The... In the array K Big element

Two 、 Proof of reactor building complexity

prove ： Take the full binary tree with the most nodes as an example , Tree height is h,

Set the current layer as k, Then this layer has 2^(k - 1)^ Nodes , Each node needs to be adjusted h - k The depth of the .

therefore ,T(n) = 2⁰ * (h - 1) + 2¹ * (h - 2) +…+2^(h - 2) * 1, Obviously, it is a typical difference ratio sequence , Just offset and subtract .

2T(n) = 2¹ * (h - 1) + 2² * (h - 2) +…+2^(h - 2)^ * 2 + 2^(h - 1) * 1,

The difference between the two formulas is T(n) = 2^h - h - 1, notes ：h = log2(n), therefore T(n) = O(n) - O(log2(n)) - 1 = O(logn)

notes ： Computational complexity , The premise is that n Large enough , If n Very small , There is no complexity , direct O(1)

3、 ... and 、 Quick line up / Priority queue / Stack row

package everyday.medium;

import java.util.PriorityQueue;

//  No k The biggest element .
public class FindKthLargest {
    /* target： Take the second in the array K Big element , Put the array in order , take nums[k - 1] that will do , But the time complexity O(nlogn), Not an option .  Selection sort , Select the first K individual , Time complexity O(kn), namely O(n), feasible .  Stack row , It takes time to build a pile O(nlogn), Choose the first k Big , flowers O(klogn), Time complexity O( ), Is not workable .  Why does it take to build a pile O(nlogn)？ Our intuitive feeling , To adjust n/2 Time ( Adjust from the penultimate line ), Adjust downward each time O(logn)( Naturally took the biggest one ).  So building a pile takes O(nlogn). But this is an illusion . The actual time complexity is Tn = 2^log2(n)^ - log2(n) - 1 =O(n) - O(logn) = O(n)( When n When a large )  prove ： Take the full binary tree with the most nodes as an example , Tree height is h,  Set the current layer as k, Then this layer has 2^(k - 1)^ Nodes , Each node needs to be adjusted h - k The depth of the .  therefore ,T(n) = 2^0^ * (h - 1) + 2^1^ * (h - 2) +...+2^(h - 2) * 1, Obviously, it is a typical difference ratio sequence , Just offset and subtract . 2T(n) = 2^1^ * (h - 1) + 2^2^ * (h - 2) +...+2^(h - 2)^ * 2 + 2^(h - 1) * 1,  The difference between the two formulas is T(n) = 2^h^ - h - 1, notes ：h = log2(n), therefore T(n) = O(n) - O(log2(n)) - 1 = O(logn)  notes ： Computational complexity , The premise is that n Large enough , If n Very small , There is no complexity , direct O(1) */
    //  Selection sort  --  Although it is O(n), But time is Tn = kn, Compared with stacking ,Tn = n - log(n+1) + klogn, Still a lot slower .
    public int findKthLargest(int[] nums, int k) {
        for (int i = 0; i < k; i++) {
            //  choice 
            int max = nums[i], idx = i;
            for (int j = i + 1; j < nums.length; j++) {
                if (max < nums[j]) {
                    max = nums[j];
                    idx = j;
                }
            }
            // swap
            int t = nums[idx];
            nums[idx] = nums[i];
            nums[i] = t;
        }
        //  Value 
        return nums[k - 1];
    }

    //  Stack row , skilled API, Priority queue , The whole big top pile .
    public int findKthLargest2(int[] nums, int k) {
        //  Big pile top 
        PriorityQueue<Integer> que = new PriorityQueue<>((o1, o2) -> o2 - o1);
        //  Add elements 
        for (int num : nums) que.offer(num);
        //  The first 1 - (k-1) Large elements are taken out 
        for (int i = 0; i < k - 1; i++) que.poll();
        //  Take the first place K Big 
        return que.poll();
    }

    //  Stack row ,API There are too many encumbrances , Direct stacking .
    public int findKthLargest3(int[] nums, int k) {
        //  Building the heap , Start from the node with children on the penultimate layer .
        for (int i = nums.length - 1 >>> 1; i >= 0; i--) adjustHeap(nums, i, nums.length);
        //  Front row K A big element comes out .
        int i = 0;
        do {
            // swap
            int t = nums[0];
            nums[0] = nums[nums.length - 1 - i];
            nums[nums.length - 1 - i] = t;
            //  Adjust the heap , Make the top of the heap the largest element .
            if (++i >= k) break;
            adjustHeap(nums, 0, nums.length - i);
        } while (true);
        //  Take the first place k The biggest element 
        return nums[nums.length - k];
    }

    //  Stack core ： Adjust the heap 
    private void adjustHeap(int[] nums, int k, int end) {
        int ori = nums[k]; //  Remember the original elements to adjust .
        //  Keep adjusting downward 
        for (int i = (k << 1) + 1; i < end; i = (i << 1) + 1) {
            //  Whether the left child or the right child is older .
            if (i + 1 < end && nums[i + 1] > nums[i]) ++i;
            //  See if it is necessary to exchange with the child .
            if (ori >= nums[i]) break;
            //  Downward adjustments 
            nums[k] = nums[i];
            //  Get the new position of the original element .
            k = i;
        }
        //  Put the original element in the space it was last swapped to .
        nums[k] = ori;
    }
}

summary

1） The time complexity of building a heap is O(n), No O(nlogn).
2） Priority queue / Stack row / Selection sort .

reference

LeetCode The... In the array K Big element