当前位置:网站首页>第三章-函数的增长-3.1-渐近记号
第三章-函数的增长-3.1-渐近记号
2022-08-02 14:21:00 【学编程的Jerry】
引入:渐近记号的引入是用来刻画算法的运行时间。
一、Θ记号
1、概念
书上原话:
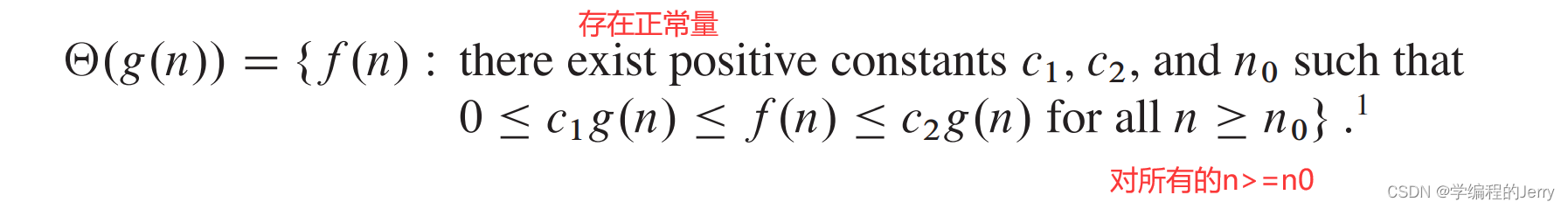
如何理解?
存在正 常量c1、c2,使当n足够大的时候,f(n)可以被夹在c1*g(n)和c2*g(n)之间,则称f(n) ∈ θ(g(n)),但是我们通常会表示为f(n) = θ(g(n)),如图,
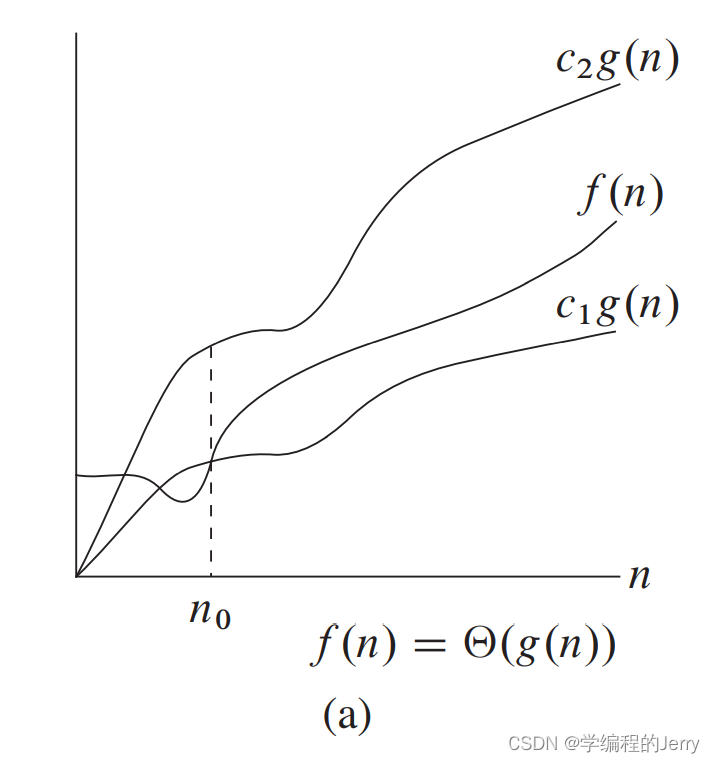
在n > n0时,因为f(n)一直被夹在c1g(n)和c2g(n)之间,f(n)在一个常量因子内等于g(n),因此我们称g(n)为f(n)的一个渐近紧确界(asymptotically tight bound)。
2、要求
θ(g(n))的定义要求每个成员f(n) ∈ θ(g(n))均渐近非负,即f(n)非负(渐近正函数就是对所有足够大的n均为正的函数)。
3、举个例子
我们要证明
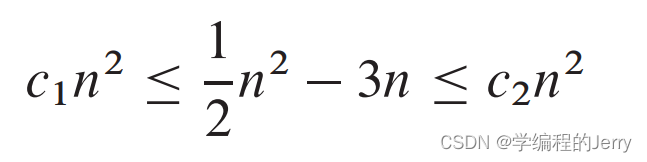
同除n^2得:
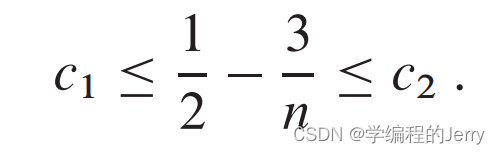
可得c2>=1/2,当no >= 7时,c1<=1/14,因此得证。
二、O记号
1、概念
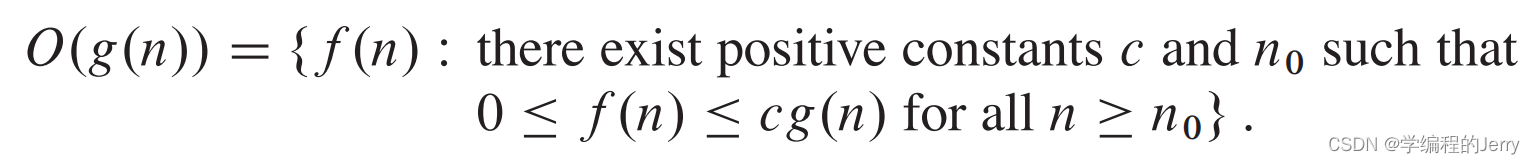
如何理解?相当于半个θ,只是用于描述上界,下界为0
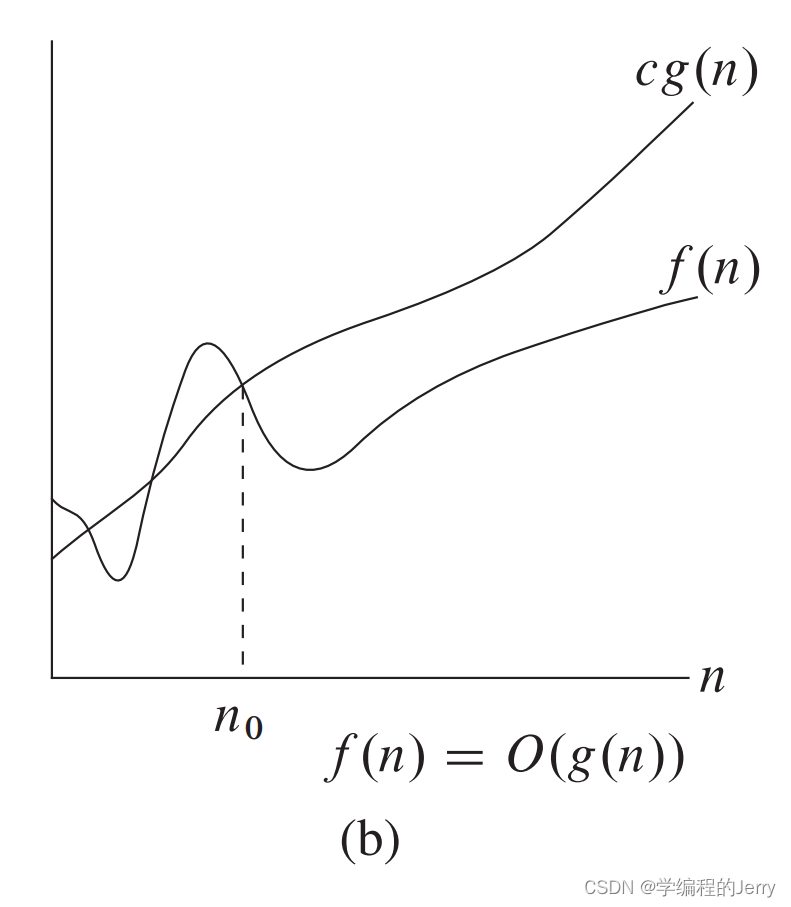
2、应用
往往用于描述算法的最坏情况。
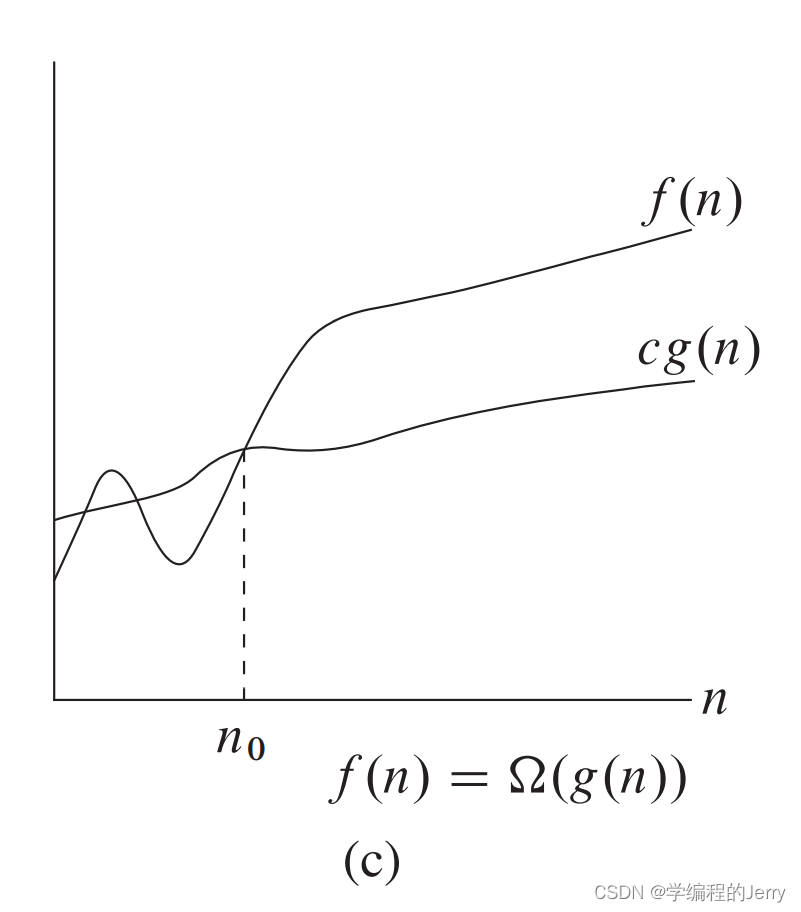
三、Ω记号
1、概念
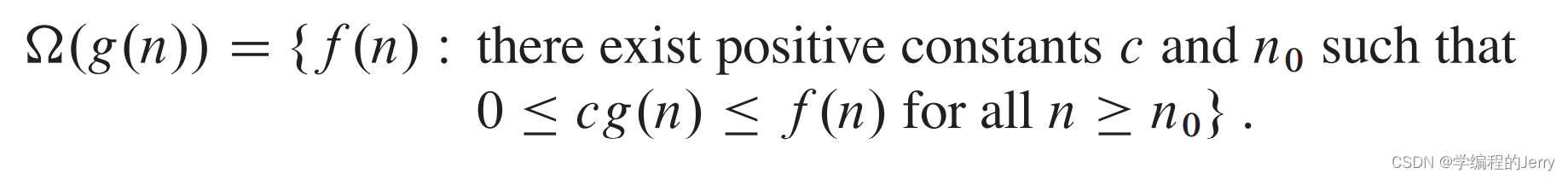
如何理解?
相当于半个θ,只是用于描述下界。
2、应用
往往用于描述算法的最好情况。
三、o记号
1、概念:
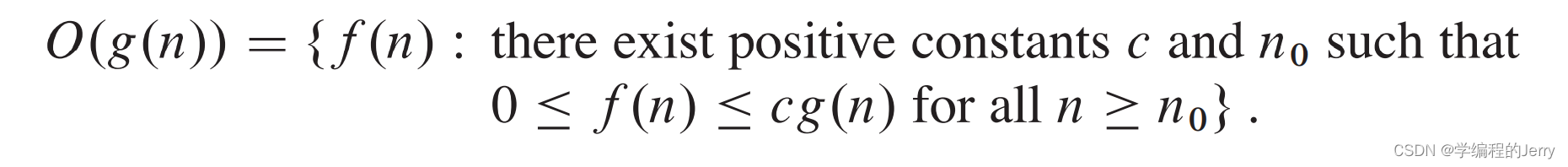
如何理解?
o记号和之前O记号定义类似,但主要的区别是在f(n)=O(g(n))中, 界0<=f(n)<=cg(n)对某个常量c成立,但是在f(n)=o(g(n))中, 界0<=f(n)<cg(n)对所有常量c>0成立,直观来看,当n无限大的时候,情况如下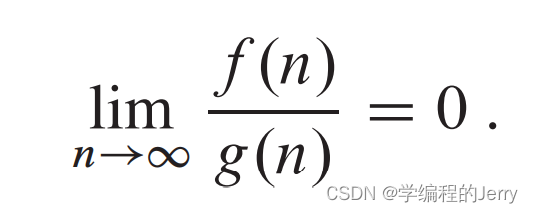
四、ω记号
1、概念
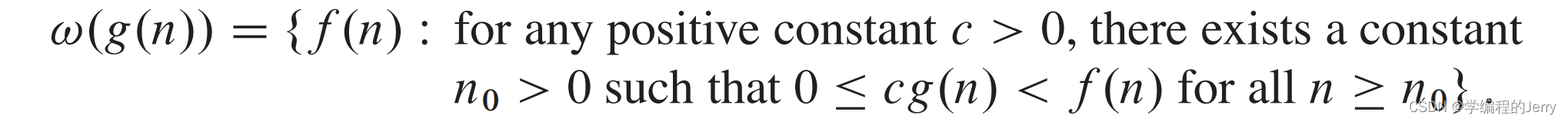
如何理解?
f(n)=ω(g(n))中 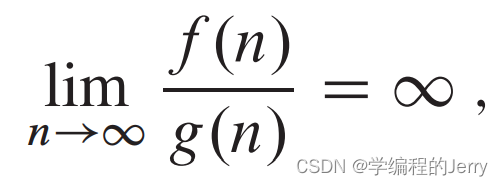
五、一些性质
1、传递性:
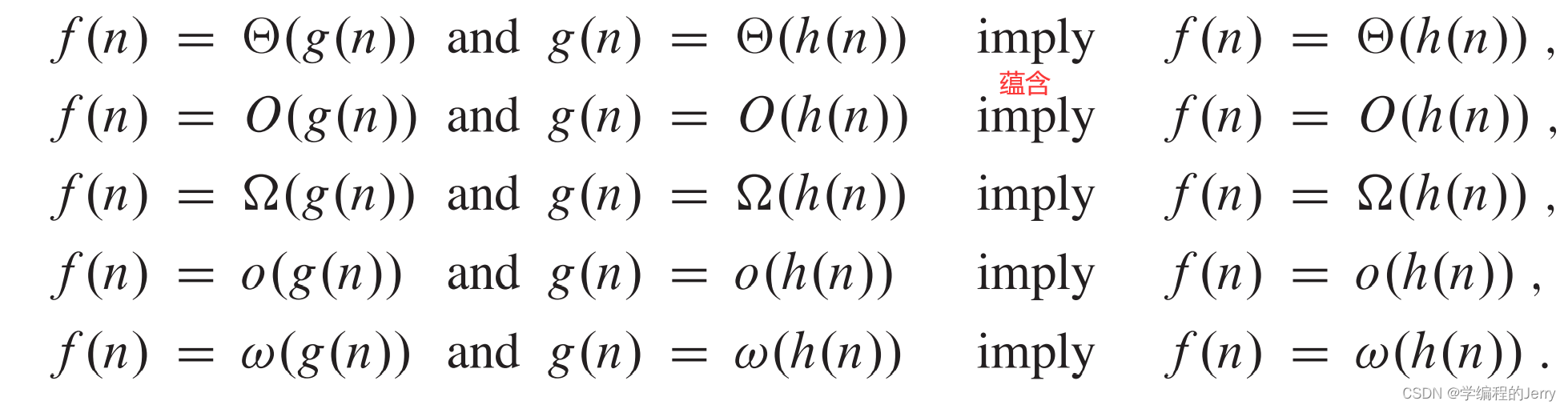
2、自反性
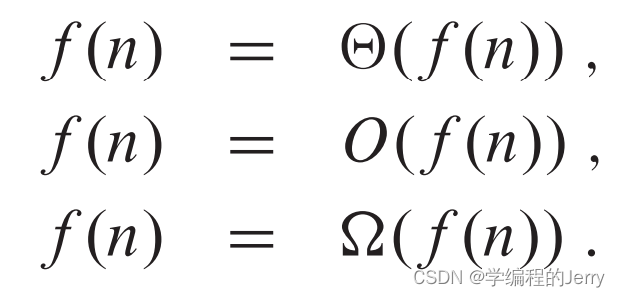
3、对称性

4、转置对称性
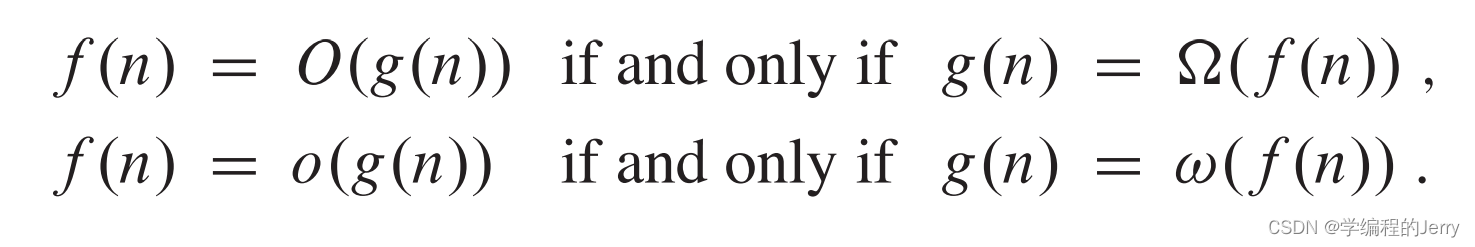
5、类比,将函数之间比较类比于实数之间的比较

边栏推荐
猜你喜欢
随机推荐
test3
idea使用jdbc对数据库进行增删改查,以及使用懒汉方式实现单例模式
DOM —— 事件对象
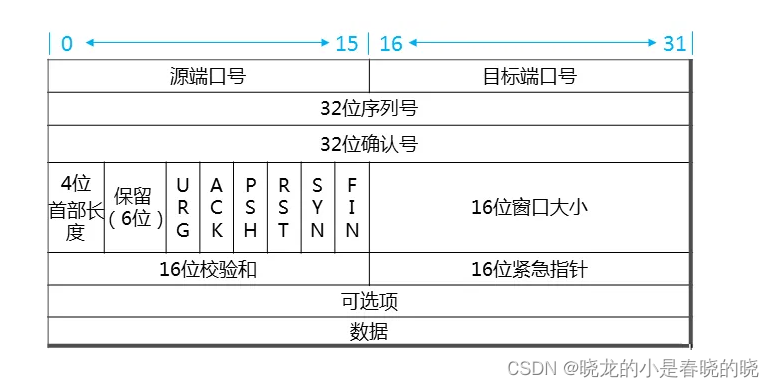
【网络参考模型】
网络运维系列:远程服务器登录、配置与管理
事件对象,事件流(事件冒泡和事件捕获)、事件委托、L0和L2注册等相关概念及用法
【交换机端口安全技术 】
详解C语言中的位操作运算符可以怎么用?
双亲委派机制
golang八股文整理(持续搬运)
2022-07-18 第五小组 瞒春 学习笔记
有效的括号【暴力、分支判断、哈希表】
APP版本更新通知流程测试要点
为什么float4个字节比long8个字节所表示的数值范围广
DOM - page rendering process
nodejs 的下载安装与环境配置
makefile——杂项
IDEA如何进行远程Debug
加载事件的用法
【滤波器】最小均方(LMS)自适应滤波器
![[Fault Diagnosis] Weak Fault Diagnosis of Fan Bearing Based on PSO_VMD_MCKD Method](/img/43/719caffc79950edd18719ad0ba3aff.jpg)