Yugu p1020 missile interception (binary search)

subject

In order to defend against the missile attack of the enemy , Developing a missile interception system . But there's a flaw in this interceptor system ： Although its first shell can reach any height , But in the future, each shell can not be higher than the height of the previous one . One day , The radar caught the enemy's missiles coming . Because the system is still in the trial stage , So there's only one system , So it may not be possible to intercept all missiles .

Enter the Missile Altitude in turn （ The altitude data given by the radar is \le 50000≤50000 The positive integer ）, Calculate how many missiles this system can intercept at most , If you want to intercept all missiles, at least how many of these missile interception systems should be equipped .

Input format

1 That's ok , Several integers （ Number \le 100000≤100000）

NOIP The data scale of the original question does not exceed 2000.

Output format

2 That's ok , One integer per row , The first number shows how many missiles the system can intercept at most , The second number indicates the minimum number of such missile interception systems to be equipped if all missiles are to be intercepted .

sample input

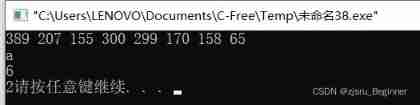
389 207 155 300 299 170 158 65

sample output

6
2

Design thinking

This question requires a non rising sequence length and a rising sequence length , Mainly used lower_bound And upper_bound To find out , First create an initial length of 1 Of len1 and len2,d1[1] and d2[1], As in the example above , First the 389 Add to an array , Compare again 389 And the next number 207, obviously 207 smaller , And add it to the array , Continue back until the number 300 when , Cannot be directly added to the array , You must replace the first one in the array that is less than 300 The number of , namely 207. Add and replace many times , It finds out the maximum number of missiles that can be intercepted and the minimum system to be equipped .

The following description follows lower_bound And upper_bound Usage of ：

Both of these functions can only be used for ascending sequences , The following example ：

int main()
{
	int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12};
 
  cout << (lower_bound(a, a + 12, 4) - a) << endl; // Output 3 
  cout << (upper_bound(a, a + 12, 4) - a) << endl; // Output 4 
  
}

If the sequence is descending ：

	int a[] = {4, 4, 4, 3, 3, 3, 2, 2, 2, 1, 1, 1};
  cout << (lower_bound(a, a + 12, 4) - a) << endl; // Output 12 
  cout << (upper_bound(a, a + 12, 4) - a) << endl; // Output 12
  cout << (lower_bound(a, a + 12, 1) - a) << endl; //  Output 0 
  cout << (upper_bound(a, a + 12, 1) - a) << endl; //  Output 0

The code is as follows ：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N], d1[N], d2[N], n;
int main() {
	while (cin >> a[++n]); n--;	
	int len1 = 1, len2 = 1;		// The initial length is 1
	d1[1] = a[1];		// Used to calculate the length of Non rising sequence 
	d2[1] = a[1];		// Used to find the length of ascending sequence 
	for (int i=2; i<=n; i++) {		// from a[2] Start enumerating each number 
		if (d1[len1] >= a[i]) d1[++len1] = a[i];		// If you meet the requirements and don't rise, join d1
		else {		// Otherwise, use a[i] Replace d1 One of the numbers 
			int p1 = upper_bound(d1 + 1, d1 + 1 + len1, a[i], greater<int>()) - d1;
			d1[p1] = a[i]; 
		}
		if (d2[len2] < a[i]) d2[++len2] = a[i];		
		else {
			int p2 = lower_bound(d2 + 1, d2 + 1 + len2, a[i]) - d2;
			d2[p2] = a[i];
		}
	}
	cout << len1 << endl << len2;		
	return 0;		
}
        

Running results ：

big data 201 tyx