论文理解：“Gradient-enhanced physics-informed neural networks for forwardand inverse PDE problems“

译：梯度增强物理信息神经网络用于正向和反向偏微分方程问题

-- Computer methods in applied mechanics engineering -- 2022

---

目录

一、引言

二、方法

2.1、PINN

2.2、gPINNs

2.3、基于残差自适应细化(RAR)的gPINN算法

三、实验

3.1、函数逼近

3.2、PDE正问题

3.3、PDE逆问题

3.4、通过RAR增强gPINN

3.5、gPINN的计算成本

---

一、引言

        物理信息神经网络(PINNs)通过使用自动微分将PDE嵌入神经网络的损失中来求解PDE，而且解决反PDE问题就像解决正向问题一样容易。但是提高PINN的精度和效率是一个有待解决的问题。

        PINN使用PDE残差作为每个PDE的相应损失，尚未注意到PDE的其他类型的损失。作者想到如果PDE残差为零，PDE残差的梯度也应该为零。

        因此作者提出了梯度增强的PINN (gPINN)，它利用一种新型的损失函数，利用PDE残差的梯度信息来提高PINN的精度。

二、方法

2.1、PINN

        首先回忆一下PINN怎么解决正向和逆向问题。

考虑由定义域Ω上定义的参数λ参数化的解u(x, t)的下列偏微分方程：

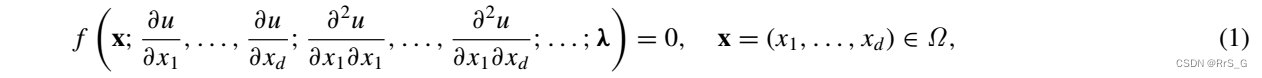
边界条件：

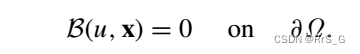
简单来说就是用神经网络近似u(x)优化下列损失即可解决正向问题：

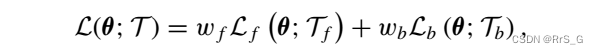
其中：

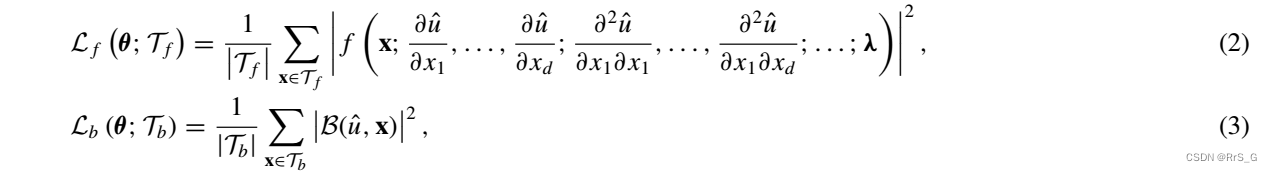
(2)式使用的是定义域内部的点，(3)式是边界点。

而对于逆问题，λ就未知了，同时又多了对u的已知量，因此损失变成：

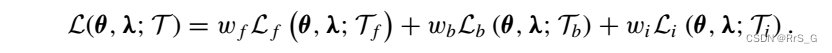
即多了一项：

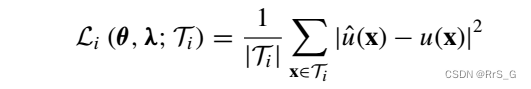
对于怎样获取参数λ：解决正问题时，优化损失得到网络参数即可。但是解决逆问题时，要把pde的参数λ也设置成变量去更新，即优化逆问题的损失同时得到网络参数和pde的参数λ。

2.2、gPINNs

        引言中提到f的导数也是零。即:

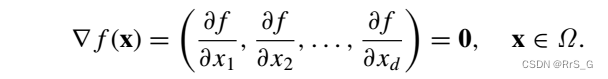
损失在PINN的基础上变为：

其中：

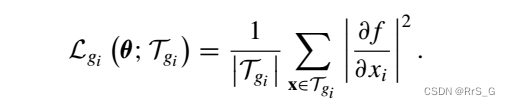
注意，本文的和是一样的，但可以不一样。

通过后面的实验结果能发现，gPINN提高了u的预测解的精度，并且需要更少的训练点。gPINN的一个动机是PINN的PDE残差通常在零附近波动，惩罚残差的斜率可以减少波动，使残差更接近零。

2.3、基于残差自适应细化(RAR)的gPINN算法

具体算法如下：

三、实验

        下面是基于本文的网络做的各种实验，只选取部分实验做参考。

原文代码：https://github.com/lu-group/gpinn

3.1、函数逼近

        作者首先用一个函数逼近的例子来证明添加梯度信息的有效性。考虑下面的函数

 训练点均匀采样，损失如下：

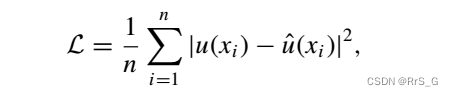
还考虑以下带有额外梯度的损失函数：

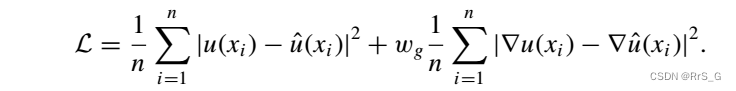
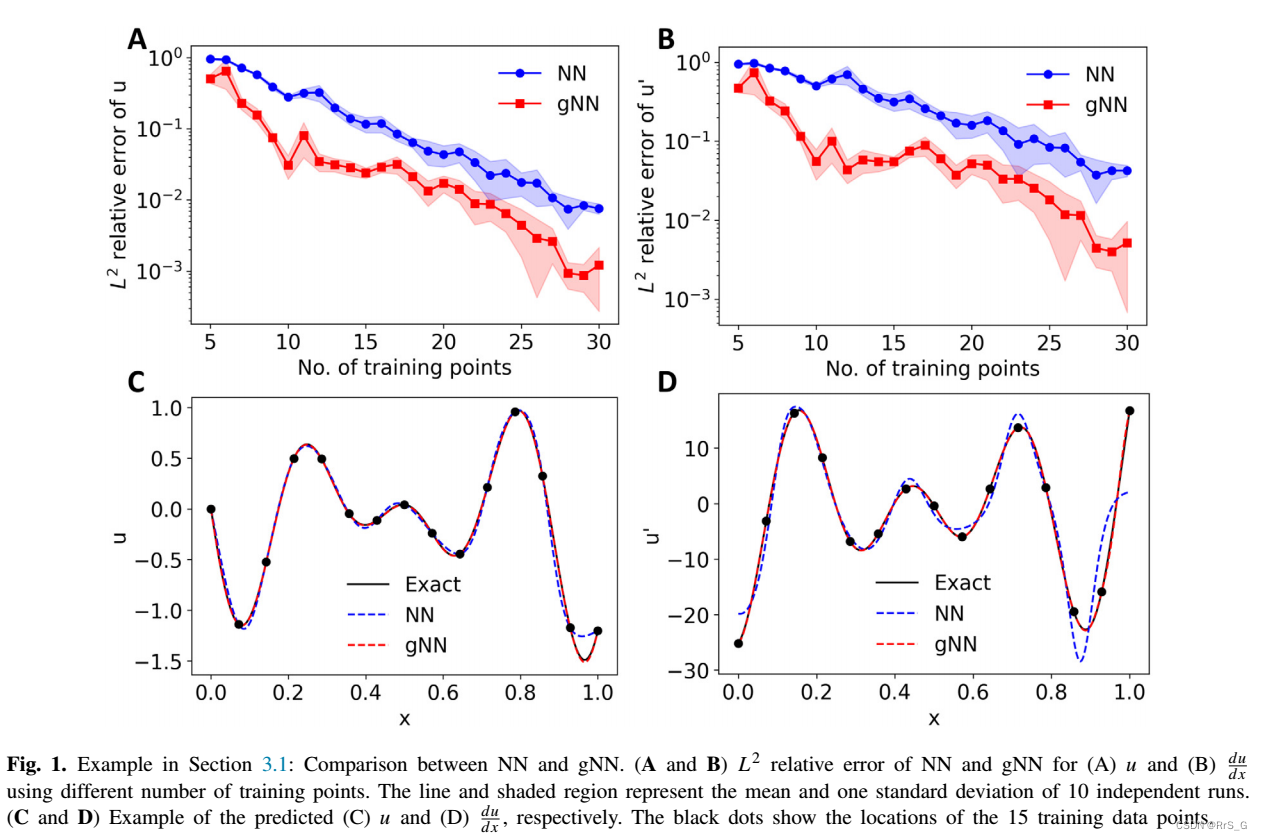
结果如下：

3.2、PDE正问题

        下面将gPINN应用于偏微分方程的求解，以扩散反应方程为例，方程如下：

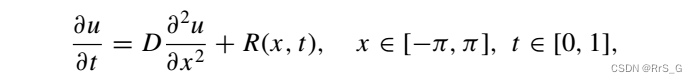
式中，u为溶质浓度，D = 1为扩散系数，R为化学反应

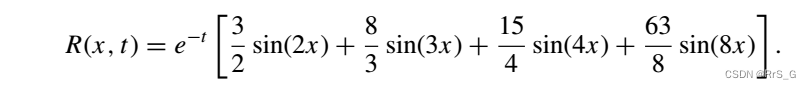
初始条件和边界条件如下:

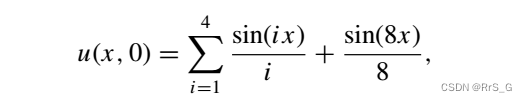
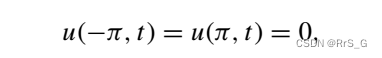
解析解为：

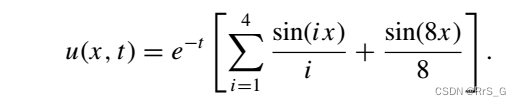
作者选择合适的解代理来自动满足初始条件和边界条件(损失函数就不用考虑这两项了):

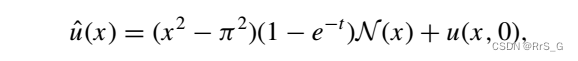
其中N(x)是神经网络。这里有两个梯度的损失项(对x和对t的导数损失)，总的损失函数是

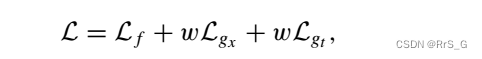
结果如下：

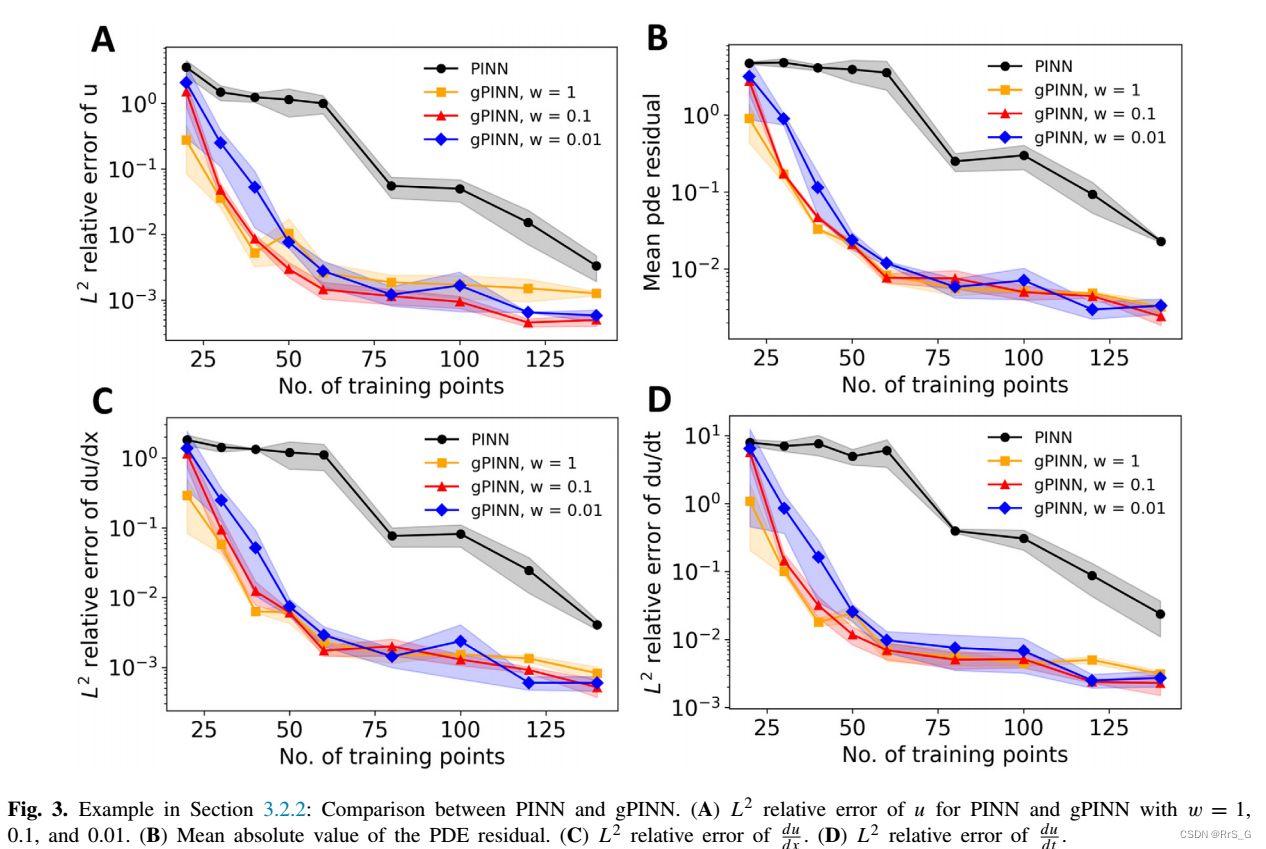
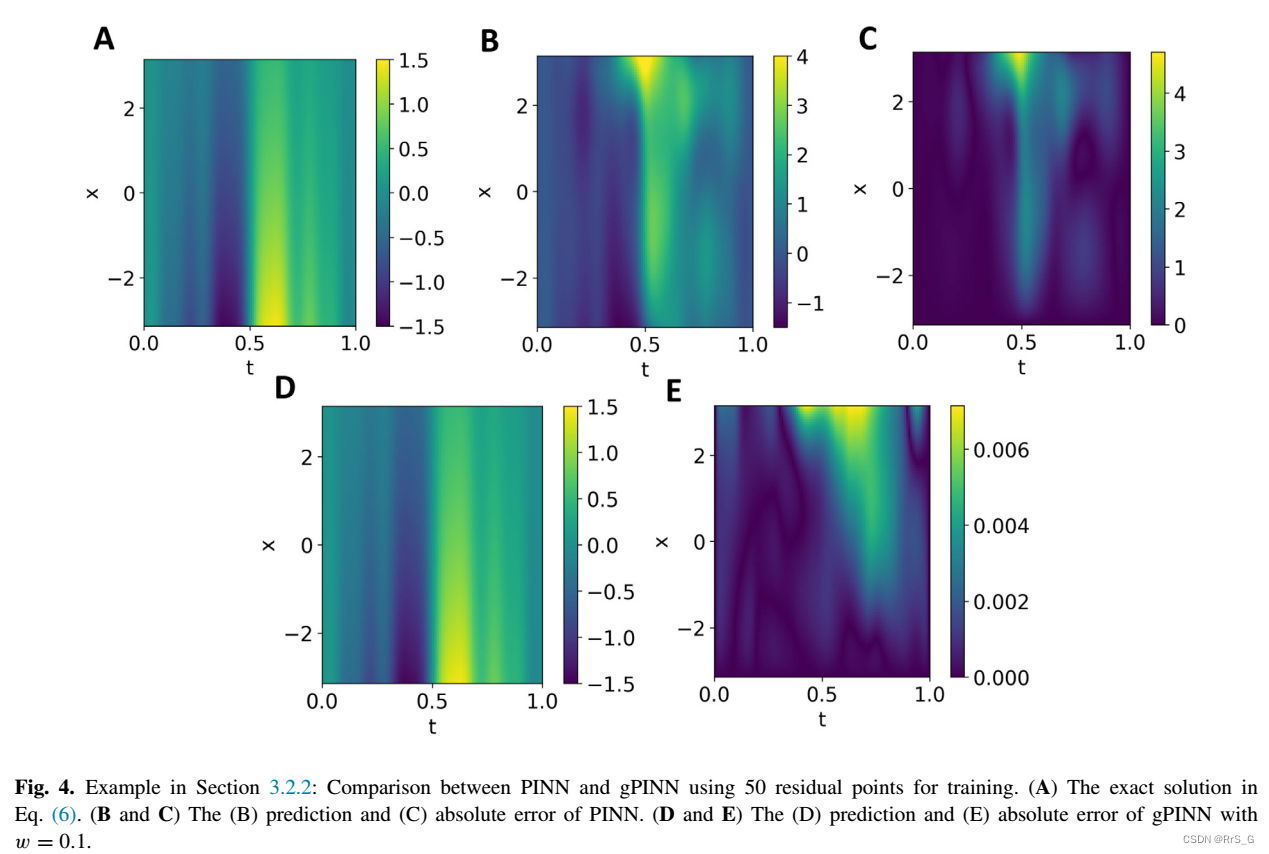
3.3、PDE逆问题

        这里考虑Brinkman-Forchheimer模型的有效粘度和渗透率。Brinkman-Forchheimer模型可以看作是扩展的达西定律，用于描述有壁边界的多孔介质流动:

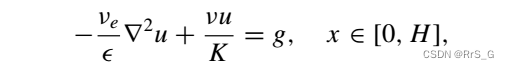
其中，解u为流体速度，g为外力，v为流体的运动粘度，ε为多孔介质的孔隙率，K为渗透率。有效粘度与孔隙结构有关，难以确定。设无滑移边界条件，即u(0) = u(1) = 0。这个问题的解析解是

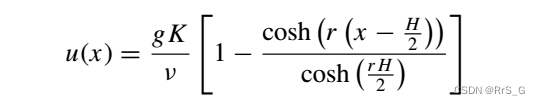
其中。 

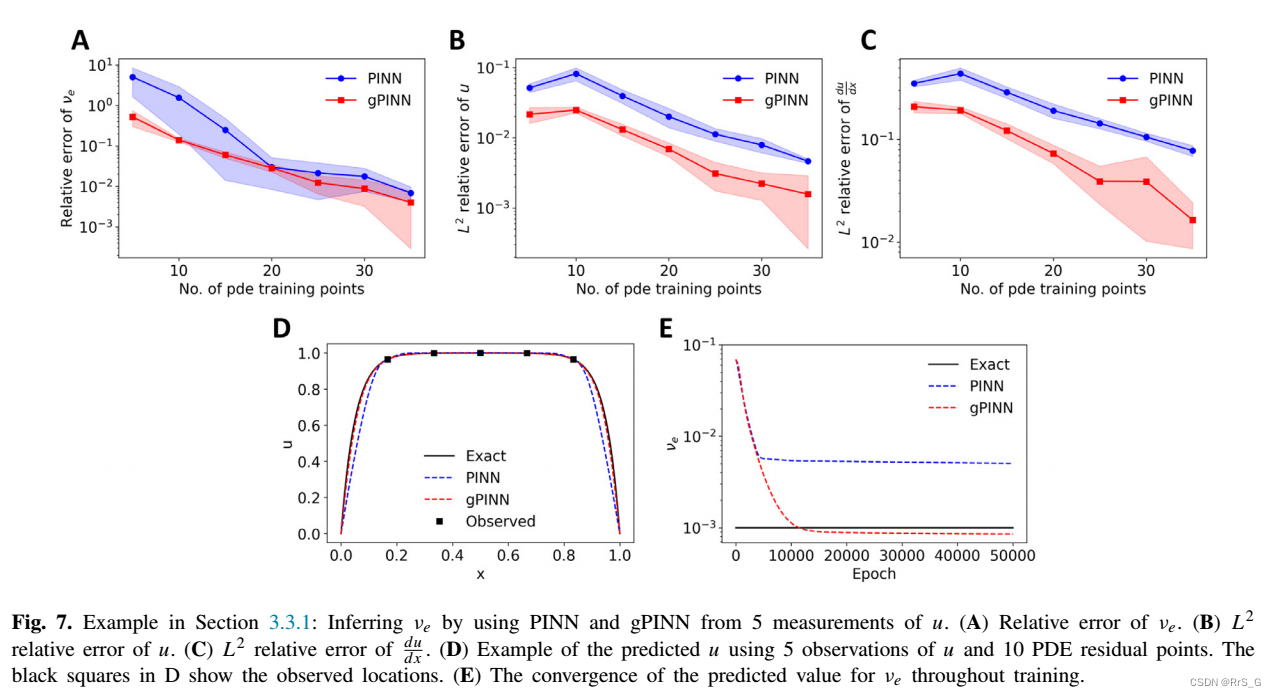
明确来说，这个例子的目标是推断，同时优化网络的参数和的值。作者只在5个传感器位置收集了速度u的数据测量。

结果如下：

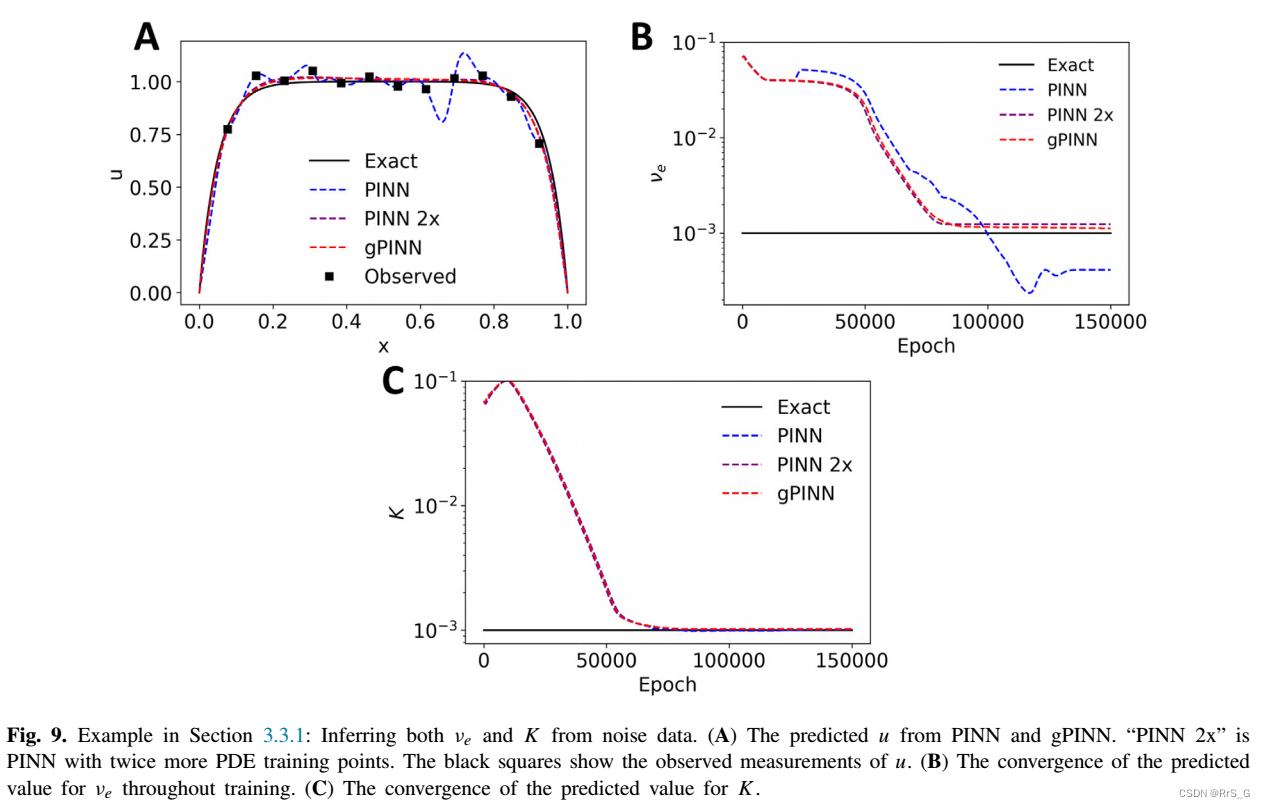
接下来，作者将高斯噪声(均值0和标准差0.05)添加到观测值中，并使用12次u的测量值推断和K。结果如下：

注：不同于这个例子，如果PDE逆问题要求的方程参数是一个函数而不是一个常数的话，可以用另外一个网络去近似这个参数。具体参考原文PDE逆问题第二个例子。

3.4、通过RAR增强gPINN

        为了进一步提高gPINN求解刚性PDEs的精度和训练效率，在训练过程中应用RAR自适应地改善残差点的分布。

结果如下：

3.5、gPINN的计算成本

        gPINN相对于PINN的相对计算代价(下表中第二行的值)为gPINN的训练时间除以PINN的训练时间。

注：3.4和3.5的方程相同，没有表示出来。

最后，再附上原文代码：https://github.com/lu-group/gpinn