当前位置:网站首页>7 RSA Cryptosystem
7 RSA Cryptosystem
2022-07-04 17:33:00 【Grilled little fat sheep with charcoal...】
RSA introduction
RSA Cryptographic schemes are sometimes called Rivest-Shamir-Adleman Algorithm , It is currently the most widely used asymmetric cryptographic scheme .RSA stay USA( Except for other countries ) The duration of the patent lasts until 2000 year .
RSA Widely applied , But it is often used in practice :
- Encryption of small pieces of data , Especially for key transmission
- digital signature , such as Internet Digital certificate on .
Be careful :RSA Encryption is not intended to replace symmetric passwords , And it's better than things like AES Your password is much slower . This is mainly because RSA( Or other public key algorithms ) Many calculations are involved in the implementation . therefore , The main purpose of encryption features is to securely exchange keys of symmetric passwords ( Key transmission ). actually ,RSA Usually similar to AES Used together with symmetric passwords , Among them, the symmetric password is really used to encrypt a large amount of data .
RSA The underlying one-way function is the integer factorization problem : Multiplication of two large primes is very simple in calculation ( People can do it with pen and paper ), But it is very difficult to factorize the product result .
encryption and decryption
RSA Both encryption and decryption are in the integer ring Z n Z_n Zn To finish the , Modular computing plays a central role .
Suppose you use RSA Encrypt plaintext x x x, And it means x x x The bit string of is Z n = 0 , 1 , . . , n − 1 Z_n = {0,1,..,n-1} Zn=0,1,..,n−1 Internal elements . So plaintext x x x The binary value represented must be less than n n n. For ciphertext , This principle also holds . Encryption with public key and decryption with key can be expressed as :
RSA encryption : Given public key ( n , e ) = k p u b (n, e) = k_{pub} (n,e)=kpub And plaintext x x x, Then the encryption function is : y = e k p u b ( x ) ≡ x e m o d n (1) y = e_{k_{pub}}(x) \equiv x^e mod n \tag 1 y=ekpub(x)≡xemodn(1) among x , y ∈ Z n x,y \in Z_n x,y∈Zn
RSA Decrypt : Given private key d = k p r d = k_{pr} d=kpr And ciphertext y y y, Then the decryption function is : x = d k p r ( y ) ≡ y d m o d n (2) x = d_{k_{pr}}(y) \equiv y^d mod n \tag 2 x=dkpr(y)≡ydmodn(2) among x , y ∈ Z n x,y \in Z_n x,y∈Zn
In the actual x , y , n x, y, n x,y,n and d d d Are very long numbers , Usually it is 1024 Bit or longer . value e Sometimes called crypto index or public index ; Private key d Sometimes called decryption index or secret index . If Alice I want to transmit an encrypted message to Bob, She needs to have Bob The public key (n,e), and Bob Will use his own private key d To decrypt . The next summary will discuss how to generate these three important parameters d,e and n. Now we can discuss RSA Some requirements of cryptosystem ;
- Because the attacker can get the public key ( n , e ) = k p u b (n, e) = k_{pub} (n,e)=kpub, therefore , For a given public key value e e e and n n n, Determine private key d d d In calculation
It must be infeasible . - Due to plaintext x x x It only depends on the modulus n n n Size , So once RSA The number of bits encrypted cannot exceed l l l, among l l l refer to n n n Bit length of .
- Calculation x e m o d n x^e mod n xemodn( That is, encryption ) and y d m o d n y^d mod n ydmodn( Decryption ) It should be relatively simple . This means that we need a method that can quickly calculate the exponent of long integers .
- Given a n n n It should correspond to many keys / Public key for , otherwise , The attacker can launch a brute force attack ( The fact proved that , This requirement is easy to meet ).
Key generation and correctness verification
A salient feature of all asymmetric schemes is , They all have a handshake stage to calculate the public key and private key . Key generation depends on the public key scheme , So it's very complicated . Here are RSA The steps involved in computing public and private keys in cryptosystems .
RSA Key generation :
Output : Public key : k p u b k_{pub} kpub = (n, e) And a private key : k p r = ( d ) k_{pr} = (d) kpr=(d)
- Choose two prime numbers p p p and q q q.
- Calculation n = p ∗ q n = p * q n=p∗q.
- Calculation Φ ( n ) = ( p − 1 ) ∗ ( q − 1 ) \Phi(n) = (p - 1)*(q - 1) Φ(n)=(p−1)∗(q−1).
- Select the public index that meets the following conditions e ∈ { 1 , 2 , . . . . . , Φ ( n ) − 1 } e \in \{1, 2, ....., \Phi(n) - 1\} e∈{ 1,2,.....,Φ(n)−1}: g c d ( e , Φ ( n ) ) = 1 . gcd(e, \Phi(n)) = 1. gcd(e,Φ(n))=1.
- Calculate the private key that meets the following conditions d d d: d ∗ e ≡ 1 m o d Φ ( n ) d*e \equiv 1 mod \Phi(n) d∗e≡1modΦ(n)
step 4 In the request g c d ( e , Φ ( n ) ) = 1 gcd(e, \Phi(n)) = 1 gcd(e,Φ(n))=1 It's to make sure that e e e The existence module of the inverse element of Φ ( n ) \Phi(n) Φ(n), So the private key d d d Always there .
There are two important parts in key generation : Step of selecting two large primes 1 And the steps of calculating the public and private keys 4 and 5. step 1 The generation of prime numbers in is very complex . Using the extended Euclidean algorithm (EEA) The key can be calculated immediately d d d and e e e. In the actual , People usually start with 0 < e < Φ ( n ) 0 < e < \Phi(n) 0<e<Φ(n) Select a public parameter in the range , And e e e The value of must meet the condition g c d ( e , Φ ( n ) ) = 1 gcd(e, \Phi(n))=1 gcd(e,Φ(n))=1. The input parameter n n n and e e e For Euclidean algorithm (EEA) You can get the following relationship : g c d ( Φ ( n ) , e ) = s ⋅ Φ ( n ) + t ⋅ e gcd(\Phi(n), e) = s\cdot\Phi(n) + t\cdot e gcd(Φ(n),e)=s⋅Φ(n)+t⋅e
If g c d ( Φ ( n ) , e ) = 1 gcd(\Phi(n), e) = 1 gcd(Φ(n),e)=1, be e e e Is a valid public key . Parameters obtained by using the extended Euclidean algorithm t t t That is to say e e e Inverse element , So there is : d = t m o d Φ ( n ) . d = t mod \Phi(n). d=tmodΦ(n).
Example :Alice Want to send an encrypted message to Bob. First ,Bob Execution steps 1~5 Calculation RSA Parameters , And send his public key to Alice. Alice Then send the message (x=4) encryption , And will get the ciphertext y Send to Bob. Last ,Bob Decrypt with his own private key y. Be careful : Both private key index and public key index meet the conditions e ∗ d = 3 ∗ 7 ≡ 1 m o d Φ ( n ) e*d = 3*7 \equiv 1 mod\Phi(n) e∗d=3∗7≡1modΦ(n)
Be careful : Both private key index and public key index meet the conditions e ∗ d = 3 ∗ 7 ≡ 1 m o d Φ ( n ) e*d = 3*7 \equiv 1 mod\Phi(n) e∗d=3∗7≡1modΦ(n)
In practice RSA The parameters will be very, very large RSA modulus n Should be at least 1024 Bit length , This makes p and q The bit length of is at least 512. Here is the bit length 1024 Of RSA Examples of parameters .
p = E O D F D 2 C 2. A 288 A C E B C 705 E F A B 30 E 4447541 A 8 C 5447 A 37185 C S A 9 C B 98389 C E 4 D E 19199 A A 3069 B 404 F D 98 C 801568 C B 9170 E B 712 B F 10 B 4955 C E 9 C 9 D C 8 C E 6855 C 612 3 h p=EODFD2C2.A288ACEBC705EFAB30E4447541A8C5447A37185CSA9CB98389CE4DE19199AA3069B404FD98C801568CB9170EB712BF10B4955CE9C9DC8CE6855C6123_h p=EODFD2C2.A288ACEBC705EFAB30E4447541A8C5447A37185CSA9CB98389CE4DE19199AA3069B404FD98C801568CB9170EB712BF10B4955CE9C9DC8CE6855C6123h
q = E B E O F C F 21866 F D 9 A 9 F O D 72 F 7994875 A 8 D 92 E 67 A E E 4 B 515136 B 2 A 778 A 8048 B 149828 A E A 30 B D O B A 34 B 977982 A 3 D 42168 F 594 C A 99 F 3981 D D A B F A B 2369 F 22964011 5 h q=EBEOFCF21866FD9A9FOD72F7994875A8D92E67AEE4B515136B2A778A8048B149828AEA30BDOBA34B977982A3D42168F594CA99F3981DDABFAB2369F229640115_h q=EBEOFCF21866FD9A9FOD72F7994875A8D92E67AEE4B515136B2A778A8048B149828AEA30BDOBA34B977982A3D42168F594CA99F3981DDABFAB2369F229640115h
n = C F 33188211 F D F 6052 B D B B 1 A 37235 E O A B B 5978 A 45 C 71 F D 381491 A D 12 F C 76 D A 0544 C 47568 A C 83 D 855 D 47 C A 8 D 8 A 779579 A B 72 E 635 D O B 0 A A A C 22 D 28341 E 998 E 90 F 82122 A 2 C 06090 F 43 A 37 E 0203 C 2 B 72 E 401 F D 06890 E C 8 E A D 4 F 07 E 686 E 906 F O 1 B 2468 A E 7 B 30 C B D 670255 C 1 F E D E 1 A 2762 C F 4392 C 0759499 C C O A B E C F F 008728 D 9 A 11 A D F h n=CF33188211FDF6052BDBB1A37235EOABB5978A45C71FD381491AD12FC76DA0544C47568AC83D855D47CA8D8A779579AB72E635DOB0AAAC22D28341E998E90F82122A2C06090F43A37E0203C2B72E401FD06890EC8EAD4F07E686E906FO1B2468AE7B30CBD670255C1FEDE1A2762CF4392C0759499CCOABECFF008728D9A11ADF_h n=CF33188211FDF6052BDBB1A37235EOABB5978A45C71FD381491AD12FC76DA0544C47568AC83D855D47CA8D8A779579AB72E635DOB0AAAC22D28341E998E90F82122A2C06090F43A37E0203C2B72E401FD06890EC8EAD4F07E686E906FO1B2468AE7B30CBD670255C1FEDE1A2762CF4392C0759499CCOABECFF008728D9A11ADFh
e = 40 B 028 E 1 E 4 C C F 07537643101 F F 72444 A O B E 1 D 7682 F 1 E D B 553 E 3 A B 4 F 6 D D 8293 C A 1945 D B 12 D 796 A E 9244 D 60565 C 2 E B 692 A 89 B 8881 D 58 D 278562 E D 60066 D D 8211 E 67315 C F 89857167206120405 B O 8 B 54 D 10 D 4 E C 4 E D 4253 C 75 F A 74098 F E 3 F 7 F B 751 F F 5121353 C 554391 E 114 C 85 B 5649725 E 9 B D 5685 D 6 C 9 C T E E D 8 E E 442366353 D C 39 , d = C 21 A 93 E E 75148 D 4 F B F D 77285 D 79 D 6768 C 58 E B F 283743 D 2889 A 395 F 266 C 78 F 4 A 28 E 86 F 545960 C 2 C E O 1 E B 8 A D 5246905163 B 28 D O B 8 B A A B B 959 C C 03 F 4 E C 499186168 A E 9 E D 6 D 88058898907 E 61 C T c C C C 584 D 65 D 801 C F E 32 D F C 983707 F 87 F 5 A A 6 A E 4 B 9 E 77 B 9 C E 630 E 2 C O D F 05841 B 5 E 4984 D 059435 D 7270 D 500514891 F 7 B 77 B 804 B E D 8 1 h e=40B028E1E4CCF07537643101FF72444AOBE1D7682F1EDB553E3AB4F6DD8293CA1945DB12D796AE9244D60565C2EB692A89B8881D58D278562ED60066DD8211E67315CF89857167206120405BO8B54D10D4EC4ED4253C75FA74098FE3F7FB751FF5121353C554391E114C85B5649725E9BD5685D6C9CTEED8EE442366353DC39,d=C21A93EE75148D4FBFD77285D79D6768C58EBF283743D2889A395F266C78F4A28E86F545960C2CEO1EB8AD5246905163B28DOB8BAABB959CC03F4EC499186168AE9ED6D88058898907E61CTcCCC584D65D801CFE32DFC983707F87F5AA6AE4B9E77B9CE630E2CODF05841B5E4984D059435D7270D500514891F7B77B804BED81_h e=40B028E1E4CCF07537643101FF72444AOBE1D7682F1EDB553E3AB4F6DD8293CA1945DB12D796AE9244D60565C2EB692A89B8881D58D278562ED60066DD8211E67315CF89857167206120405BO8B54D10D4EC4ED4253C75FA74098FE3F7FB751FF5121353C554391E114C85B5649725E9BD5685D6C9CTEED8EE442366353DC39,d=C21A93EE75148D4FBFD77285D79D6768C58EBF283743D2889A395F266C78F4A28E86F545960C2CEO1EB8AD5246905163B28DOB8BAABB959CC03F4EC499186168AE9ED6D88058898907E61CTcCCC584D65D801CFE32DFC983707F87F5AA6AE4B9E77B9CE630E2CODF05841B5E4984D059435D7270D500514891F7B77B804BED81h
Verification of correctness :
RSA The core : d k p r ( y ) = d k p r ( e k p u b ( x ) ) ≡ x e d ≡ x d e ≡ x m o d n (3) d_{k_{pr}}(y) = d_{k_{pr}}(e_{k_{pub}}(x)) \equiv {x^e}^d \equiv x^{de} \equiv x mod n \tag 3 dkpr(y)=dkpr(ekpub(x))≡xed≡xde≡xmodn(3) Let's prove that RSA The reason why the scheme is feasible .
prove : It needs to be proved that decryption is the inverse function of encryption , namely d k p r ( e k p u b ( x ) ) = x d_{k_{pr}}(e_{k_{pub}}(x)) = x dkpr(ekpub(x))=x. First, let's explain the construction rules of public key and private key : d ∗ e ≡ 1 m o d Φ ( n ) d*e \equiv 1 mod\Phi(n) d∗e≡1modΦ(n). Using the definition of modulo operator , This expression is equivalent to : d ∗ e ≡ 1 + t ∗ Φ ( n ) d*e \equiv 1 + t*\Phi(n) d∗e≡1+t∗Φ(n)
among t Is an integer . Bring this expression into the equation ( 3 ) (3) (3) Available in : d k p r ( y ) ≡ x d e ≡ x 1 + t ∗ Φ ( n ) ≡ x t ∗ Φ ( n ) ∗ x 1 ≡ ( x Φ ( n ) ) t ∗ x m o d n (4) d_{k_{pr}}(y) \equiv x^{de} \equiv x^{1+t*\Phi(n)} \equiv x^{t*\Phi(n)} * x^1 \equiv (x^{\Phi(n)})^t *x mod n \tag 4 dkpr(y)≡xde≡x1+t∗Φ(n)≡xt∗Φ(n)∗x1≡(xΦ(n))t∗xmodn(4)
That means we need to prove x ≡ ( x Φ ( n ) ) t ∗ x m o d n x \equiv (x^{\Phi(n)})^t *x mod n x≡(xΦ(n))t∗xmodn. According to Euler's theorem , I.e g c d ( x , n ) = 1 gcd( x, n )= 1 gcd(x,n)=1, Then there are 1 ≡ x Φ ( n ) m o d n 1 \equiv x^{\Phi(n)} mod n 1≡xΦ(n)modn, Get a small promotion immediately : 1 ≡ 1 t ≡ ( x Φ ( n ) ) t m o d n (5) 1\equiv 1^t \equiv (x^{\Phi(n)})^t mod n \tag 5 1≡1t≡(xΦ(n))tmodn(5)
among ,t For any integer . This proof process is discussed in two cases :
Case one : g c d ( x , n ) = 1 gcd(x,n)=1 gcd(x,n)=1
In this case, Euler's theorem holds , The equation 5 5 5 Insert 4 4 4, obtain : d k p r ≡ ( x Φ ( n ) ) t ∗ x ≡ 1 ∗ x ≡ x m o d n . Prove BI d_{k_{pr}} \equiv (x^{\Phi(n)})^t *x \equiv 1*x \equiv x mod n. Certificate completion dkpr≡(xΦ(n))t∗x≡1∗x≡xmodn. Prove BI
This part of the proof shows , To and RSA modulus n n n Plaintext value of Coprime x x x for , The decryption function is indeed the inverse of the encryption function .
The second case : g c d ( x , n ) = g c d ( x , p ⋅ q ) ≠ 1 gcd(x,n)= gcd(x, p·q)≠ 1 gcd(x,n)=gcd(x,p⋅q)=1
because p p p and q q q They are all prime numbers , You must have any of the following factors : x = r ∗ p or person x = s ∗ q x = r*p perhaps x = s*q x=r∗p or person x=s∗q
among r , s r,s r,s All are integers , And meet r < q and s < p r<q and s<p r<q and s<p. In order not to lose generality , hypothesis x = r ⋅ p x=r·p x=r⋅p, Then you can get g c d ( x , q ) = 1 gcd(x, q)=1 gcd(x,q)=1. The following form of Euler's theorem still holds : 1 ≡ 1 t ≡ ( x Φ ( q ) ) t m o d q 1\equiv 1^t \equiv (x^{\Phi(q)})^t mod q 1≡1t≡(xΦ(q))tmodq
among t For any positive integer . Let's see next ( x Φ ( n ) ) t (x^{\Phi(n)})^t (xΦ(n))t: ( x Φ ( n ) ) t ≡ ( x ( p − 1 ) ( q − 1 ) ) t ≡ ( ( x Φ ( q ) ) t ) p − 1 ≡ 1 p − 1 = 1 m o d q . (x^{\Phi(n)})^t \equiv (x^{(p-1)(q-1)})^t \equiv ((x^{\Phi(q)})^t)^{p-1} \equiv 1^{p-1} = 1 mod q. (xΦ(n))t≡(x(p−1)(q−1))t≡((xΦ(q))t)p−1≡1p−1=1modq.
Use the definition of modulo operators , This expression is equivalent to : ( x Φ ( n ) ) t = 1 + u ∗ q , (x^{\Phi(n)})^t = 1 + u*q, (xΦ(n))t=1+u∗q,
among , u u u Is any integer . Multiply this equation by x x x Available : x ∗ ( x Φ ( n ) ) t = x + x ∗ u ∗ q = x + ( r ∗ p ) ∗ u ∗ q = x + r ∗ u ∗ ( p ∗ q ) = x + r ∗ u ∗ n x*(x^{\Phi(n)})^t = x + x*u*q= x + (r*p)*u*q= x + r * u * (p*q)=x + r * u * n x∗(xΦ(n))t=x+x∗u∗q=x+(r∗p)∗u∗q=x+r∗u∗(p∗q)=x+r∗u∗n
namely x ∗ ( x Φ ( n ) ) t = x m o d n (6) namely x*(x^{\Phi(n)})^t = x mod n \tag 6 namely x∗(xΦ(n))t=xmodn(6)
Put the equation 6 6 6 Put it into the equation 4 4 4 You can get the desired result : d k p r = ( x Φ ( n ) ) t ∗ x ≡ x m o d n . Prove BI d_{k_{pr}} = (x^{\Phi(n)})^t*x\equiv x mod n. Certificate completion dkpr=(xΦ(n))t∗x≡xmodn. Prove BI
Reference material :《 In simple terms, cryptography 》–Christof Paar,Jan Pelzl Writing
边栏推荐
猜你喜欢
随机推荐
[Huawei HCIA continuous update] SDN and FVC
整理混乱的头文件,我用include what you use
Interpretation of data security governance capability evaluation framework 2.0, the fourth batch of DSG evaluation collection
7 RSA密码体制
PingCode 性能测试之负载测试实践
What are cache penetration, cache breakdown, and cache avalanche
补能的争议路线:快充会走向大一统吗?
Display opencv drawn pictures on MFC picture control control
DataKit——真正的统一可观测性 Agent
ble HCI 流控机制
R语言plotly可视化:plotly可视化互相重叠的直方图(historgram)、并在直方图的顶部边缘使用geom_rug函数添加边缘轴须图Marginal rug plots
Zebras are recognized as dogs, and the reason for AI's mistakes is found by Stanford
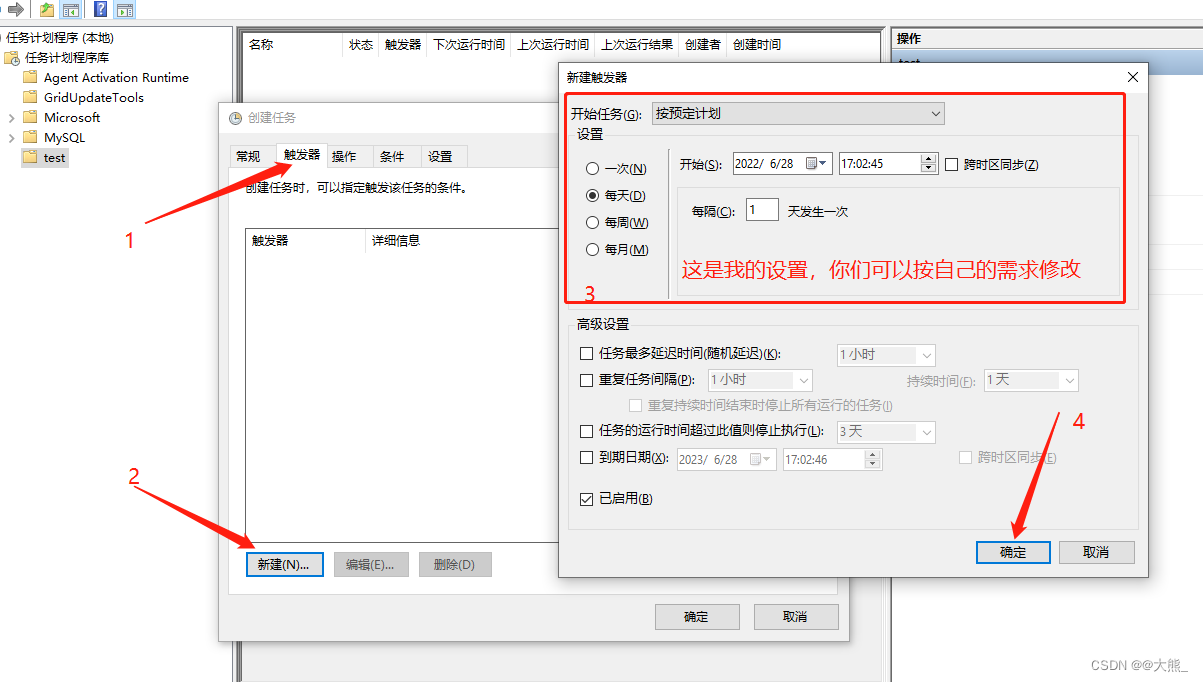
Using win10 scheduling task program to automatically run jar package at fixed time
Solution of dealer collaboration system in building materials industry: empowering enterprises to build core competitiveness
KS007基于JSP实现人个人博客系统
Which domestic cloud management platform manufacturer is good in 2022? Why?
Vb无法访问数据库stocks
[Acwing] 58周赛 4490. 染色
【HCIA持续更新】广域网技术
MD5加密的两种方式