当前位置:网站首页>[set theory] partition (partition | partition example | partition and equivalence relationship)
[set theory] partition (partition | partition example | partition and equivalence relationship)
2022-07-03 06:56:00 【Programmer community】
List of articles
- One 、 Divide
- Two 、 Partition example
- 3、 ... and 、 Partition and equivalence theorem
One 、 Divide
Divide :
Nonempty set
A
A
A ,
A
≠
∅
A \not= \varnothing
A=∅ ,
A
A
A One of the sets Divide yes Set family
A
\mathscr{A}
A ,
The Set family
A
\mathscr{A}
A Included in
A
A
A The power set of a set ,
A
⊆
P
(
A
)
\mathscr{A} \subseteq P(A)
A⊆P(A) , All elements in the set family belong to
A
A
A The power set of a set ;
Set family
A
\mathscr{A}
A The element in is aggregate , be called Partition ( Block ) , All the elements in the set are
A
A
A The elements in the collection ;
This set family
A
\mathscr{A}
A It has the following properties :
①
A
\mathscr{A}
A Every element in the set family is not empty
∅
∉
A
\varnothing \not\in \mathscr{A}
∅∈A
②
A
\mathscr{A}
A Any two elements in the set family ( Partition / aggregate ) It's disjoint
∀
x
,
y
(
x
,
y
∈
A
∧
x
≠
y
⇒
x
∩
y
=
∅
)
\forall x,y ( x,y \in \mathscr{A} \land x \not= y \Rightarrow x \cap y = \varnothing )
∀x,y(x,y∈A∧x=y⇒x∩y=∅)
③
A
\mathscr{A}
A Set all the elements in the family ( Partition / aggregate ) The union of is
A
A
A aggregate
⋃
A
=
A
\bigcup \mathscr{A} = A
⋃A=A
Quotient set is a division , The elements in this set family are set of equivalent classes ;
Quotient set reference : 【 Set theory 】 Equivalence class ( Concept of equivalence class | Examples of equivalence classes | Equivalence properties | Quotient set | Quotient set example ) Four 、 Quotient set
Two 、 Partition example
The whole book is
E
E
E ,
take
E
E
E Of
n
n
n individual Extraordinary Of True subset , The meaning of non trivial is that it is neither an empty set , It's not itself ;
∅
≠
A
1
,
A
2
,
⋯
,
A
n
⊂
E
\varnothing \not= A_1 , A_2, \cdots, A_n \subset E
∅=A1,A2,⋯,An⊂E
1. Divide 1 be based on
1
1
1 Elements
Set family
A
i
=
{
A
i
,
∼
A
i
}
\mathscr{A}_i = \{ A_i , \sim A_i \}
Ai={ Ai,∼Ai} ,
i
=
1
,
2
,
⋯
,
n
i = 1, 2, \cdots , n
i=1,2,⋯,n ,
A
i
\mathscr{A}_i
Ai The set family contains
A
i
A_i
Ai Set and its complement
∼
A
i
\sim A_i
∼Ai , This set family
A
i
\mathscr{A}_i
Ai Meet the three properties of the above division , It's a division ;
2. Divide 2 be based on
2
2
2 Elements
Set family
A
i
=
{
A
i
∩
A
j
,
∼
A
i
∩
A
j
,
A
i
∩
∼
A
j
,
∼
A
i
∩
∼
A
j
}
−
{
∅
}
\mathscr{A}_i = \{ A_i \cap A_j , \sim A_i \cap A_j , A_i \cap \sim A_j , \sim A_i \cap \sim A_j\} - \{ \varnothing \}
Ai={ Ai∩Aj,∼Ai∩Aj,Ai∩∼Aj,∼Ai∩∼Aj}−{ ∅} ,
i
,
j
=
1
,
2
,
⋯
,
n
∧
i
≠
j
i,j = 1, 2, \cdots , n \land i \not= j
i,j=1,2,⋯,n∧i=j
Understand according to the following Venn diagram :
A
i
∩
A
j
A_i \cap A_j
Ai∩Aj Corresponding area ①
∼
A
i
∩
A
j
\sim A_i \cap A_j
∼Ai∩Aj Corresponding area ③
A
i
∩
∼
A
j
A_i \cap \sim A_j
Ai∩∼Aj Corresponding area ②
∼
A
i
∩
∼
A
j
\sim A_i \cap \sim A_j
∼Ai∩∼Aj Corresponding area ④
- If
A
i
A_i
Ai And
A
j
A_j
Aj Disjoint , So the region ① It's an empty set , The partition class cannot be an empty set , At this point, you need to subtract the empty set , Corresponding
−
{
∅
}
-\{ \varnothing \}
−{ ∅}
3. Divide 3 be based on
3
3
3 Elements
Set family
A
i
j
k
=
{
A
i
∩
A
j
∩
A
k
,
A
i
∩
∼
A
j
∩
∼
A
k
,
∼
A
i
∩
A
j
∩
∼
A
k
,
∼
A
i
∩
∼
A
j
∩
A
k
,
∼
A
i
∩
∼
A
j
∩
∼
A
k
}
−
{
∅
}
\mathscr{A}_{ijk} = \{ A_i \cap A_j \cap A_k , A_i \cap \sim A_j \cap \sim A_k , \sim A_i \cap A_j \cap \sim A_k , \sim A_i \cap \sim A_j \cap A_k , \sim A_i \cap \sim A_j \cap \sim A_k\} - \{ \varnothing \}
Aijk={ Ai∩Aj∩Ak,Ai∩∼Aj∩∼Ak,∼Ai∩Aj∩∼Ak,∼Ai∩∼Aj∩Ak,∼Ai∩∼Aj∩∼Ak}−{ ∅}

4. Divide 4 be based on
n
n
n Elements
Set family
A
1
,
2
,
⋯
,
n
=
{
A
1
∩
A
2
∩
⋯
∩
A
n
,
A
1
∩
∼
A
2
∩
⋯
∩
∼
A
n
,
∼
A
1
∩
A
2
∩
⋯
∩
∼
A
n
,
⋮
∼
A
1
∩
∼
A
2
∩
⋯
∩
∼
A
n
}
−
{
∅
}
\begin{array}{lcl} \mathscr{A}_{1,2,\cdots,n} = \{ \\\\ A_1\cap A_2 \cap \cdots \cap A_n , \\\\ A_1\cap \sim A_2 \cap \cdots \cap \sim A_n , \\\\ \sim A_1\cap A_2 \cap \cdots \cap \sim A_n , \\\\ \vdots \\\\ \sim A_1\cap \sim A_2 \cap \cdots \cap \sim A_n \\\\ \} - \{ \varnothing \} \end{array}
A1,2,⋯,n={ A1∩A2∩⋯∩An,A1∩∼A2∩⋯∩∼An,∼A1∩A2∩⋯∩∼An,⋮∼A1∩∼A2∩⋯∩∼An}−{ ∅}
The rules :
A
1
A_1
A1 To
A
n
A_n
An Union ,
n
n
n individual
∼
A
1
\sim A_1
∼A1 To
∼
A
n
\sim A_n
∼An Union , Each of them is merged , Only one is not a complement ,
∼
A
1
\sim A_1
∼A1 To
∼
A
n
\sim A_n
∼An Union ;
3、 ... and 、 Partition and equivalence theorem
Partition and equivalence theorem :
Premise : aggregate
A
A
A Non empty ,
A
≠
∅
A \not= \varnothing
A=∅
R
R
R The relationship is
A
A
A Equivalence relations on sets , Can be derived ,
A
A
A Set about
R
R
R Quotient set of relation
A
/
R
A/R
A/R yes
A
A
A Division ;
R
yes
A
On
etc.
price
Turn off
system
⇒
A
/
R
yes
A
Of
draw
branch
R yes A Superior price relationship \Rightarrow A/R yes A Division
R yes A On etc. price Turn off system ⇒A/R yes A Of draw branch
Set family
A
\mathscr{A}
A yes
A
A
A Partition on set , Define a Binary relationship yes Same block relationship
R
A
R_{\mathscr{A}}
RA ,
The Same block relationship yes
A
A
A On the assembly Equivalence relation ,
The Same block relationship yes Divided by
A
\mathscr{A}
A Defined relationships ;
x
R
A
y
⇔
∃
z
(
z
∈
A
∧
x
∈
z
∧
y
∈
z
)
xR_{\mathscr{A}}y \Leftrightarrow \exist z ( z \in \mathscr{A} \land x \in z \land y \in z )
xRAy⇔∃z(z∈A∧x∈z∧y∈z)
边栏推荐
- Sorting out the core ideas of the pyramid principle
- 2022 East China Normal University postgraduate entrance examination machine test questions - detailed solution
- Summary of the design and implementation of the weapon system similar to the paladin of vitality
- DBNet:具有可微分二值化的实时场景文本检测
- php artisan
- Resttemplate configuration use
- dataworks自定义函数开发环境搭建
- Software testing assignment - the next day
- The essence of interview
- crontab定时任务
猜你喜欢

利用C#实现Pdf转图片

Software testing assignment - day 1
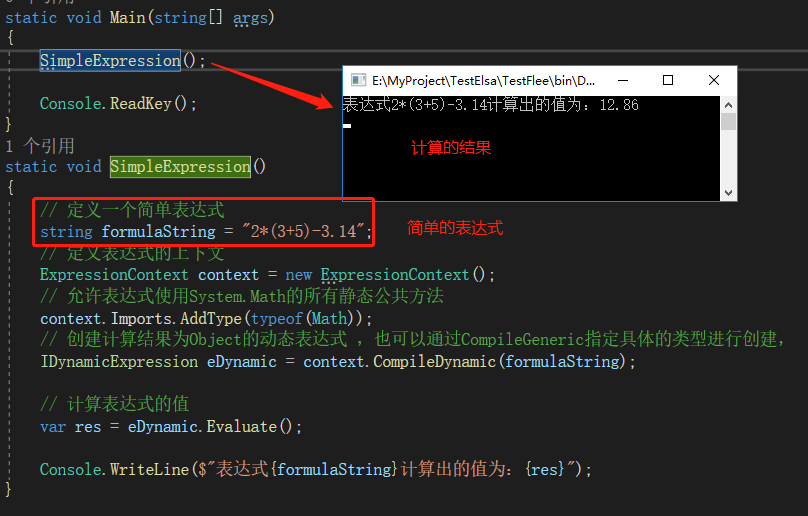
The dynamic analysis and calculation of expressions are really delicious for flee

Inno Setup 制作安装包
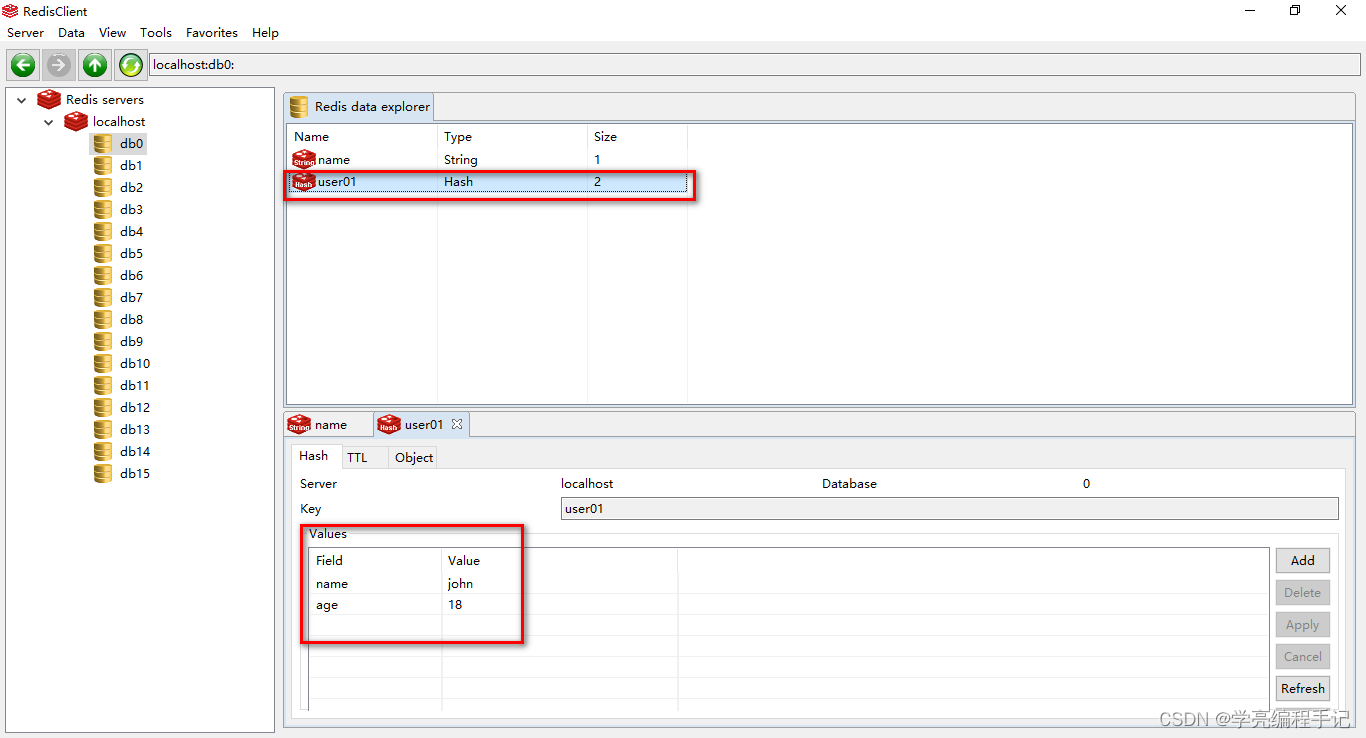
Golang operation redis: write and read hash type data
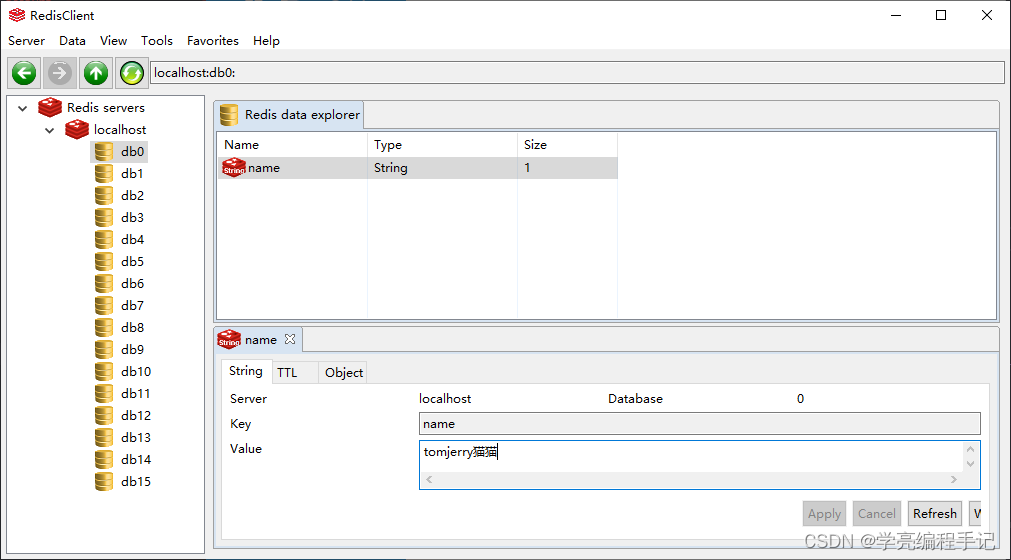
Golang operation redis: write and read kV data
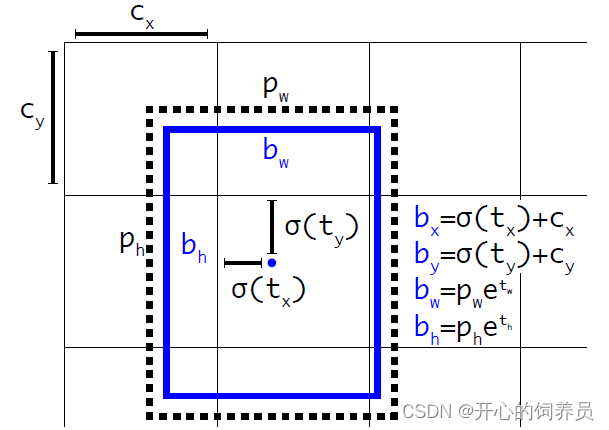
Yolov3 learning notes

(翻译)异步编程:Async/Await在ASP.NET中的介绍
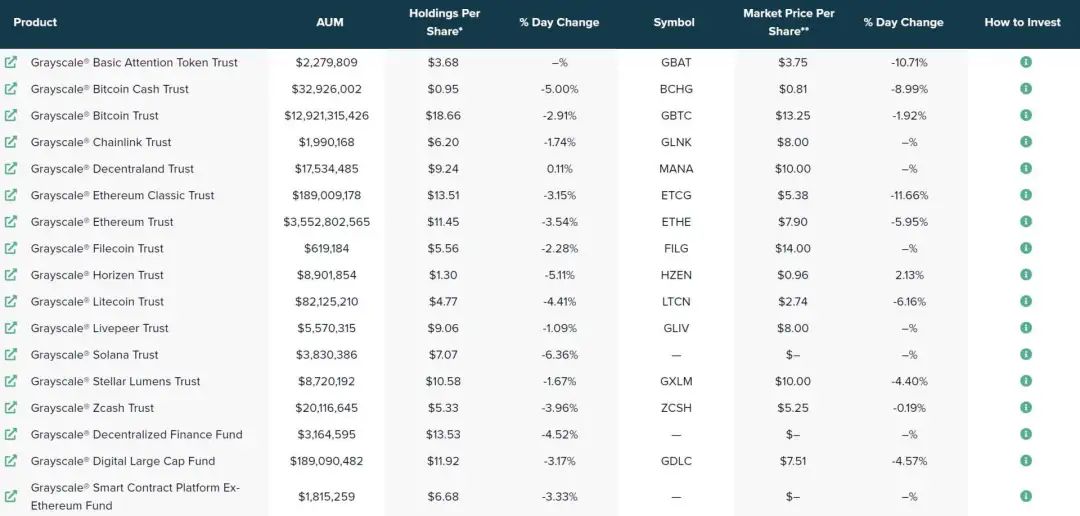
熊市里的大机构压力倍增,灰度、Tether、微策略等巨鲸会不会成为'巨雷'?

golang操作redis:写入、读取kv数据
随机推荐
File links cannot be opened or downloaded in Google browser
The list of "I'm crazy about open source" was released in the first week, with 160 developers on the list
【类和对象】深入浅出类和对象
DNS forward query:
MySQL transaction rollback, error points record
A letter to graduating college students
These two mosquito repellent ingredients are harmful to babies. Families with babies should pay attention to choosing mosquito repellent products
RestHighLevelClient获取某个索引的mapping
Reading notes of "learn to ask questions"
opencv
Tool class static method calls @autowired injected service
卡特兰数(Catalan)的应用场景
La loi des 10 000 heures ne fait pas de vous un maître de programmation, mais au moins un bon point de départ
dataworks自定义函数开发环境搭建
[open source project recommendation colugomum] this group of undergraduates open source retail industry solutions based on the domestic deep learning framework paddlepadddle
Code management tools
vmware虚拟机C盘扩容
2022年华东师范大学计科考研复试机试题-详细题解
mysql误删root账户导致无法登录
Stream stream