当前位置:网站首页>卡特兰数(Catalan)的应用场景
卡特兰数(Catalan)的应用场景
2022-07-03 06:33:00 【今天也要写bug、】
卡特兰数
卡特兰数的推导:
卡特兰数(Catalan)

应用场景
假设有n个左括号和n个右括号,他们有多少种合法的组合。
一共有C(2n,n)种组合,假设这些组合为A集合。
对于不合法的组合,一定有一个前缀,其右括号数量比左括号数量多1个,比如())(()中前缀()),而后缀一定是右括号比左括号少1一个((),我们将后缀反转(左括号变右括号,右括号变左括号),这样就变成了整个组合中右括号为n+1,左括号为n-1。反转后一共有C(2n,n-1)种组合,假设他们为B集合。
A中不合法的组合可以通过反转推出B集合中所有的情况,而B集合也可以通过反转推出A中不合法的组合。因此A中不合法的数量就等于C(2n,n-1)。
综上,合法的组合一共有C(2n,n)-C(2n,n-1)种。n个数有多少种合法的进出栈方式。
任何一个前缀出栈数量一定是少于进栈数量,因此这个问题就转化成了上面的括号问题。其组合方式也是C(2n,n)-C(2n,n-1)种。一共有n个节点,有多少种组成二叉树的方式。
有0个节点,方式为空树,组成二叉树的方式1种。
有1个节点,树为它自己,1种。
有2个节点,根+左或者根+右,2种。
有n个节点,选一个节点为头节点;头节点左边0个节点,右边n-1个节点;头结点左边1个节点,右边n-2个节点;头结点左边2个节点,右边n-3个节点。。。 可以推出k(n)=k(0)*k(n-1)+k(1)*k(n-2)+....+k(n-2)*k(1)+k(n-1)*k(0),也就是卡特兰数C(2n,n)-C(2n,n-1)种组合方式。
边栏推荐
- Simple understanding of ThreadLocal
- Redis cluster creation, capacity expansion and capacity reduction
- Install VM tools
- Creating postgre enterprise database by ArcGIS
- MATLAB如何修改默认设置
- How to scan when Canon c3120l is a network shared printer
- How matlab modifies default settings
- opencv
- 技术管理进阶——你了解成长的全貌吗?
- 数值法求解最优控制问题(一)——梯度法
猜你喜欢
轻松上手Fluentd,结合 Rainbond 插件市场,日志收集更快捷

ThreadLocal的简单理解
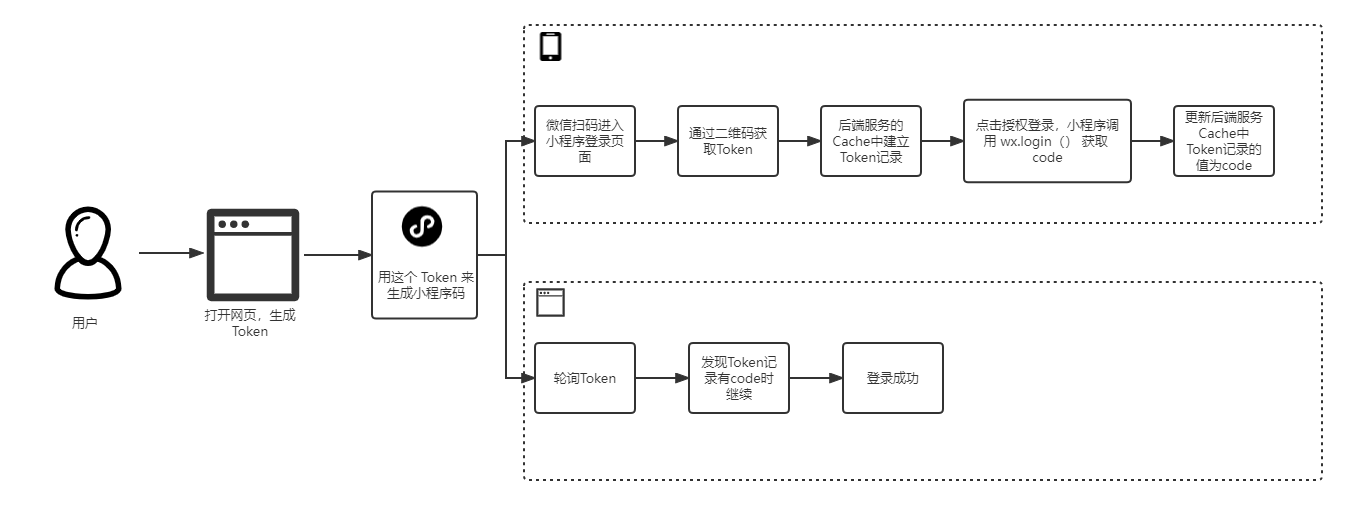
Use abp Zero builds a third-party login module (I): Principles

Fluentd facile à utiliser avec le marché des plug - ins rainbond pour une collecte de journaux plus rapide
Create your own deep learning environment with CONDA

ROS+Pytorch的联合使用示例(语义分割)

Migrate data from Mysql to tidb from a small amount of data
Summary of UI module design and practical application of agent mode

【开源项目推荐-ColugoMum】这群本科生基于国产深度学习框架PaddlePadddle开源了零售行业解决方案
Creating postgre enterprise database by ArcGIS
随机推荐
About the difference between count (1), count (*), and count (column name)
[leetcode] day93 - intersection of two arrays II
Openresty best practices
Svn branch management
[untitled] 5 self use history
ruoyi接口权限校验
2022 CISP-PTE(三)命令执行
Nacos service installation
. Net program configuration file operation (INI, CFG, config)
Request weather interface format, automation
[untitled] 8 simplified address book
Scripy learning
Merge and migrate data from small data volume, sub database and sub table Mysql to tidb
Use abp Zero builds a third-party login module (I): Principles
Unit test framework + Test Suite
Fluentd facile à utiliser avec le marché des plug - ins rainbond pour une collecte de journaux plus rapide
[open source project recommendation colugomum] this group of undergraduates open source retail industry solutions based on the domestic deep learning framework paddlepadddle
(翻译)异步编程:Async/Await在ASP.NET中的介绍
Heap sort and priority queue
opencv