当前位置:网站首页>[public key cryptography] ECC elliptic cryptosystem (implementing ElGamal encryption method)
[public key cryptography] ECC elliptic cryptosystem (implementing ElGamal encryption method)
2022-07-03 08:23:00 【Herk can't write code】
CryptoAlgor Project address ( Four experiments complete source code )
1. Github Project address
2. Gitee Project address
The directory of the project :
1. Four classical passwords /classcipher
2.DES Group password /descipher
3.RSA Public key password /rsacipher
4.ECC Public key system (Elgamal encryption ) /ellipticc
thus , Four encryption experiments are completed , in Python Realization .
All four kinds of encryption have been encapsulated into Pyhon modular , Just call it directly .
Catalog
CryptoAlgor Project address ( Four experiments complete source code )
1. About ECC Dependent Algorithm
3. be based on ECC Realization Elgamal Encryption method
1. About ECC Dependent Algorithm
1. Judge whether there is square residue , And solve the root of the square residue
2. Fractional module p Positive integer congruence of
# This document is called __util.py
from fractions import Fraction
def gcd(x, y):
""" Euclidean algorithm """
while x > 0:
x, y = y % x, x
return y
def extendGcd(a, b):
""" Extended Euclidean algorithm Congruence
seek a*x +b*y = gcd(a,b) Explain
"""
if b == 0:
return a, b
else:
x, y = extendGcd(b, a % b)
x, y = y, x - (a//b) * y
return x, y
def isQuadricReside(a, p):
""" Judge a Is it prime number p Of ` Square surplus `
---------------------------
* return 0 : a By p to be divisible by
* return 1 : a Is the mould p The square residue of
* return-1 : a Not die p The square residue of
"""
legendre = (a**int((p - 1) / 2)) % p
if legendre > 1: legendre -= p
return legendre
def calcResideRoot(a, p):
""" modulus p The square residue of a The two square roots of
---------------------------
That's the equation x^2 = a mod p Solution
* retrun : Tuple solution (x1, x2)
"""
for i in range(1, p):
if (i**2) % p == a:
return (i, p - i)
def calcCongruence(n, p):
""" Calculation a mod p Congruence positive integer of
----------------------
* n : fraction 、 Negative number, etc
* p : prime number
* retrun : Positive integer of congruence
"""
if isinstance(n, int):
# if a Integers , Then we can directly get the positive integer congruence
return n % p
# if n For the score b/a, Then calculate the positive integer congruence
# I.e. indeterminate a*x + p*y = b Solution x
a, b = n.denominator, n.numerator
coef = b // gcd(a, p)
x, _ = extendGcd(a, p)
return (coef * x) % p
2. ECC Elliptic curve class
1. establish ECC class , Implementation generation Exchange group Ep(a,b),
2. And realize the basic arithmetic operation of the Group .
# This document is called : ecc.py
from fractions import Fraction
from __util import *
class ECC():
""" Elliptic curve cryptography
Realize the operation of elliptic curve points , Encryption of messages
It can be applied to Elgamal encryption
------------------------------
this ECC class Use operator overloading , The code is more complex
See the simplified version :`ecc2.py` Medium ECC class
Curve equation : y^2 = x^3 + ax - b
* a : Ep(a, b) Medium a
* b : Ep(a, b) Medium b
* p : GF(p), y^2 mod p Medium p
"""
def __init__(self, a, b, p):
if 4 * a**3 + 27 * b**2 == 0:
print(" Illegal elliptic curve , Please re-enter ")
self.__class__.a = a # __class__ Indicates that it is set as a class member property
self.__class__.b = b # So that the inner class point visit
self.__class__.p = p
def genEset(self):
""" Generate the coordinate point set of elliptic curve Ep(a, b)
* return : Coordinate point set [(x1,y1), (x2,y2), ··· ]
"""
a, b, p = self.a, self.b, self.p
Eset = [EO.point] # Define a ` Point set Ep(a,b)` The additive unit of
for x in range(0, p):
sqr = (x**3 + a*x + b) % p # Calculate the value of the square to be drawn
if isQuadricReside(sqr, p) == 1:
# if sqr yes p The square residue of , Then ask sqr The root of the
solution = calcResideRoot(sqr, p)
Eset.append((x, solution[0]))
Eset.append((x, solution[1]))
return Eset
class point():
""" Ep(a,b) in ` Coordinates (x, y)` Instantiate as `point object `
--------------------------------------
Instantiated point Objects can be + - * Such as operation
"""
def __init__(self, *point):
""" Get instance object ECC() Medium a, p, ` Coordinates point`
* a, p : Ep(a, b) Medium a, p
* point : Coordinate point on elliptic curve (x, y)
"""
# Inherit external class member properties ECC.a, ECC.p
self.a, self.p, self.point = ECC.a, ECC.p, point
def __add__(self, other):
""" Overload operator `+`: Define the addition of points on an ellipse
* self : point object P:(x1, y1)
* other : point object Q:(x2, y2)
* retrun: point object P+Q:(x3,y3)
"""
a, p, P, Q = self.a, self.p, self, other
(x1, y1), (x2, y2) = self.point, other.point
if P.point == EO.point: return Q # EO+Q=Q
if Q.point == EO.point: return P # P+EO=P
if x1==x2 and y1!=y2: return EO # P+Q=EO
if x1!=x2: lamb = Fraction(y2-y1, x2-x1)
if x1==x2: lamb = Fraction(3*x1*x1+a, 2*y1)
lamb = calcCongruence(lamb, p)
x3 = lamb**2 - x1 - x2
x3 = calcCongruence(x3, p)
y3 = lamb * (x1 - x3) - y1
y3 = calcCongruence(y3, p)
return ECC.point(x3, y3)
def __mul__(self, coef):
""" Overload operator `*`: Multiply the number of points on the ellipse for example Point*3 """
sums = self
for _ in range(1, coef): sums += self
return sums
def __rmul__(self, other):
""" Overload operator `*`: Multiply the number of points on the ellipse for example 3*Point """
return self * other
def __neg__(self):
""" Overload operator `-`: The additive inverse of a point on an ellipse """
x, y = (self.point[0], ECC.p-self.point[1])
y = 0 if y == ECC.p else y
return ECC.point(x, y)
def __sub__(self, other):
""" Overload operator `-`: Subtraction of points on ellipse """
other = - other # Returns the inverse of addition be P-Q = P+(-Q)
return self + other
def __repr__(self):
""" overloaded function `print`: Print object point The point of (x,y) """
# obtain point Coordinate point of the object point (0,0) Print letter O
disp = self.point
disp = 'O' if disp==EO.point else disp
return str(disp)
# Global variables : Custom addition unit , namely EO.point = (0, 0)
# ECC() The middle number is arbitrary , point(x,0) in x casual , y Must be 0 or p
EO = ECC(1,1,1).point('O', 'O')
""" Why take a single yuan ('O', 'O') ?
because ('O', 'O') Not even coordinates , Nature is not in the curve y^3=x^3+ax+b On
It's just a symbol , It's written in ('O', 'O') Just because of the coordinates (x,y) There are two components
Just for the convenience of calculation , It's just a symbol
"""
if __name__ == '__main__':
ellip = ECC(1, 1, 23) # Instantiate a Ep(a,b) object
P = ellip.point(3, 10) # Instantiation Ep(a,b) Upper point object
Q = ellip.point(9, 7) # Instantiation Ep(a,b) Upper point object
print("P+Q:", P + P)3. be based on ECC Realization Elgamal Encryption method
1. With 《 Modern cryptography Yang Bo 》 Example 4-36, verification Elgaml The encryption process ,
2. And based on Ciphertext 、 Plaintext Crack Alice The private key .
# This code is based on ECC class Realization Elgamal encryption
from ellipticc import ECC
import time
def takeTime(func):
""" Decorator : Calculating the running time of the function """
def decorated(*args):
startime = time.time()
func(*args)
endtime = time.time()
taketime = round((endtime - startime)*10**3)
print(f"-> The computation is time-consuming : {taketime} millisecond ")
return func
return decorated
@takeTime
def Elgamal_exam436():
# utilize ECC Elliptic cryptography , Realization Elgamma encryption
# Open elliptic curve ECC Parameters of Ep(a,b)、G
# Alice Select an integer private key Nk4
# Alice Publish your public key PA=NA*G
ellip = ECC(-1, 188, 751)
G = ellip.point(0, 376)
PA = ellip.point(201, 5)
# Bob Choose random numbers k, For messages PM Encrypt to get ciphertext
# Bob Send ciphertext C = [(676, 558), (385, 328)]
k = 386
PM = ellip.point(562, 201)
C = [k*G, PM + k*PA]
print("\n The secret is :", C)
@takeTime
def crackElgamal():
""" Solve the example Alice The private key """
ellip = ECC(-1, 188, 751)
PM = ellip.point(562, 201)
C1 = ellip.point(676, 558)
C2 = ellip.point(385, 328)
for i in range(1, 1000):
tmp = C2 - i*C1
if tmp.point == PM.point:
print("\nAlice The selected key is :", i)
return i
print("\n Not cracked successfully , Please increase the number of iterations ")
return 0
if __name__ == '__main__':
Elgamal_exam436()
crackElgamal()边栏推荐
- 数据的存储
- [K & R] Chinese Second Edition personal questions Chapter1
- Basic operation and process control 2
- go 解析身份证
- [global product discovery 2] the first pure cloud augmented reality (AR) platform - Israel
- P1896 [scoi2005] non aggression (shape pressure DP)
- Base64 and base64url
- P2704 [noi2001] artillery position (shape pressure DP)
- Dotween plug-in
- Golang 中string和int类型相互转换
猜你喜欢

MAE

Some understandings of 3dfiles
the installer has encountered an unexpected error installing this package
animation

數據庫應用技術課程設計之商城管理系統

Unity2019_ Lighting system

Chocolate installation

Redis data structure
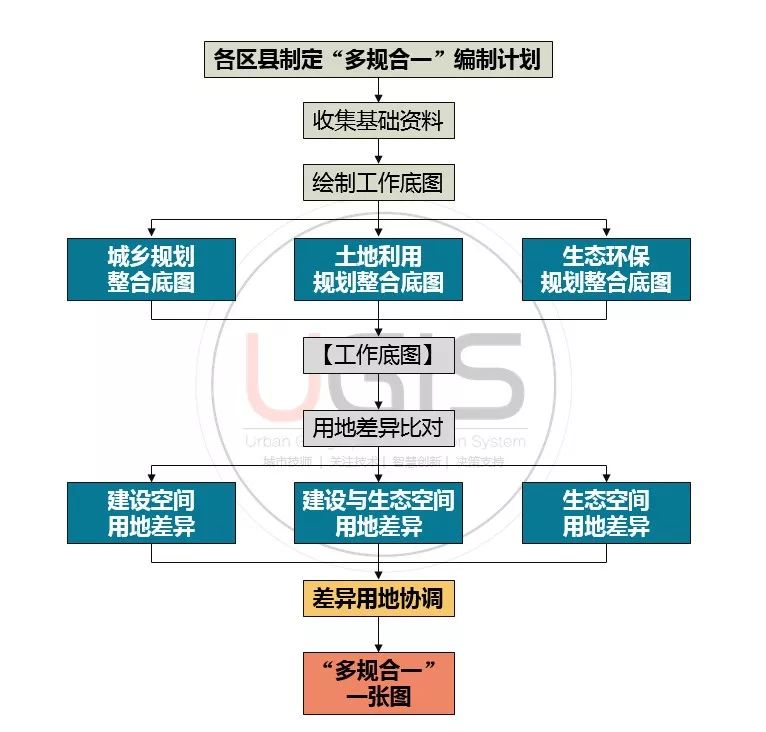
100 GIS practical application cases (78) - Multi compliance database design and data warehousing

Scite change background color
随机推荐
[set theory] order relation (hastu example | divisive relation hastu | inclusive relation hastu | refinement relation hastu)
Youyou1 of xlua knapsack system
Sequence of map implementation classes
Kunlunbase meetup is waiting for you!
A tunnel to all ports of the server
unity2019_ Input management
Base64 and base64url
[updating] wechat applet learning notes_ three
Conversion between string and int types in golang
Why can void * be a general pointer
使用base64编码传图片
【云原生】微服务之Feign的介绍与使用
Dealing with duplicate data in Excel with xlwings
MySQL containerization (1) docker installation MySQL
UE4 plug in development
Minimap plug-in
What does (+) in Oracle mean
2021-10-19
Huawei interview summary during the epidemic
Base64编码简介