当前位置:网站首页>Binary search tree (features)
Binary search tree (features)
2022-07-07 16:36:00 【Joey Liao】
List of articles
First ,BST Everyone should be familiar with the characteristics of :
- about BST Each node of
node, The values of the left subtree nodes are higher thannodeIt's worth less , The values of the right subtree nodes are greater thannodeIt's worth a lot . - about BST Each node of node, Its left subtree and right subtree are BST.
Binary search trees are not complicated , But I think it can be regarded as half of the data structure field , Based on the direct BST The data structure of is AVL Trees , Red and black trees and so on , Has the property of self-equilibrium , Can provide logN Level addition, deletion, query and modification efficiency ; also B+ Trees , Structures such as line segment trees are based on BST The idea to design .
From the perspective of doing algorithm problems BST, Except for its definition , Another important property :BST The middle order traversal result of is ordered ( Ascending ).
in other words , If you enter a tree BST, The following code can BST The values of each node in the are printed in ascending order :
void traverse(TreeNode root) {
if (root == null) return;
traverse(root.left);
// Middle order traversal code position
print(root.val);
traverse(root.right);
}
Search for the first K Small elements
Force to buckle 230 topic 「 Binary search tree K Small elements 」
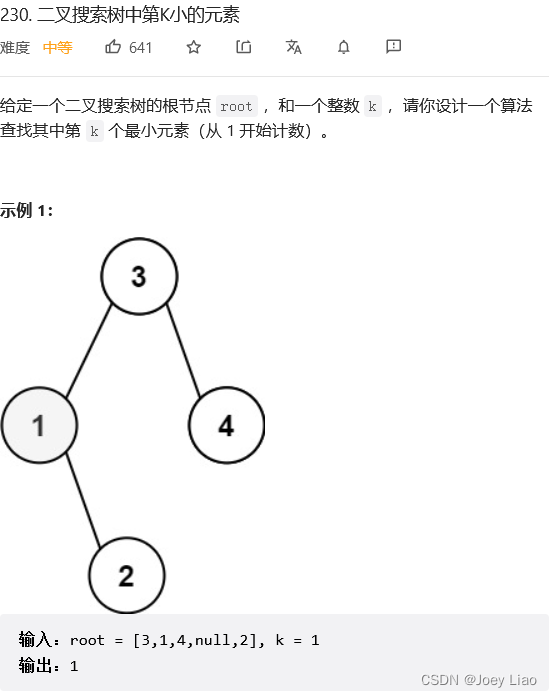
, A direct idea is to sort in ascending order , Then find the second k Two elements .BST The middle order traversal of is actually the result of ascending sorting , Find the first k An element is certainly not difficult .
int kthSmallest(TreeNode root, int k) {
// utilize BST Middle order ergodic property of
traverse(root, k);
return res;
}
// Records of the results
int res = 0;
// Record the ranking of the current element
int rank = 0;
void traverse(TreeNode root, int k) {
if (root == null) {
return;
}
traverse(root.left, k);
/* Middle order traversal code position */
rank++;
if (k == rank) {
// Find No k Small elements
res = root.val;
return;
}
/*****************/
traverse(root.right, k);
}
If we follow the method we just mentioned , utilize 「BST Medium order traversal is the result of ascending sorting 」 This nature , Every time you look for k Small elements should be traversed once in the middle order , The worst time complexity is O(N),N yes BST Number of nodes .
Need to know BST The nature is very awesome , Improved self balance like red black tree BST, Add, delete, check and change are O(logN) Complexity , Let you count a number k Minor elements , The time complexity should be O(N), A little inefficient .
So back to the question , Want to find the second k Small elements , Or find a ranking of k The elements of , If you want to achieve logarithmic complexity , The key is that each node has to know its own ranking .
For example, you asked me to find a ranking of k The elements of , The current node knows that it ranks No m, Then I can compare m and k Size :
If m == k, Obviously, I found the second k Elements , Just return to the current node .
If k < m, That means ranking No k The element of is in the left subtree , So you can search the left subtree k Elements .
If k > m, That means ranking No k The element of is in the right subtree , So you can go to the right subtree to search for the second k - m - 1 Elements .
In this way, the time complexity can be reduced to O(logN) 了 .
that , How to let each node know its ranking ?
That's what we said before , Additional information needs to be maintained in the binary tree node . Each node needs to record , How many nodes does the binary tree with its own root have .
in other words , We TreeNode The fields in should be as follows :
class TreeNode {
int val;
// The total number of nodes in the tree with this node as the root
int size;
TreeNode left;
TreeNode right;
}
With size Field , Plus BST The property that nodes are small on the left and large on the right , For each node node You can go through node.left Deduce node Ranking , So as to achieve the logarithmic algorithm we just mentioned .
Of course ,size Fields need to be properly maintained when adding or deleting elements , The force buckle provides TreeNode It's not size Of this field , So we can only use this problem BST The feature of middle order traversal realizes , But the optimization idea we mentioned above is BST Common operations for , It is still necessary to understand .
BST Transform cumulative tree
Force to buckle 538 Title and 1038 The questions are all this question Convert binary search tree to accumulation tree
In fact, it is the middle order traversal of binary tree , use sum To record the current cumulative sum
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
int sum=0;
public TreeNode convertBST(TreeNode root) {
traverse(root);
return root;
}
public void traverse(TreeNode root){
if(root==null){
return ;
}
traverse(root.right);
sum+=root.val;
root.val=sum;
traverse(root.left);
}
}
边栏推荐
- 两类更新丢失及解决办法
- How to implement backspace in shell
- thinkphp3.2.3中设置路由,优化url
- 47_ Contour lookup in opencv cv:: findcontours()
- Bidding announcement: Fujian Rural Credit Union database audit system procurement project (re bidding)
- Unity3d click events added to 3D objects in the scene
- 【Android -- 数据存储】使用 SQLite 存储数据
- PHP has its own filtering and escape functions
- URL和URI的关系
- Communication mode between application program and MATLAB
猜你喜欢

AutoLISP series (3): function function 3

【Android -- 数据存储】使用 SQLite 存储数据

Lecturer solicitation order | Apache seatunnel (cultivating) meetup sharing guests are in hot Recruitment!
Notification uses full resolution
What are compiled languages and interpreted languages?

1亿单身男女“在线相亲”,撑起130亿IPO
Logback logging framework third-party jar package is available for free

AutoLISP series (2): function function 2
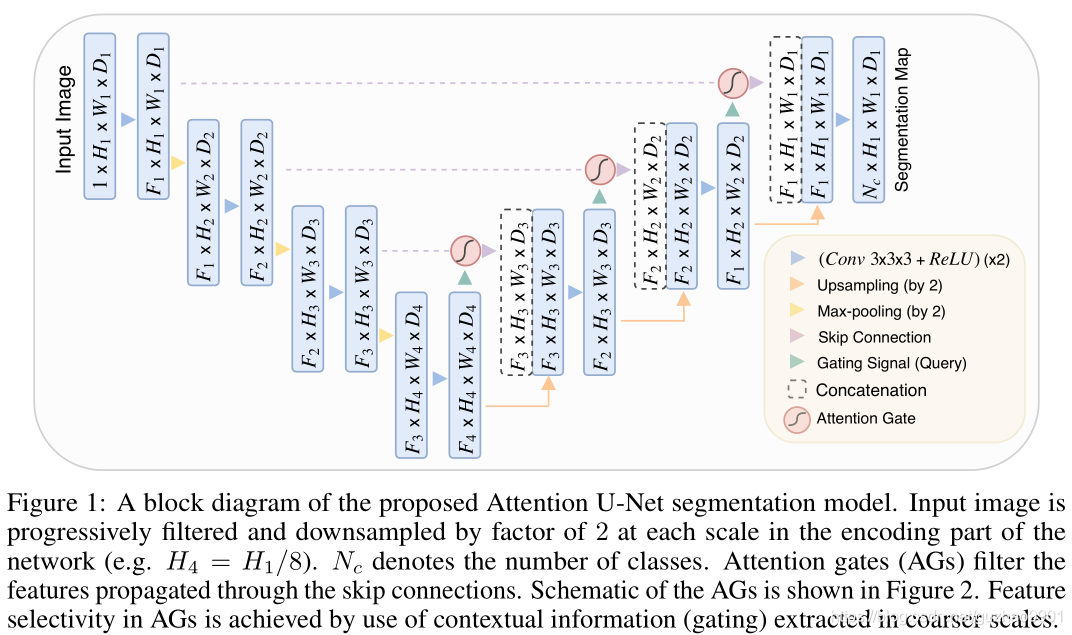
【医学分割】attention-unet
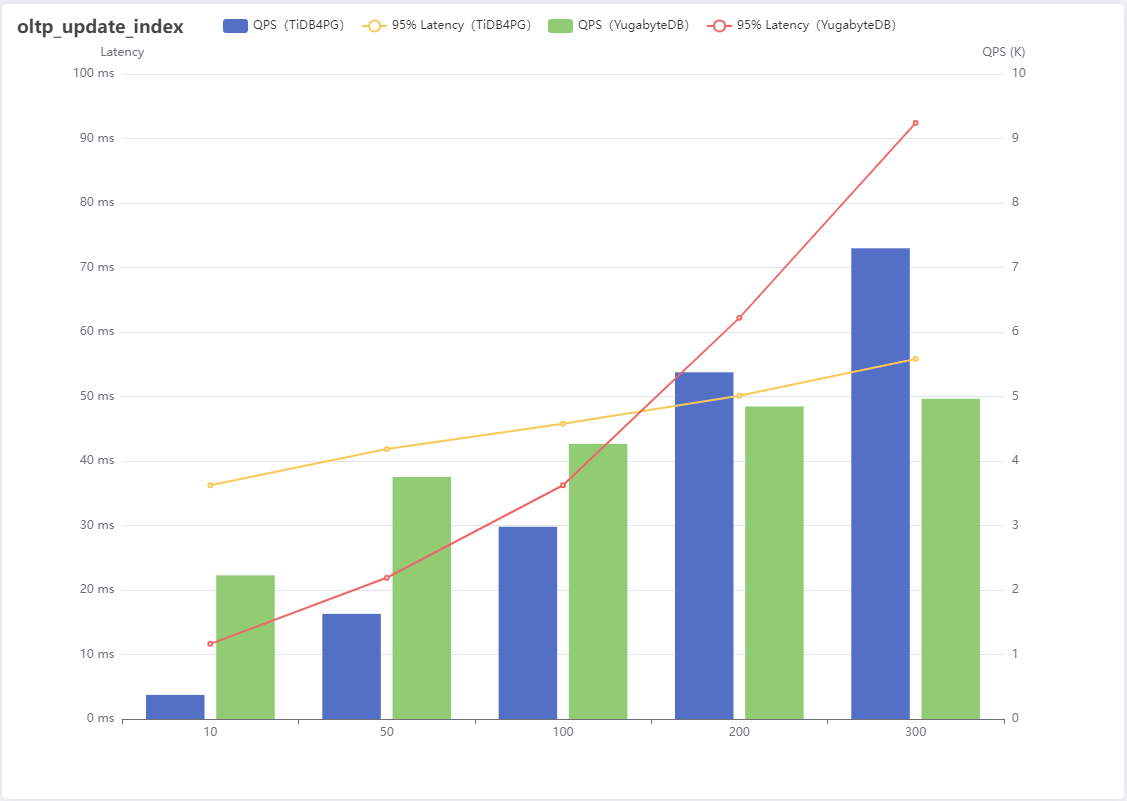
TiDB For PostgreSQL和YugabyteDB在Sysbench上的性能对比
随机推荐
Xcode Revoke certificate
47_ Contour lookup in opencv cv:: findcontours()
Enterprise log analysis system elk
平衡二叉树(AVL)
Balanced binary tree (AVL)
Laravel changed the session from file saving to database saving
记录Servlet学习时的一次乱码
95.(cesium篇)cesium动态单体化-3D建筑物(楼栋)
01tire+ chain forward star +dfs+ greedy exercise one
47_Opencv中的轮廓查找 cv::findContours()
js中复选框checkbox如何判定为被选中
Notification uses full resolution
2022 the 4th China (Jinan) International Smart elderly care industry exhibition, Shandong old age Expo
【C 语言】 题集 of Ⅹ
markdown公式编辑教程
Find tags in prefab in unity editing mode
无法将“pip”项识别为 cmdlet、函数、脚本文件或可运行程序的名称
torch.numel作用
Three. JS series (2): API structure diagram-2
three.js打造酷炫下雪效果