当前位置:网站首页>过拟合与正则化
过拟合与正则化
2022-07-05 05:27:00 【李峻枫】
过拟合
这是一个神经网络训练过程中,经常会遇到的问题,简单来说,就是模型的表现了,学习能力太强了,以至于把训练集的所有细节都记录下来了。当遇到测试集,就是之前完全没有见过的数据的时候,就会出现明显的错误。
产生原因
最本质的一个原因就是:参数过多(模型过于复杂)
其他原因就是:
- 测试集与训练集的分布不一样
- 训练集的数量太少
解决办法
针对上述原因,可以提出几种对策
- 降低模型复杂度,常用的有正则化。
- 增强训练集
范数Norm(Minkowski距离)
定义
范数是一个函数,其赋予某个向量空间中的每个向量一长度或大小。
对于零向量,其长度为0。
∥ x ∥ p = ( ∑ i = 1 n ∣ x ∣ p ) 1 p \lVert x \rVert_p = \left(\displaystyle\sum_{i=1}^n \lvert x\rvert^p\right)^{\frac{1}{p}} ∥x∥p=(i=1∑n∣x∣p)p1
范数的性质
- 非负性 ∥ x ∥ ≥ 0 \lVert x\rVert \ge 0 ∥x∥≥0
- 齐次性 ∥ c x ∥ = ∣ c ∣ ∥ x ∥ \lVert cx\rVert=\lvert c\rvert \lVert x\rVert ∥cx∥=∣c∣∥x∥
- 三角不等式 ∥ x + y ∥ ≤ ∥ x ∥ + ∥ y ∥ \lVert x + y\rVert \leq \lVert x\rVert +\Vert y\rVert ∥x+y∥≤∥x∥+∥y∥
范数特征
- L 0 L_0 L0范数:非零元素个数
- L 1 L_1 L1范数:绝对值之和
- L 2 L_2 L2范数:欧拉距离
- L ∞ L_{\infin} L∞范数:绝对值最大的元素的绝对值
正则化
目标函数加上一个范数,作为惩罚项。如果一个参数越大,它就会使范数增大,即惩罚项增大。因此在范数的作用下,不少参数都在不断变小。
参数越小,说明其在神经网络中发挥的作用越小,即对最终结果的影响越小,因此可以使得模型更加简单,而且更加具有泛化能力。
正则化也是一种优胜劣汰的思想,虽然很多参数对模型都有用,但最终只有重要的参数才能被保留下来(值较大,对结果影响大),而大部分参数都被淘汰了(值很小,对结果影响不大)。
边栏推荐
- sync. Interpretation of mutex source code
- 剑指 Offer 35.复杂链表的复制
- Software test -- 0 sequence
- Pointnet++ learning
- Reverse one-way linked list of interview questions
- [to be continued] [depth first search] 547 Number of provinces
- kubeadm系列-00-overview
- 动漫评分数据分析与可视化 与 IT行业招聘数据分析与可视化
- 26、 File system API (device sharing between applications; directory and file API)
- 每日一题-搜索二维矩阵ps二维数组的查找
猜你喜欢
随机推荐
[sum of two numbers] 169 sum of two numbers II - enter an ordered array
[转]:Apache Felix Framework配置属性
Find a good teaching video for Solon framework test (Solon, lightweight application development framework)
lxml. etree. XMLSyntaxError: Opening and ending tag mismatch: meta line 6 and head, line 8, column 8
Romance of programmers on Valentine's Day
Reader writer model
Es module and commonjs learning notes -- ESM and CJS used in nodejs
[allocation problem] 135 Distribute candy
Animation scoring data analysis and visualization and it industry recruitment data analysis and visualization
[to be continued] [UE4 notes] L2 interface introduction
The next key of win generates the timestamp file of the current day
[allocation problem] 455 Distribute cookies
High precision subtraction
[转]MySQL操作实战(一):关键字 & 函数
Pointnet++的改进
服务熔断 Hystrix
Chapter 6 data flow modeling - after class exercises
[转]: OSGI规范 深入浅出
Shell Sort
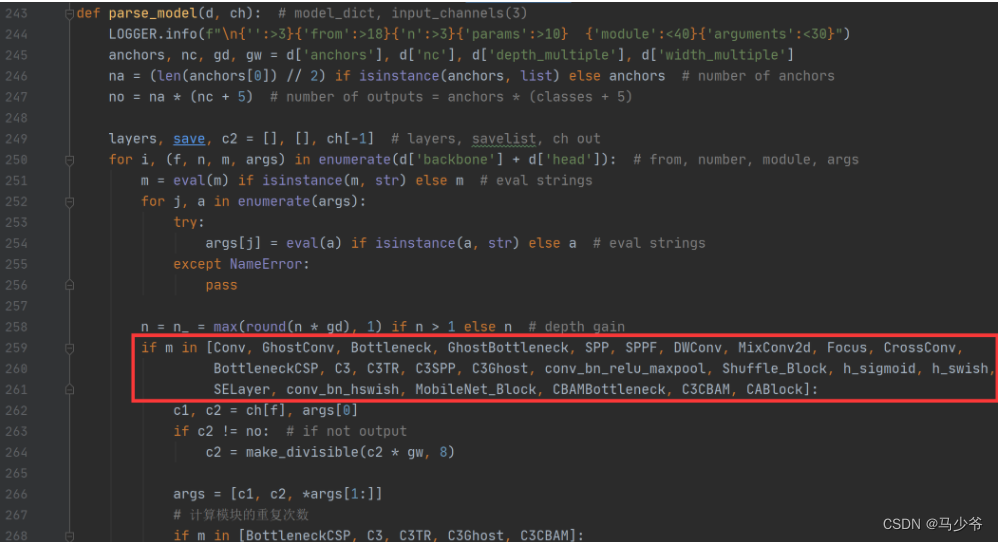
Yolov5 adds attention mechanism
![[转]MySQL操作实战(三):表联结](/img/70/20bf9b379ce58761bae9955982a158.png)