当前位置:网站首页>2019 Nanchang (relive the classic)
2019 Nanchang (relive the classic)
2022-07-02 21:41:00 【C_ eeking】
2019 nanchang ( Revisit the classic )
Introduction
It's very difficult. , Once again aware of the gap in knowledge points
Knowledge points involved
Pressure DP, thinking , Combinatorial mathematics ,DSU on Tree, Line segment tree
link :2019 Nanchang Regional
subject
C
The main idea of the topic : Give a large nonnegative integer n n n, Calculate integer pairs that meet the following conditions ( i , j ) (i,j) (i,j) The number of , n n n Given in binary
- 0 ≤ j ≤ i ≤ n 0\le j\le i\le n 0≤j≤i≤n
- i & n = i i \&n=i i&n=i
- i & j = 0 i\& j=0 i&j=0
Ideas : Set the conditions according to the questions , Constructed i i i Only in n n n Of 1 There is a value corresponding to the bit , and j j j No more than i i i Under the premise of , The value of each bit is arbitrary , In order to ensure i i i Greater than j j j, In the structure i i i When , From low to high structures , hypothesis i The current bit of is fixed to 1, Other high positions are fixed as 0, Classify and discuss the low order situation , It's like 000001xxxxx The situation of , Suppose it is the penultimate p p p position , n n n This bit corresponds to 1, Reciprocal 1 − p 1-p 1−p All in all k k k individual 1, m m m individual 0, Then the total number of schemes can be obtained as :
C k 0 2 m + k + C k 1 2 m + k − 1 + ⋯ + C k k 2 m C_k^02^{m+k}+C_k^12^{m+k-1}+\dots+C_k^k2^m Ck02m+k+Ck12m+k−1+⋯+Ckk2m
= 2 m ( C k 0 2 k + C k 1 2 k − 1 + ⋯ + C k k ) =2^m(C_k^02^k+C_k^12^{k-1}+\dots+C_k^k) =2m(Ck02k+Ck12k−1+⋯+Ckk)
= 2 m ( C k k 2 k + C k k − 1 2 k − 1 + ⋯ + C k 0 2 0 ) =2^m(C_k^k2^k+C_k^{k-1}2^{k-1}+\dots+C_k^02^0) =2m(Ckk2k+Ckk−12k−1+⋯+Ck020)
So we can deduce the formula , But obviously the formula is more complicated , It can be further simplified
It is known that ( 1 + x ) n = C n 0 x 0 + C n 1 x 1 + … C n n x n (1+x)^n=C_n^0x^0+C_n^1x^1+\dots C_n^nx^n (1+x)n=Cn0x0+Cn1x1+…Cnnxn
take x = 2 x=2 x=2 Brought in
( 1 + 2 ) n = C n 0 2 0 + C n 1 2 1 + … C n n 2 n (1+2)^n=C_n^02^0+C_n^12^1+\dots C_n^n2^n (1+2)n=Cn020+Cn121+…Cnn2n
Therefore, the final formula can be deduced as 2 m 3 k 2^m3^k 2m3k
Code
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int maxn=1e5+5;
const int mod=1e9+7;
int T;
char s[maxn];
int qpow(int power,int base) {
int result=1;
while(power) {
if(power&1)
result=result*base%mod;
power>>=1;
base=base*base%mod;
}
return result%mod;
}
signed main() {
scanf("%lld",&T);
while(T--) {
scanf("%s",s+1);
int len=strlen(s+1),cnt=0,res=0;
for(int i=len; i>=1; i--)
if(s[i]=='1') {
res=(res+(qpow(cnt,3)*qpow(len-i-cnt,2))%mod)%mod;
cnt++;
}
res=(res+1)%mod;// add i=j=0
printf("%lld\n",res);
}
return 0;
}
E
The main idea of the topic : Give a n n n An undirected graph of nodes , Yes m m m Right edge , Each side is either black or white , Now select some edges from them to construct a new graph , Make the graph connected , And you can only choose no more than k k k White edge , Find the maximum sum of edge weights that can be obtained by the new graph , If the new graph cannot be connected , Output -1
Ideas : First select all the black edges , Then use the union search mark , Then sort the white edges from large to small , Traverse the white edge , Select the white edge on the premise of ensuring connectivity , If there are more times , Choose the white edge with large edge weight
Code
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int maxn=5e5+5;
int T,n,m,k,f[maxn];
bool vis[maxn];
int Seek(int x) {
// Path compression
if(x==f[x])return x;
return f[x]=Seek(f[x]);
}
void Union(int x,int y) {
// Merge
int fx=Seek(x),fy=Seek(y);
if(fx!=fy)f[fx]=fy;
}
struct node {
// Overload ratio size
int from,to,w;
bool operator<(const node &a)const {
return w>a.w;
}
} e[maxn];
signed main() {
scanf("%lld",&T);
while(T--) {
scanf("%lld%lld%lld",&n,&m,&k);
memset(vis,0,sizeof(vis));// initialization
int sum=0,cnt=0;
bool flag=0;
for(int i=1; i<=n; i++)f[i]=i;
while(m--) {
int u,v,w,c;
scanf("%lld%lld%lld%lld",&u,&v,&w,&c);
if(c) {
// White edges need to be entered
e[++cnt].from=u;
e[cnt].to=v;
e[cnt].w=w;
} else {
// The black edge is directly used
if(Seek(u)!=Seek(v))
Union(u,v);
sum+=w;
}
}
sort(e+1,e+1+cnt);// Sort
for(int i=1; i<=cnt&&k; i++) {
// Traverse all white edges , First, ensure connectivity
int u=e[i].from,v=e[i].to;
if(Seek(u)!=Seek(v)) {
Union(u,v);
k--;
sum+=e[i].w;
vis[i]=1;
}
}
for(int i=1; i<=n; i++)
if(Seek(i)!=Seek(1)) {
flag=1;
break;
}
if(flag) {
printf("-1\n");
continue;
}
for(int i=1; i<=cnt&&k; i++)
if(vis[i])continue;
else {
k--;
sum+=e[i].w;
}
printf("%lld\n",sum);
}
return 0;
}
G
The main idea of the topic : A little
Ideas : First , The module given by the topic is a composite number , The maximum prime factor is 2803, that , Greater than 2803 The factorial corresponding to the value of is bound to result in 0, Just think about it 1 ~ 2803 The number in this range is enough , Then just violence O ( n 2 ) O(n^2) O(n2) Traverse all the intervals , Judge the maximum value that can be reached by different interval sizes , Finally, find the corresponding answer according to the input ( Be careful , The larger the range , The value obtained must be larger )
Code
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int maxn=1e5+5;
const int mod=998857459;
int n,m,a[maxn],mul[maxn]= {
1},cnt,sum[3000],ans[maxn];
struct node {
int val,id;
} res[3000];
signed main() {
scanf("%lld%lld",&n,&m);
for(int i=1; i<2803; i++)// Preprocessing factorials
mul[i]=(mul[i-1]*i)%mod;
for(int i=1; i<=n; i++) {
int x;
scanf("%lld",&x);
a[i]=mul[x];// Records of the results
}
for(int i=1; i<=n; i++)
if(a[i]) {
// Re record the results
res[++cnt].val=a[i];
res[cnt].id=i;
sum[cnt]=sum[cnt-1]+res[cnt].val%mod;// The prefix and
}
for(int i=1; i<=cnt; i++)
for(int j=i; j<=cnt; j++)// Try different ranges
ans[res[j].id-res[i].id+1]=max(ans[res[j].id-res[i].id+1],(sum[j]-sum[i-1]+mod)%mod);
while(m--) {
int x,len=INF;
scanf("%lld",&x);
for(int i=1; i<=n; i++)
if(ans[i]>=x) {
len=i;
break;
}
if(len==INF)printf("-1\n");
else printf("%lld\n",len);
}
return 0;
}
L
The main idea of the topic : Yes n n n A football team takes part in the match , Each team will compete with the rest n − 1 n-1 n−1 Each team has a match , Now give the results of all competitions , Judge whether there is a champion , If there is an output number, otherwise the corresponding string is output , The winner of every game gets 3 branch , Each side gets a draw 1 branch , The champion is the team with the largest score and the largest number of net goals ( Net goals = goals - Number of balls lost )
Ideas : Direct violence statistics , Finally, sort and judge according to the requirements of the topic 1
Code
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int maxn=1e3+50;
int n,match[121][121];
struct node {
int get,score,id;
bool operator<(const node& a)const {
if(score==a.score)return get>a.get;
return score>a.score;
}
} team[121];
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n;
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++)
cin >>match[i][j];
team[i].id=i;
}
if(n==1) {
cout <<1;
return 0;
}
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)// It's actually heavy here , But the relative size remains the same , No effect
if(i!=j) {
team[i].get+=match[i][j];
team[i].get-=match[j][i];
team[j].get+=match[j][i];
team[j].get-=match[i][j];
if(match[i][j]>match[j][i])team[i].score+=3;
else if(match[i][j]==match[j][i])team[i].score++,team[j].score++;
else team[j].score+=3;
}
sort(team+1,team+1+n);
if(team[1].score==team[2].score&&team[1].get==team[2].get)cout <<"play-offs";
else cout <<team[1].id;
return 0;
}
reference
边栏推荐
- Redis分布式锁故障,我忍不住想爆粗...
- Pyqt picture decodes and encodes and loads pictures
- 26 FPS video super-resolution model DAP! Output 720p Video Online
- Download vagrant box file locally from Atlas and configuring it
- Adding data to the head or tail of the rar file can still decompress normally
- Research Report on ranking analysis and investment strategic planning of RFID market competitiveness of China's industrial manufacturing 2022-2028 Edition
- Analysis of enterprise financial statements [1]
- Go web programming practice (2) -- process control statement
- China's Micro SD market trend report, technology dynamic innovation and market forecast
- [shutter] shutter layout component (Introduction to layout component | row component | column component | sizedbox component | clipoval component)
猜你喜欢
![[shutter] statefulwidget component (floatingactionbutton component | refreshindicator component)](/img/17/b5889ec263687aeacf19214785ea8a.jpg)
[shutter] statefulwidget component (floatingactionbutton component | refreshindicator component)

Common routines of compressed packets in CTF

5 environment construction spark on yarn

Research Report on ranking analysis and investment strategic planning of RFID market competitiveness of China's industrial manufacturing 2022-2028 Edition
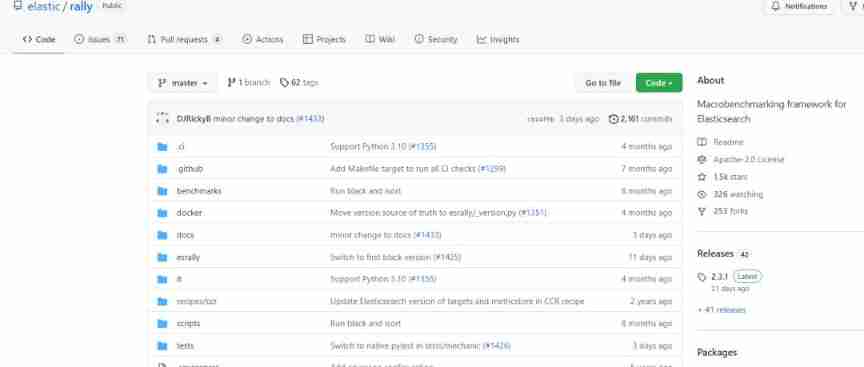
How does esrally perform simple custom performance tests?
Go language learning summary (5) -- Summary of go learning notes

Today, I met a Alipay and took out 35K. It's really sandpaper to wipe my ass. it's a show for me
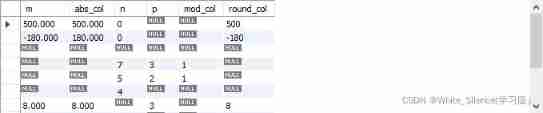
MySQL learning record (7)
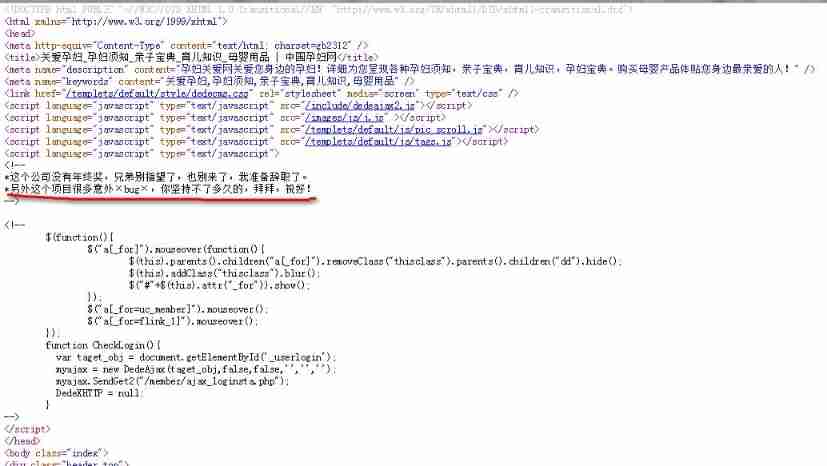
Unexpectedly, there are such sand sculpture code comments! I laughed

Read a doctor, the kind that studies cows! Dr. enrollment of livestock technology group of Leuven University, milk quality monitoring
随机推荐
Report on investment development and strategic recommendations of China's vibration isolator market, 2022-2027
Common authority query instructions in Oracle
Construction and maintenance of business websites [6]
Spend more time with your computer on this special holiday, HHH
MySQL learning record (8)
【零基础一】Navicat下载链接
AES encryption CBC mode pkcs7padding filling Base64 encoding key 32byte iv16byte
Find objects you can't see! Nankai & Wuhan University & eth proposed sinet for camouflage target detection, and the code has been open source
Research Report on plastic antioxidant industry - market status analysis and development prospect forecast
In depth research and investment feasibility report on the global and China active vibration isolation market 2022-2028
Analyze comp-206 advanced UNIX utils
It is said that this year gold three silver four has become gold one silver two..
Baidu sued a company called "Ciba screen"
Plastic floating dock Industry Research Report - market status analysis and development prospect forecast
I drew a Gu ailing with characters!
Basic IO interface technology - microcomputer Chapter 7 Notes
Codeworks global round 19 (CF 1637) a ~ e problem solution
Analysis of enterprise financial statements [3]
Research Report on ranking analysis and investment strategic planning of RFID market competitiveness of China's industrial manufacturing 2022-2028 Edition
D4: unpaired image defogging, self enhancement method based on density and depth decomposition (CVPR 2022)