【LeetCode】合并

一、合并两个有序链表

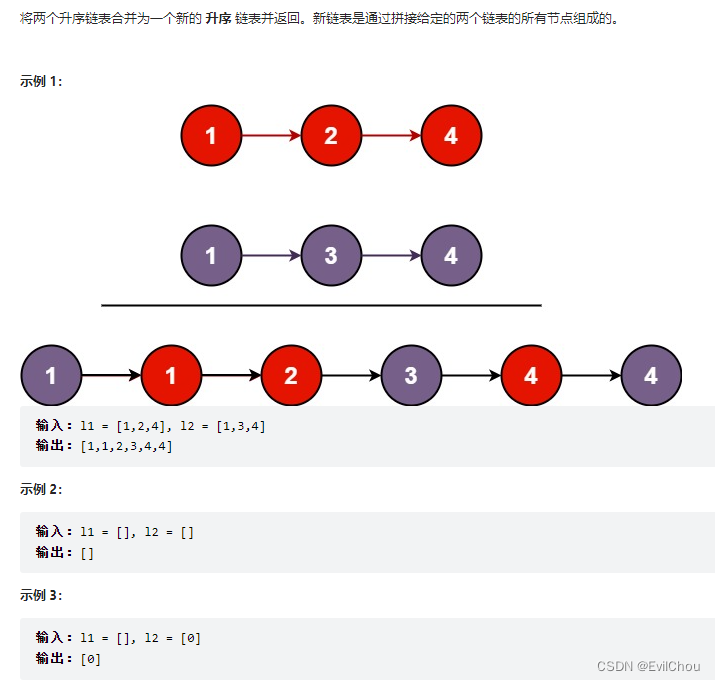
 方法一：暴力解法

当 l1 和 l2 都不是空链表时，判断 l1 和 l2 哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。

首先，我们设定一个哨兵节点 prehead ，这可以在最后让我们比较容易地返回合并后的链表。我们维护一个 prev 指针，我们需要做的是调整它的 next 指针。然后，我们重复以下过程，直到 l1 或者 l2 指向了 null ：如果 l1 当前节点的值小于等于 l2 ，我们就把 l1 当前的节点接在 prev 节点的后面同时将 l1 指针往后移一位。否则，我们对 l2 做同样的操作。不管我们将哪一个元素接在了后面，我们都需要把 prev 向后移一位。

在循环终止的时候， l1 和 l2 至多有一个是非空的。由于输入的两个链表都是有序的，所以不管哪个链表是非空的，它包含的所有元素都比前面已经合并链表中的所有元素都要大。这意味着我们只需要简单地将非空链表接在合并链表的后面，并返回合并链表即可。

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
    
        ListNode prehead = new ListNode(-1); //维护一个新的节点prehead
        ListNode prev = prehead; //prehead的指针prev

        while(list1 != null && list2 != null){
            if(list1.val <= list2.val){
                prev.next = list1;
                list1 = list1.next;
            }else{
                prev.next = list2;
                list2 = list2.next;
            }
            prev = prev.next;
        }
        prev.next = list1 == null ? list2 : list1;
        return prehead.next;
    }
}

方法二：递归
思路

我们可以如下递归地定义两个链表里的 merge 操作（忽略边界情况，比如空链表等）：

也就是说，两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。

算法

我们直接将以上递归过程建模，同时需要考虑边界情况。

如果 l1 或者 l2 一开始就是空链表 ，那么没有任何操作需要合并，所以我们只需要返回非空链表。否则，我们要判断 l1 和 l2 哪一个链表的头节点的值更小，然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空，递归结束。

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        if(list1 == null){
            return list2;
        }else if(list2 == null){
            return list1;
        }else if(list1.val < list2.val){
            list1.next = mergeTwoLists(list1.next,list2);
            return list1;
        }else{
            list2.next = mergeTwoLists(list1,list2.next);
            return list2;
        }
       
    }
}

 二、合并两个有序数组

方法一：将数组2直接放到数组1的尾部，合并后再排序（不建议这种方法）

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        for(int i = 0;i != n;i++){
            nums1[m+i] = nums2[i];
        }
        Arrays.sort(nums1);
    }
}

复杂度分析

时间复杂度：O((m+n)log(m+n))。
排序序列长度为 m+n，套用快速排序的时间复杂度即可，平均情况为 O((m+n)log(m+n))。

空间复杂度：O(log(m+n))。
排序序列长度为m+n，套用快速排序的空间复杂度即可，平均情况为 O(log(m+n))。

 方法二：双指针

方法一没有利用数组 nums 1与 nums2已经被排序的性质。为了利用这一性质，我们可以使用双指针方法。这一方法将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中。

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int p1 = 0, p2 = 0;
        int[] sorted = new int[m+n];
        int cur;
        while(p1 < m || p2 < n){
            if(p1 == m){
                cur = nums2[p2++];
            }else if(p2 == n){
                cur = nums1[p1++];
            }else if(nums1[p1] < nums2[p2]){
                cur = nums1[p1++];
            }else{
                cur = nums2[p2++];
            }
            sorted[p1+p2-1] = cur;
        }
        for(int i = 0;i != m+n;i++){ //将sorted数组中元素复制到nums1中
            nums1[i] = sorted[i];
        }
    
    }
}

复杂度分析

时间复杂度：O(m+n)。
指针移动单调递增，最多移动 m+nm+n 次，因此时间复杂度为 O(m+n)。

空间复杂度：O(m+n)。
需要建立长度为 m+n 的中间数组 sorted。

方法三：逆向双指针

算法

方法二中，之所以要使用临时变量，是因为如果直接合并到数组 nums1中，nums1中的元素可能会在取出之前被覆盖。那么如何直接避免覆盖nums1中的元素呢？观察可知，nums1的后半部分是空的，可以直接覆盖而不会影响结果。因此可以指针设置为从后向前遍历，每次取两者之中的较大者放进nums1的最后面。

严格来说，在此遍历过程中的任意一个时刻，nums1数组中有 m-p1-1个元素被放入 nums1的后半部，nums2数组中有 n-p2-1个元素被放入 nums1的后半部，而在指针 p1的后面，nums1数组有 m+n-p1-1个位置。由于m+n-p1-1≥m−p1−1+n−p2−1等价于p2≥−1永远成立，因此 p1后面的位置永远足够容纳被插入的元素，不会产生 p1的元素被覆盖的情况。

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int p1 = m - 1,p2 = n - 1;
        int tail = m + n - 1;
        int cur;
        while(p1 >= 0 || p2 >= 0){
            if(p1 == -1){
                cur = nums2[p2--];
            }else if(p2 == -1){
                cur = nums1[p1--];
            }else if(nums1[p1] >= nums2[p2]){
                cur = nums1[p1--];
            }else{
                cur = nums2[p2--];
            }
            nums1[tail--] = cur;
        }
         
    }
}

复杂度分析

时间复杂度：O(m+n)。
指针移动单调递减，最多移动 m+n 次，因此时间复杂度为 O(m+n)。

空间复杂度：O(1)。
直接对数组 nums1原地修改，不需要额外空间。

三、合并两个链表

思路：

这道题中，链表的结点编号从 0 开始。将链表list1的第 a 个结点到第 b 个结点删除，则在删除的片段的前面有 a 个结点，编号依次为 0 到 a−1，在删除的片段的后面有 n - b - 1个结点，编号依次为 b+1 到n−1。被删除片段的前一个结点的编号是a−1，被删除片段的后一个结点的编号是b+1。由于 1≤a≤b<n−1，因此有a−1≤0 和b+1≤n−1，即被删除片段的前一个结点和后一个结点一定非空。

将编号为a−1 的结点记为beforeInsert，将编号b+1 的结点记为afterInsert。要将链表list2接在链表 list1被删除结点的位置，只要将list2的头结点接在beforeInsert 后面，将afterInsert 接在list2的尾结点后面即可。

由此可以得到如下解法：

从list1的头结点开始向后移动a−1 步，定位到beforeInsert；从list1的头结点开始向后移动b+1 步，定位到afterInsert；定位到list2的头结点和尾结点，分别记为start2和end2；令beforeInsert.next:=start2和end2.next:=afterInsert，完成合并操作。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {
        ListNode beforeInsert = list1, afterInsert = list1;
        for (int i = 1; i < a; i++) {
            beforeInsert = beforeInsert.next;
        }
        for (int i = 0; i < b + 1; i++) {
            afterInsert = afterInsert.next;
        }
        ListNode start2 = list2, end2 = list2;
        while (end2.next != null) {
            end2 = end2.next;
        }
        beforeInsert.next = start2;
        end2.next = afterInsert;
        return list1;
    }
}