当前位置:网站首页>【NOI模拟赛】伊莉斯elis(贪心,模拟)
【NOI模拟赛】伊莉斯elis(贪心,模拟)
2022-07-02 11:25:00 【DD(XYX)】
题面
1 s 512 m b _{_{\rm1\,s~~~~~512\,mb}} 1s 512mb



题解
我们会发现,任何时刻魔眼阈值最小的都是方阵的四个角之一,因此我们只需要考虑四个角上的魔眼就可以了。
判断是否有解可以贪心判断。
得到字典序最小的方案,可以每一步尝试向右+贪心判断是否有解。
那么怎么贪心判断呢?
注:以下为判断是否有解的贪心策略,并非最终输出的答案。
我们可以先把整个网格图分区:五芒星阵为魔眼区
由于魔眼每次减小的阈值等于曼哈顿距离,因此大方向肯定是越靠近魔眼区越好。
在 A 区域时,贪心地一路走到魔眼区左下角,中途怎么走随意,对魔眼区的影响相同。
在蓝色箭头区域,本着越靠近越好的原则,肯定是无脑往上走。
在 B 区域时,怎么走都无所谓了,对魔眼区的影响相同。
当你进入魔眼区的时候,就要麻烦点,
假设当前在魔眼区 ( x , y ) (x,y) (x,y) ,中途走出魔眼区肯定是不优的,所以肯定是一路走到 C C C 点,这一路对 A , C A,C A,C 的影响是相同的。出了 C C C 点之后就是随便走了,因此我们要尽量让 B , D B,D B,D 的阈值最小值最大。
左边的方案是对 B B B 最有利的、对 D D D 最有害的方案,右边的方案相反:
我们考虑调整法,从左边的方案调整到右边的方案,每次将一个“上右”变成“右上”,会刚好让 B B B 的阈值减少 2, D D D 的阈值增加 2 。所以,不论什么方案,对 B , D B,D B,D 的阈值贡献和是相等的,边界就是上述两种情况。我们可以 O ( 1 ) O(1) O(1) 贪心分配,使得最终 B , D B,D B,D 的阈值尽量平均。
代码实现算是一道模拟题了。
时间复杂度 O ( n ) O(n) O(n) 。既然是模拟,常数可以往大的写。
CODE
#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#pragma GCC optimize(2)
using namespace std;
#define MAXN (1<<16|5)
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define PR pair<int,int>
#define UIN unsigned int
int xchar() {
static const int maxn = 1000000;
static char b[maxn];
static int pos = 0,len = 0;
if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
if(pos == len) return -1;
return b[pos ++];
}
// #define getchar() xchar()
LL read() {
LL f = 1,x = 0;int s = getchar();
while(s < '0' || s > '9') {
if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
while(s >= '0' && s <= '9') {
x = (x<<1) + (x<<3) + (s^48);s = getchar();}
return f*x;
}
void putpos(LL x) {
if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
if(!x) {
putchar('0');return ;}
if(x<0) putchar('-'),x = -x;
return putpos(x);
}
void AIput(LL x,int c) {
putnum(x);putchar(c);}
int n,m,s,o,k;
int a,b,c;
LL A_,B_,L_,R_,t;
int Abs(int x) {
return x<0 ? -x:x;}
int dis(int x,int y,int a,int b) {
return Abs(a-x) + Abs(b-y);
}
LL sm(int l,int r) {
return (l+r) *1ll* (r-l+1) / 2;}
bool check(int x,int y,LL A,LL B,LL L,LL R) {
if(A > t || B > t || L > t || R > t) return 0;
if(x == n+1 && y == n) return 1;
if(x < a)
return check(a,b,A+sm(1,dis(x,y,a,b)),B+sm(c+c+1,dis(x,y,a+c,b+c)),
L+sm(c+1,dis(x,y,a,b+c)),R+sm(c+1,dis(x,y,a+c,b)));
if(x >= a+c && y >= b+c)
return check(n+1,n,A+sm(x-a+y-b,n-a+n-b),B+sm(x-a-c+y-b-c,n-a-c+n-b-c),
L+sm(x+y-a-b-c,n+n-a-b-c),R+sm(x+y-a-b-c,n+n-a-b-c));
if(x <= a+c && y < b)
return check(x,b,A+sm(x-a+1,dis(x,y,a,b)),B+sm(a+c-x+c+1,dis(x,y,a+c,b+c)),
L+sm(dis(x,b-1,a,b+c),dis(x,y,a,b+c)),R+sm(a+c-x+1,dis(x,y,a+c,b)));
if(x > a+c && y < b)
return check(x,b,A+sm(x-a+1,dis(x,y,a,b)),B+sm(x-a+1,dis(x,y,a,b)),
L+sm(dis(x,b-1,a,b+c),dis(x,y,a,b+c)),R+sm(x-a-c+1,dis(x,y,a+c,b)));
if(x > a+c && y < b+c)
return check(x,b+c,A+sm(dis(x,y,a,b),dis(x,b+c-1,a,b)),B+sm(dis(x,b+c-1,a+c,b+c),dis(x,y,a+c,b+c)),
L+sm(dis(x,b+c-1,a,b+c),dis(x,y,a,b+c)),R+sm(dis(x,y,a+c,b),dis(x,b+c-1,a+c,b)));
A += sm(dis(x,y,a,b),c+c); B += sm(0,dis(x,y,a+c,b+c));
LL sl = sm(x-a,dis(x,y,a,b+c)) + sm(x-a+1,c);
L += sl; R += sm(y-b,dis(x,y,a+c,b)) + sm(y-b+1,c);
LL ad = sm(dis(x,y,a,b+c),dis(a+c,y,a,b+c)) + sm(c,dis(a+c,y,a,b+c)-1) - sl;
if(L+ad <= R+2) L += ad;
else if(R+ad <= L+2) R += ad;
else {
if(L > R) swap(L,R);
LL nb = R-L - ((R-L)&1); L += nb; ad -= nb;
if(ad & 3) ad -= 2,L += 2;
L += ad>>1; R += ad>>1;
}
return check(a+c+1,b+c,A,B,L,R);
}
int main() {
freopen("elis.in","r",stdin);
freopen("elis.out","w",stdout);
n = read(); t = read();
a = read(); b = read(); c = read()-1;
int x = 1,y = 1;
if(!check(x+1,y,0,0,0,0) && !check(x,y+1,0,0,0,0)) return printf("Again\n"),0;
while(x < n || y < n) {
if(x < n && check(x+1,y,A_,B_,L_,R_)) x ++,putchar('R');
else y ++,putchar('U');
A_ += dis(x,y,a,b); B_ += dis(x,y,a+c,b+c);
L_ += dis(x,y,a,b+c); R_ += dis(x,y,a+c,b);
} ENDL;
return 0;
}
这好像是几年前的题了吧
边栏推荐
- String matching problem
- < schéma de développement de la machine d'exercice oral > machine d'exercice oral / trésor d'exercice oral / trésor de mathématiques pour enfants / lecteur LCD de calculatrice pour enfants IC - vk1621
- php链表创建和遍历
- Stm32-dac Experiment & high frequency DAC output test
- Advanced C language (realize simple address book)
- QT new project
- STM32标准固件库函数名记忆(二)
- C#代码审计实战+前置知识
- mathML转latex
- Yyds dry goods inventory software encryption lock function
猜你喜欢
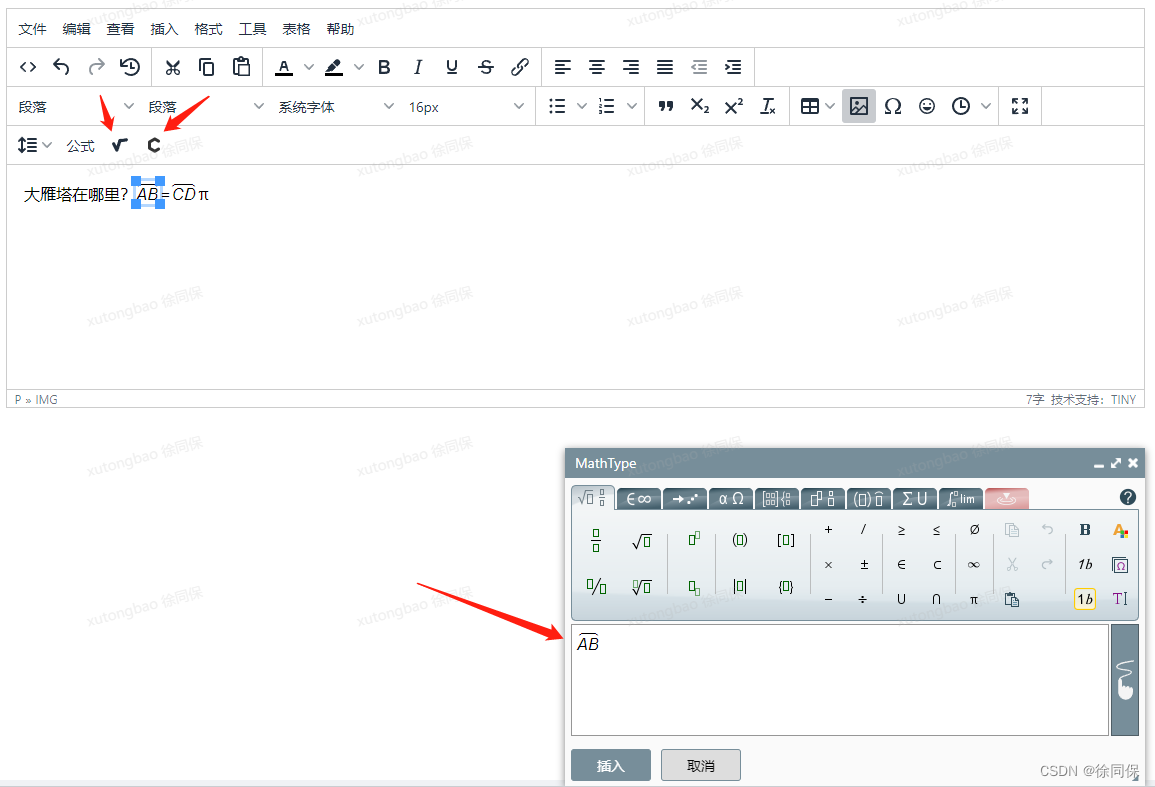
富文本编辑器添加矢量公式(MathType for TinyMCE ,可视化添加)

Fabric.js 缩放画布

【apipost】使用教程

socket(套接字)与socket地址

什么是 eRDMA?丨科普漫画图解

Actual combat sharing of shutter screen acquisition

Thoroughly master prototype__ proto__、 Relationship before constructor (JS prototype, prototype chain)
Advanced C language (realize simple address book)

Makefile 分隔文件名与后缀

Fabric.js 上划线、中划线(删除线)、下划线
随机推荐
The use of TestNG, the testing framework (II): the use of TestNG XML
Yolov3 & yolov5 output result description
Uniapp automated test learning
php链表创建和遍历
< schéma de développement de la machine d'exercice oral > machine d'exercice oral / trésor d'exercice oral / trésor de mathématiques pour enfants / lecteur LCD de calculatrice pour enfants IC - vk1621
fatal: unsafe repository is owned by someone else 的解决方法
Daily learning 2
obsidian安装第三方插件——无法加载插件
Fabric. JS upper dash, middle dash (strikethrough), underline
taobao. trades. sold. Get query the transaction data that the seller has sold (according to the creation time), Taobao store sales order query API interface, Taobao R2 interface, Taobao oauth2.0 trans
info [email protected]: The platform “win32“ is incompatible with this module.
途家木鸟美团夏日折扣对垒,门槛低就一定香吗?
Obsidian installs third-party plug-ins - unable to load plug-ins
《可供方案开发》口算训练机/数学宝/儿童口算宝/智能数学宝 LCD液晶显示驱动IC-VK1622(LQFP64封装),原厂技术支持
没有从远程服务器‘‘映射到本地用户‘(null)/sa‘的远程用户‘sa‘及服务主密码解密错误的解决办法
uniapp自动化测试学习
Actual combat sharing of shutter screen acquisition
C语言高级用法--函数指针:回调函数;转换表
How kaggle uses utility script
Daily learning 3