当前位置:网站首页>Jordan decomposition example of matrix
Jordan decomposition example of matrix
2022-07-02 07:22:00 【Drizzle】
Matrix Jordan Explode instance
Matrix Jordan decompose : Standard + Transformation matrix
〇、 subject
The subject comes from 《 Computer Science Computing 》 The second edition , Editor Zhang Hongwei , Golden sun , Shi Jilin , Dong Bo . book P86 The first 12 topic .
O matrix A = [ 4 − 1 − 1 0 4 0 − 2 0 0 0 2 0 0 0 6 1 ] A= \left[\begin{array}{cccc} 4 & -1 & -1 & 0\\ 4 & 0 & -2 & 0\\ 0 & 0 & 2 & 0 \\ 0 & 0 & 6 & 1 \end{array}\right] A=⎣⎢⎢⎡4400−1000−1−2260001⎦⎥⎥⎤ Of Jordan decompose .
One 、 Find its Jordan Standard
Calculation d e t ( λ I − A ) = ∣ λ − 4 1 1 0 − 4 λ 2 0 0 0 λ − 2 0 0 0 − 6 λ − 1 ∣ det(\lambda I - A) = \left|\begin{array}{cccc} \lambda - 4 & 1 & 1 & 0\\ -4 & \lambda & 2 & 0\\ 0 & 0 & \lambda - 2 & 0\\ 0 & 0 & -6 & \lambda - 1\\ \end{array}\right| det(λI−A)=∣∣∣∣∣∣∣∣λ−4−4001λ0012λ−2−6000λ−1∣∣∣∣∣∣∣∣.
The eigenvalue of the solution is λ 1 = 1 \lambda _1 = 1 λ1=1( A multiplicity of algebra ), λ 2 = 2 \lambda _2 = 2 λ2=2( Triple algebraic multiplicity 、 Order ).
Calculation r a n k ( λ 2 I − A ) = 2 rank(\lambda _2 I - A) = 2 rank(λ2I−A)=2, obtain λ 2 \lambda _2 λ2 The geometric multiplicity of is 2, Namely its Jordan The number of blocks is 2, Because the order is 3, You can get two of them Jordan The block must be 1 + 2 1 + 2 1+2 The format of .
Available Jordan The standard type is : J = [ 1 0 0 0 0 2 0 0 0 0 2 1 0 0 0 2 ] J= \left[\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 2 & 0 & 0\\ 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 2 \end{array}\right] J=⎣⎢⎢⎡1000020000200012⎦⎥⎥⎤.
Two 、 Find its transformation matrix T
By definition A ⋅ ( T 1 , T 2 , T 3 , T 4 ) = ( T 1 , T 2 , T 3 , T 4 ) ⋅ J A \cdot (T_1, T_2, T_3, T_4) = (T_1, T_2, T_3, T_4) \cdot J A⋅(T1,T2,T3,T4)=(T1,T2,T3,T4)⋅J
Two 、 One 、 The first eigenvalue
The following solution , Superscript indicates the block serial number , Subscript indicates the number in the block .
about λ 1 = 1 \lambda _1 = 1 λ1=1, Find its linearly independent eigenvector .
A ⋅ t 1 = λ 1 ⋅ t 1 A \cdot t^1 = \lambda _1 \cdot t^1 A⋅t1=λ1⋅t1, One vector of the solution is t 1 = ( 0 , 0 , 0 , 1 ) T t^1 = (0, 0, 0, 1)^T t1=(0,0,0,1)T, Because it is a geometric multiplicity , You can do it directly Jordan Head of chain .
Two 、 Two 、 The second eigenvalue
Empathy , solve equations ( A − λ 2 I ) ⋅ t 2 = 0 (A - \lambda _2I) \cdot t^2 = 0 (A−λ2I)⋅t2=0
[ 2 − 1 − 1 0 4 − 2 − 2 0 0 0 0 0 0 0 6 1 ] ⋅ t 2 = 0 \left[\begin{array}{cccc} 2 & -1 & -1 & 0\\ 4 & -2 & -2 & 0\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 6 & 1 \end{array}\right] \cdot t^2 = 0 ⎣⎢⎢⎡2400−1−200−1−2060001⎦⎥⎥⎤⋅t2=0
Solution : t 1 3 = t 1 2 = ( 1 , 1 , 1 , 6 ) T , t 2 3 = t 2 2 = ( 0 , 0 , 1 , 6 ) T t^3_1 = t^2_1 = (1, 1, 1, 6)^T,t^3_2 = t^2_2 = (0, 0, 1, 6)^T t13=t12=(1,1,1,6)T,t23=t22=(0,0,1,6)T
Previously known λ 2 = 2 \lambda _2 = 2 λ2=2 It's divided into two parts , The order of a piece ( chain length ) by 1, The order of a piece is 2.
Here we can directly get the order 1 Get the head of the chain , t 2 = ( 1 , 1 , 1 , 6 ) T t^2 = (1, 1, 1, 6)^T t2=(1,1,1,6)T
For chain length 2 Chain , In order to ensure that the second ring can be launched from the head of the chain , That is, the following equation has a solution . ( y by chain The first t 1 3 , z by The first Two Ring t 2 3 ) (y For the head of the chain t^3_1,z For the second ring t^3_2) (y by chain The first t13,z by The first Two Ring t23)
( A − λ 2 I ) ⋅ z = y ( A - \lambda _2 I ) \cdot z = y (A−λ2I)⋅z=y
Make y = k 1 ⋅ t 1 3 + k 2 ⋅ t 2 3 = ( k 1 + k 2 , 2 k 1 − k 2 , k 2 , 6 k 2 ) T y = k_1\cdot t^3_1 + k_2\cdot t^3_2 = (k_1 + k_2, 2k_1 - k_2, k_2, 6k_2)^T y=k1⋅t13+k2⋅t23=(k1+k2,2k1−k2,k2,6k2)T
The condition of its solution is r ( A − λ 2 I ) = r ( ( A − λ 2 I ) ∣ y ) r( A - \lambda _2 I ) = r( \space ( A - \lambda _2 I ) \space | y ) r(A−λ2I)=r( (A−λ2I) ∣y).
Obtainable k 2 = 0 , k 1 = 1 k_2 = 0, k_1 = 1 k2=0,k1=1, namely y = ( 1 , 2 , 0 , 0 ) T y = (1, 2, 0, 0)^T y=(1,2,0,0)T, Substituting into the original equation , You can get z = ( 1 , 1 , 0 , 0 ) T z = (1, 1, 0, 0)^T z=(1,1,0,0)T.
The transformation matrix obtained by synthesis is : T = [ 0 1 1 1 0 1 2 1 0 1 0 0 1 6 0 0 ] T= \left[\begin{array}{cccc} 0 & 1 & 1 & 1\\ 0 & 1 & 2 & 1\\ 0 & 1 & 0 & 0 \\ 1 & 6 & 0 & 0 \end{array}\right] T=⎣⎢⎢⎡0001111612001100⎦⎥⎥⎤.
3、 ... and 、 Scientific checking
Use an online calculator Cloud operator , verification A = T J T − 1 A = TJT^{-1} A=TJT−1.
Correct checking calculation , The following is its T − 1 T^{-1} T−1 value .
T − 1 = [ 0 0 − 6 1 0 0 1 0 − 1 1 0 0 2 − 1 − 1 0 ] T^{-1} =\left[\begin{array}{cccc} 0 & 0 & -6 & 1\\ 0 & 0 & 1 & 0\\ -1 & 1 & 0 & 0 \\ 2 & -1 & -1 & 0 \end{array}\right] T−1=⎣⎢⎢⎡00−12001−1−610−11000⎦⎥⎥⎤
边栏推荐
- Ingress Controller 0.47.0的Yaml文件
- mapreduce概念和案例(尚硅谷学习笔记)
- ORACLE 11G利用 ORDS+pljson来实现json_table 效果
- 使用Matlab实现:Jacobi、Gauss-Seidel迭代
- Oracle EBS数据库监控-Zabbix+zabbix-agent2+orabbix
- How to efficiently develop a wechat applet
- TCP attack
- 类加载器及双亲委派机制
- 2021-07-19c CAD secondary development creates multiple line segments
- @Transational踩坑
猜你喜欢

第一个快应用(quickapp)demo

How to efficiently develop a wechat applet

Oracle 11g uses ords+pljson to implement JSON_ Table effect
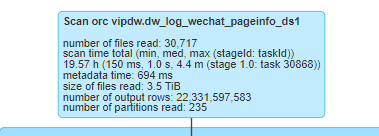
spark sql任务性能优化(基础)
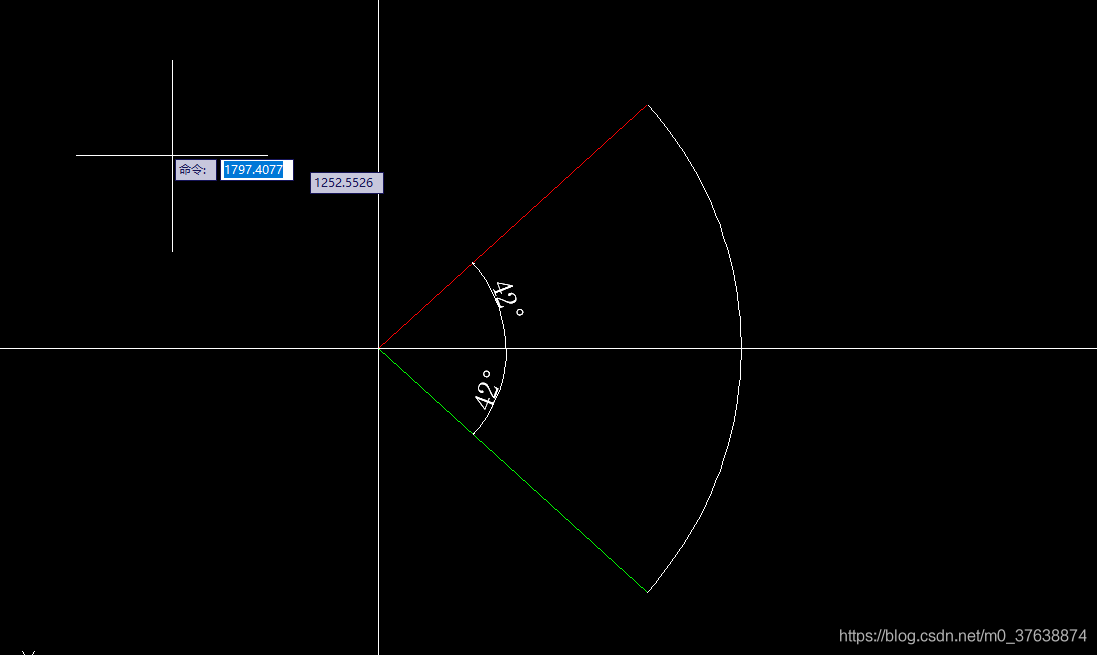
2021-07-05c /cad secondary development create arc (4)
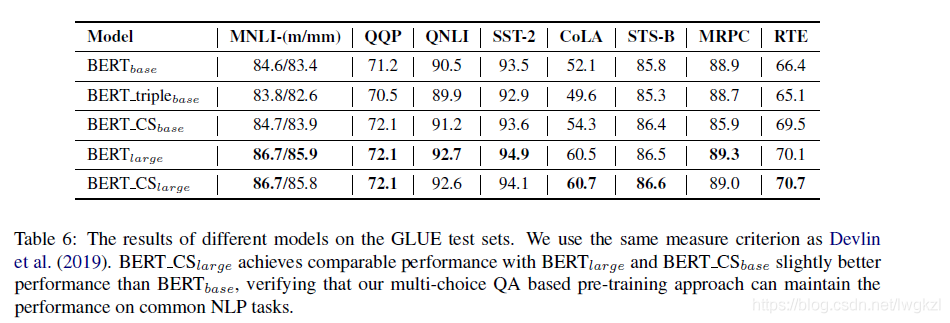
【BERT,GPT+KG调研】Pretrain model融合knowledge的论文集锦

Ding Dong, here comes the redis om object mapping framework

Ceaspectuss shipping company shipping artificial intelligence products, anytime, anywhere container inspection and reporting to achieve cloud yard, shipping company intelligent digital container contr

类加载器及双亲委派机制

ORACLE EBS ADI 开发步骤
随机推荐
sparksql数据倾斜那些事儿
2021-07-19c CAD secondary development creates multiple line segments
ORACLE 11G利用 ORDS+pljson来实现json_table 效果
Agile development of software development pattern (scrum)
allennlp 中的TypeError: Object of type Tensor is not JSON serializable错误
Yolov5 practice: teach object detection by hand
Get the uppercase initials of Chinese Pinyin in PHP
图解Kubernetes中的etcd的访问
Sqli Labs clearance summary - page 2
ssm人事管理系统
view的绘制机制(一)
Network security -- intrusion detection of emergency response
CAD secondary development object
User login function: simple but difficult
Two table Association of pyspark in idea2020 (field names are the same)
Pyspark build temporary report error
【调参Tricks】WhiteningBERT: An Easy Unsupervised Sentence Embedding Approach
【信息检索导论】第二章 词项词典与倒排记录表
ARP attack
ORACLE APEX 21.2安装及一键部署