当前位置:网站首页>【特征选取】计算数据点曲率
【特征选取】计算数据点曲率
2022-08-03 05:10:00 【xiaozheng123121】
0、引言
为更好地发挥 NURBS 曲线在表达原始数据曲线形状特征方面的优势,非均匀 B 样条插值仍需对原始密集刀位数据点合理地选取特征点。
由于数据点的曲率信息能够很好地反映原始数据曲线的形状特征,把数据点与曲率关联起来进行形状特征点的选取,可以更好地表达原始数据曲线的形状特征。
NURBS 曲线的基本定义
一条 ρ \rho ρ 次 NURBS 曲线定义为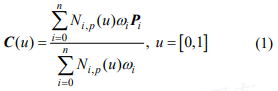
一、计算数据点曲率
采用相邻 3 个数据点形成近似圆弧的方法进行各原始数据点曲率的求解。 如图 1 所示,设原始数据点的个数为 t + 1 t +1 t+1, 其中 i i i 个数据点 Q i Q_i Qi 对应的曲率半径为 p i ( i = 0 , 1 , … , t ) p_i (i=0,1,…,t) pi(i=0,1,…,t),其近似求解公式为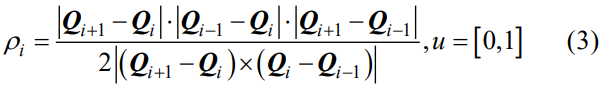
则第 i i i 个数据点 Q i Q_i Qi 处对应的曲率为
k i = 1 ρ i ( 4 ) k_i=\frac{1}{\rho_i} \qquad\qquad(4) ki=ρi1(4)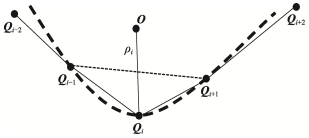
二、曲率段间分段点位置的确定
原始数据曲线按照曲率大小可划分为若干大曲率段和若干小曲率段。大曲率段曲线的弯曲程度较大,应选取较多的特征点才能更好地表达曲线的弯曲特征。小曲率段曲线相对而言则比较平直,选取较少的特征点便可较好地表达曲线的特征。 可见,不同大小曲率段选取的特征点数也会有所差别,有必要研究曲线按曲率进行分段的方法,准确确定出各曲率段间临界分段点的位置。
2.1 分段点位置的初确定
当第 i i i 个数据点 Q i Q_i Qi 对应的曲率 k i k_i ki 与邻近的数据点曲率之间满足如下初确定条件之一时,
( 1 ) k i − j > k i , j = 1 , 2 , 3 ; \ \ \ (1)\ \ \ k_{i-j}>k_i,\ \ j=1,2,3; (1) ki−j>ki, j=1,2,3;
( 2 ) k i + j > k i , j = 1 , 2 , 3. \ \ \ (2)\ \ \ k_{i+j}>k_i, \ \ j=1,2,3. (2) ki+j>ki, j=1,2,3.
则可以将 Q i Q_i Qi 作为曲线按曲率分段的初确定分段点。
但是考虑原始数据曲线存在曲率跳跃的情况,仅满足上述一个条件尚不足以保证 Q i Q_i Qi 两侧邻近数据点中的一侧数据点曲率远大于另一侧数据点的曲率。因此,还需针对不同情况辅以其他约束条件,以保证分段点的准确性。
2.2 分段点位置的终确定
当第 i i i 个数据点 Q i Q_i Qi 对应的曲率 k i k_i ki 满足条件 (1) 时,记,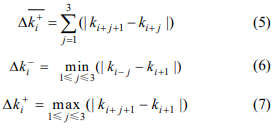
其中, Δ k i + ‾ \Delta{\overline{k_i^+}} Δki+表示向前曲率差分之和; Δ k i \Delta{k_i} Δki 表示曲率差分极值;符号“+”与“-”分别表示向前与向后差分运算。
如果满足 Δ k i − > Δ k i + ‾ \Delta{k_i^-}>\Delta{\overline{k_i^+}} Δki−>Δki+,且满足 H Δ k i + < k ‾ H\Delta{k_i^+}< \overline{k} HΔki+<k,则可以将曲率值 k i k_i ki 对应的数据点 Q i Q_i Qi 作为终确定的分段点,其中, H H H 为常数, H H H 通常取值为 2 2 2~ 3 3 3; k ‾ \overline k k 为所有数据点曲率的平均值。
同样, 当第 i i i 个数据点 Q i Q_i Qi 对应的曲率 k i k_i ki 满足条件(2)时, 记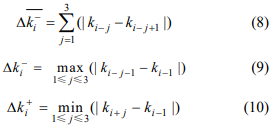
参考资料
[1] 曲率自适应条件下特征点选取的非均匀 B 样条曲线插值方法
[2] Nurbs曲线详解 2018.9
边栏推荐
- Flink state
- Concepts and Methods of Exploratory Testing
- Exception(异常) 和 Error(错误)区别解析
- Where is the value of testers
- Shell conditional statement judgment
- js implements a bind function
- Bubble sort in c language structure
- 13.< tag-动态规划和回文字串>lt.647. 回文子串 + lt.516.最长回文子序列
- [Fine talk] Using native js to implement todolist
- 信息编码、存储压缩与密码学
猜你喜欢
Install IIS services (Internet Information Services (Internet Information Services, abbreviated IIS, Internet Information Services)

Apache DolphinScheduler版本2.0.5分布式集群的安装
idea uses @Autowired annotation to explain the reasons and solutions

Tag stack - stack monotonically preparatory knowledge - lt. 739. The daily temperature

传说中可“免费白拿”的无线路由器 - 斐讯 K2 最简单刷 breed 与第三方固件教程
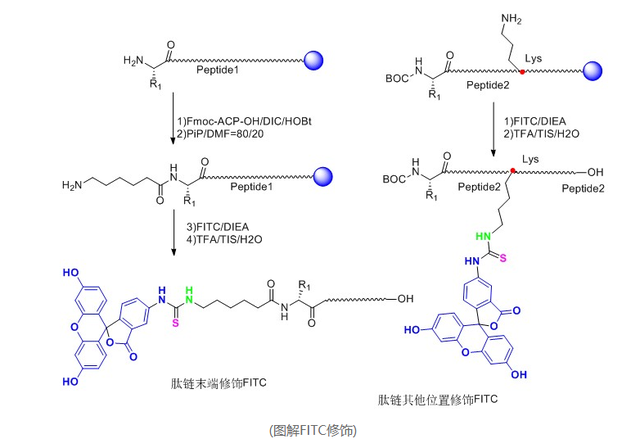
Fluorescent marker peptides FITC/AMC/FAM/Rhodamine TAMRA/Cy3 / Cy5 / Cy7 - Peptide
Pr第四次培训笔记
web安全-PHP反序列化漏洞
CAD有生僻字如何打出来、如何提交软件相关问题或建议?

VSO Downloader Ultimate 5.0.1.45 中文多语免费版 在线视频下载工具
随机推荐
ss-5.consul服务端+生产者+消费者
Junit
shell脚本循环语句
网络流媒体下载的 10 种方法(以下载 Echo 音乐为例)
IO process thread -> thread -> day5
Practical application of WebSocket
【Biotin Azide|cas:908007-17-0】Price_Manufacturer
Alienware上线首个数字时装AR试穿体验
Djiango第二次培训
Object类与常用API
web安全-SSTI模板注入漏洞
Peptides mediated PEG DSPE of phospholipids, targeted functional materials - PEG - RGD/TAT/NGR/APRPG
阿里云对象存储oss私有桶生成链接
typescript41-class类的私有修饰符
13.
lt.647. Palindromic substring + lt.516. Longest palindrome subsequence The problem that the rosbag tool plotjuggler cannot open rosbag
Djiango第四次培训笔记
Lambda表达式案例
4.如何避免缓存穿透、缓存击穿、缓存雪崩
Create a tree structure