当前位置:网站首页>[linear algebra] determinant of order 1.3 n
[linear algebra] determinant of order 1.3 n
2022-07-06 22:18:00 【Michael_ Lzy】
First study the third-order determinant :
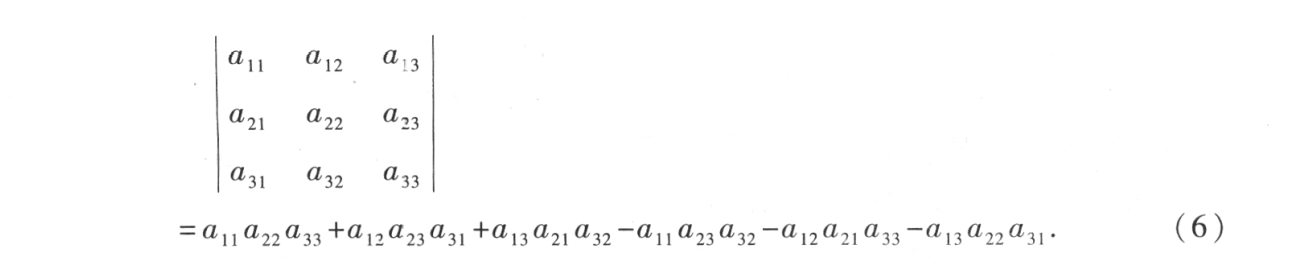
Easy to see :
1) (6) Each term of the formula is exactly the product of three elements , These three elements are on different lines 、 Different columns .
Therefore, any item can be written as  .
.
The first subscript of each item here ( Line mark ) Arrange in standard order 123.
namely :![]()
And the second subscript of each item ( Column mark ), Line up p1p2p3, It is 1,2,3 An arrangement of three numbers . This arrangement shares 6 Kind of , Corresponding (6) Formula Co containing 6 term .
2) The sign of each item is compared with the arrangement of column marks
The trinomial column with a positive sign is 123,231,312.( Are even permutations )
![]()
The arrangement of three column labels with minus sign is 132,213,321.( They are all odd permutations )
The calculation shows that The first three permutations are even permutations , The last three permutations are all odd permutations .
therefore , The sign of each item can be expressed as  , among t by Column label arrangement Of Reverse order number .
, among t by Column label arrangement Of Reverse order number .
All in all , The third-order determinant can be written as :
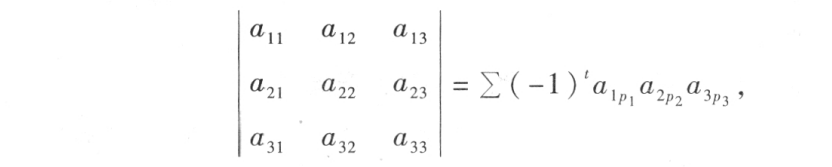
among t To arrange p1p2p3 In reverse order ,∑ It means to sum all sorts of permutations .
Generalize determinant to general form :
Equipped with  Number , Line up n That's ok n A list of numbers :
Number , Line up n That's ok n A list of numbers :
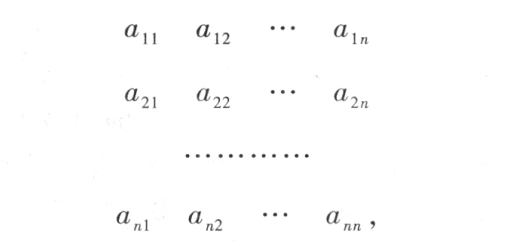
Make the table in different rows and columns n The product of numbers , And prefixed with symbols  , Get the shape of
, Get the shape of
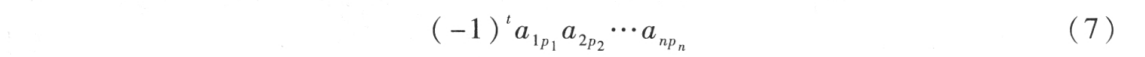
among p1p2...pn For natural Numbers 1,2...,n An arrangement of ,t The number in reverse order for this arrangement .
Because this arrangement has n! individual , Thus, it is shaped like (7) The terms of formula have n! term .
All this n! Algebraic sum of terms
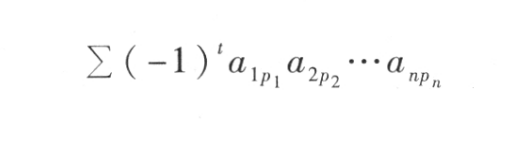
be called n Step determinant , Write it down as :

A shorthand det( ), Among them
), Among them  For determinant (i,j) element .
For determinant (i,j) element .
When n=1 when , First order determinant |a|=a, Be careful not to confuse with the absolute value number .
All the elements below are diagonals 0 The determinant of is called Upper triangular determinant .
The elements above the main diagonal are 0 The determinant of is called Lower triangular determinant .
The elements above and below the main diagonal are 0 The determinant of is called Diagonal determinants .
边栏推荐
猜你喜欢
图像的spatial domain 和 frequency domain 图像压缩
数据处理技巧(7):MATLAB 读取数字字符串混杂的文本文件txt中的数据
zabbix 代理服务器 与 zabbix-snmp 监控
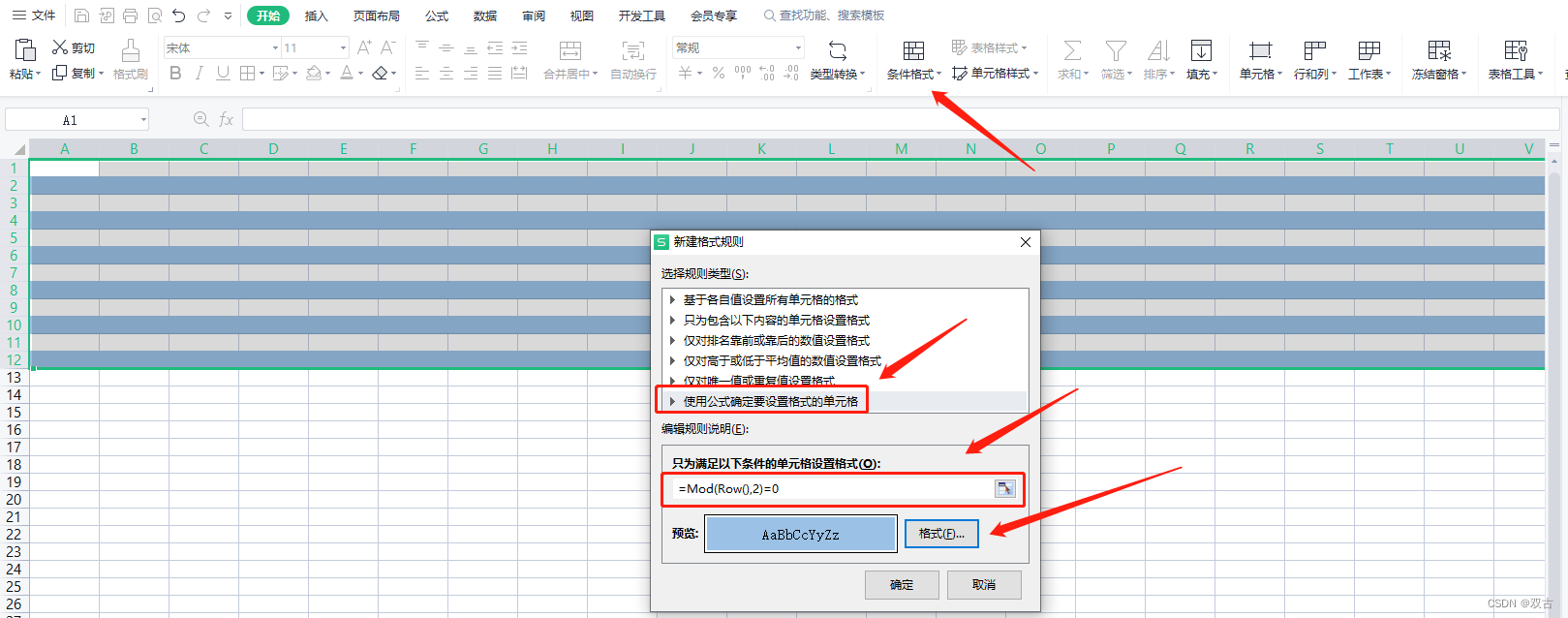
嵌入式常用计算神器EXCEL,欢迎各位推荐技巧,以保持文档持续更新,为其他人提供便利

小常识:保险中的“保全”是什么?
Memorabilia of domestic database in June 2022 - ink Sky Wheel

GPS从入门到放弃(十七) 、对流层延时
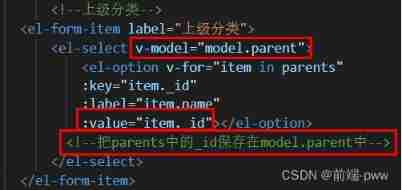
Management background --5, sub classification

GPS from getting started to giving up (16), satellite clock error and satellite ephemeris error

2022年6月国产数据库大事记-墨天轮
随机推荐
Kohana database
Assembly and interface technology experiment 5-8259 interrupt experiment
Force deduction question 500, keyboard line, JS implementation
GPS from getting started to giving up (16), satellite clock error and satellite ephemeris error
第3章:类的加载过程(类的生命周期)详解
Management background --5, sub classification
3DMax指定面贴图
【sciter Bug篇】多行隐藏
Realization of epoll reactor model
Insert sort and Hill sort
C#实现水晶报表绑定数据并实现打印4-条形码
Support multiple API versions in flask
RESNET rs: Google takes the lead in tuning RESNET, and its performance comprehensively surpasses efficientnet series | 2021 arXiv
[MySQL] online DDL details
Shell product written examination related
Huawei has launched attacks in many industries at the same time, and its frightening technology has made European and American enterprises tremble
Unity3d Learning Notes 6 - GPU instantiation (1)
Oracle control file and log file management
3DMAX assign face map
【MySQL】Online DDL详解