当前位置:网站首页>二叉(搜索)树的最近公共祖先 ●●
二叉(搜索)树的最近公共祖先 ●●
2022-07-06 14:17:00 【chenyfan_】
236. 二叉树的最近公共祖先 ●●
描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例
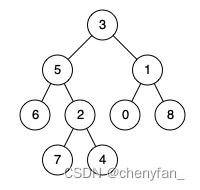
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
题解
1. 后序遍历(回溯)
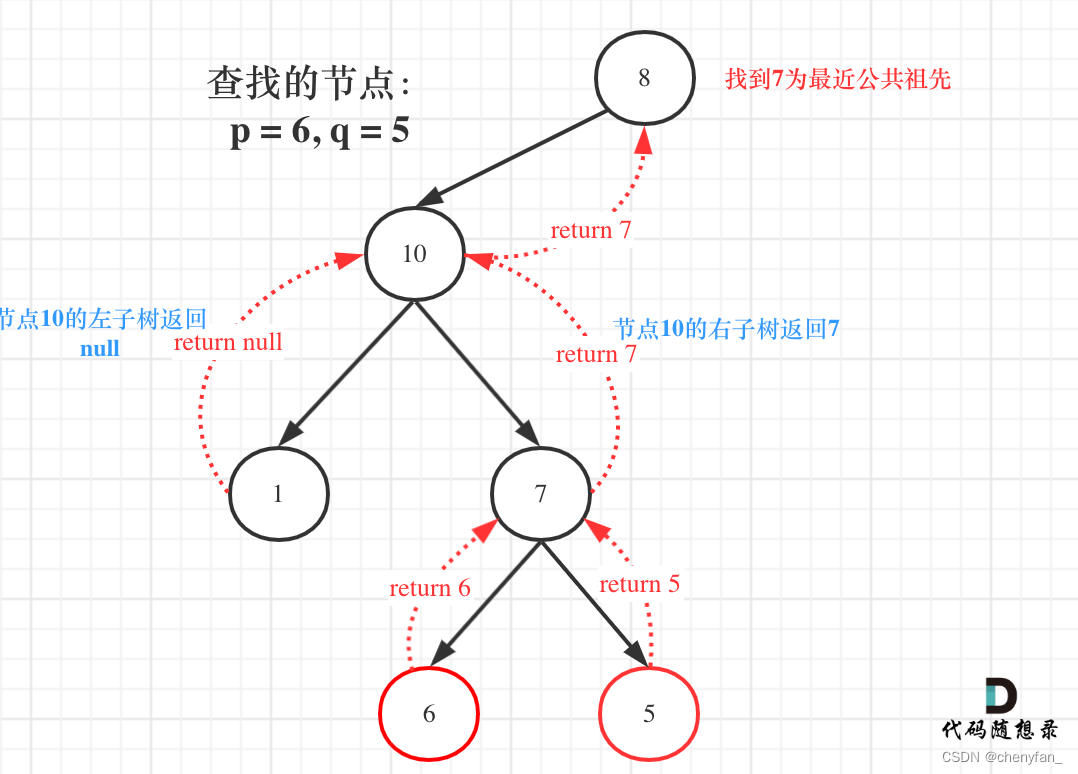
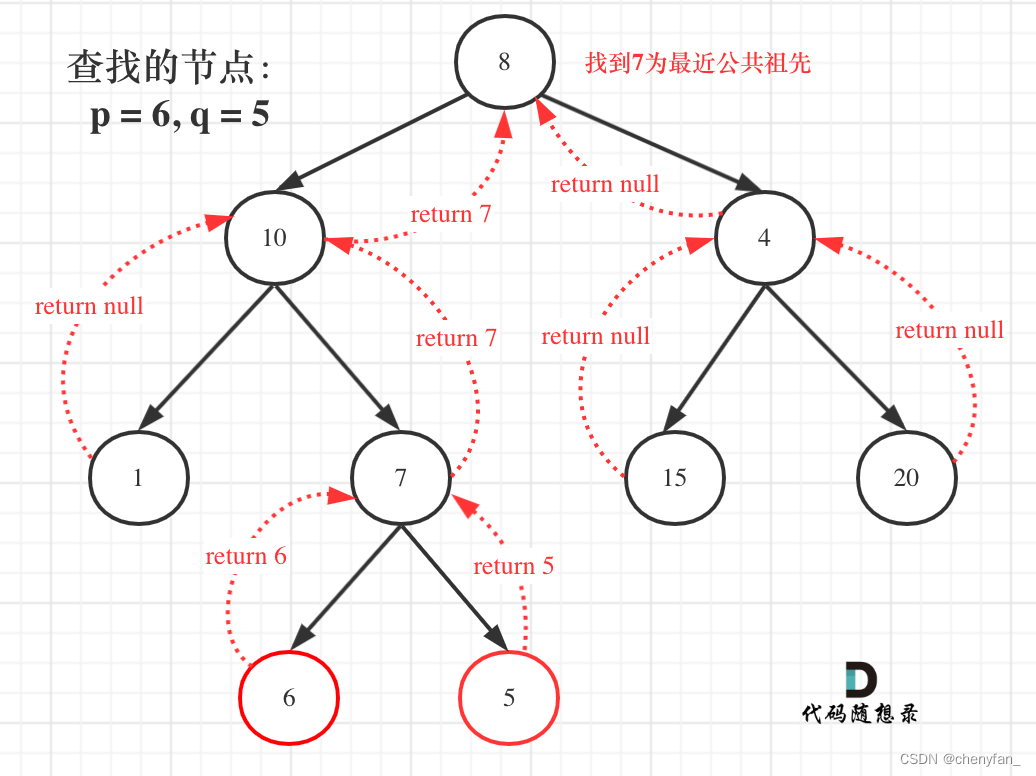
最容易想到的第一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点 p 和 q 的最近公共祖先。
但是还存在第二个情况,就是节点本身 p(q),它拥有一个子孙节点 q§。
使用后序遍历,回溯的过程,就是从低向上遍历节点,一旦发现满足第一种情况的节点,就是最近公共节点了。
但是如果p或者q本身就是最近公共祖先呢?
其实只需要找到一个节点是 p 或者 q 的时候,直接返回当前节点,无需继续递归子树。如果接下来的(向上的)遍历中找到了后继节点(父辈节点)满足第一种情况则修改返回值为后继节点,否则,继续返回已找到的节点即可。
在递归函数有返回值的情况下:
如果要搜索一条边,递归函数返回值不为空的时候,立刻返回;
if (递归函数(root->left)) return ;
if (递归函数(root->right)) return ;
如果要搜索整个树,直接用一个变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯)。
left = 递归函数(root->left);
right = 递归函数(root->right);
left与right的逻辑处理;
- 时间复杂度 O(N) : 其中 N 为二叉树节点数;最差情况下,需要递归遍历树的所有节点。
- 空间复杂度 O(N) : 最差情况下,递归深度达到 N ,系统使用 O(N) 大小的额外空间。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == q || root == p || root == NULL) return root; // 判断当前节点
TreeNode* left = lowestCommonAncestor(root->left, p, q); // 遍历左子树
TreeNode* right = lowestCommonAncestor(root->right, p, q); // 遍历右子树
if(left != NULL && right != NULL){
return root; // 左右子树都有返回值,则当前为最近公共祖先
}else if(left != NULL){
return left; // 只有左子树有返回值
}else if(right != NULL){
return right; // 只有右子树有返回值
}
return NULL;
}
};
235. 二叉搜索树的最近公共祖先 ●
描述
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例
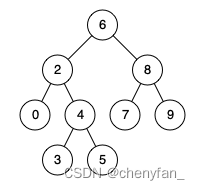
p = 4, q = 7;输出: 6
p = 2, q = 4;输出: 2
题解
与普通二叉树不同,二叉搜索树是有序的,只要从上到下遍历的时候,cur 节点是数值在 [p, q] 区间中则说明该节点 cur 就是最近公共祖先了,而且不需要遍历整棵树,找到结果直接返回。
1. 层序遍历 队列 迭代
未根据节点的大小进行搜索方向的判断调整,效率较低。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
int Min = min(p->val, q->val);
int Max = max(p->val, q->val);
queue<TreeNode*> que;
que.push(root);
while(!que.empty()){
TreeNode* curr = que.front();
que.pop();
if(curr->val <= Max && curr->val >= Min) return curr;
if(curr->left) que.push(curr->left);
if(curr->right) que.push(curr->right);
}
return NULL;
}
};
2. 前序遍历
根据节点的大小进行搜索方向的判断调整。
当节点值同时大于p、q值时,往左子树搜索;
当节点值同时小于p、q值时,往右子树搜索;
否则节点值在区间内,满足条件,直接返回。
递归
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == NULL) return NULL;
if(root->val > p->val && root->val > q->val){
// 中
TreeNode* left = lowestCommonAncestor(root->left, p, q); // 左
if(left != NULL) return left;
}
if(root->val < p->val && root->val < q->val){
TreeNode* right = lowestCommonAncestor(root->right, p, q); // 右
if(right != NULL) return right;
}
return root; // 节点值在区间内
}
};
迭代
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
while(root != NULL){
if(root->val > p->val && root->val > q->val){
root = root->left; // 往左
}else if(root->val < p->val && root->val < q->val){
root = root->right; // 往右
}else return root; // 节点值在区间内
}
return NULL;
}
};
边栏推荐
- 2500 common Chinese characters + 130 common Chinese and English characters
- MySQL related terms
- LeetCode:1189. The maximum number of "balloons" -- simple
- Run the deep network on PI and Jetson nano, and the program is killed
- [Chongqing Guangdong education] Tianjin urban construction university concrete structure design principle a reference
- Oracle Performance Analysis 3: introduction to tkprof
- 1292_ Implementation analysis of vtask resume() and xtask resume fromisr() in freeros
- What can one line of code do?
- GPS from entry to abandonment (XIV), ionospheric delay
- Oracle control file and log file management
猜你喜欢
![[Chongqing Guangdong education] Tianjin urban construction university concrete structure design principle a reference](/img/61/976c7d86ab3b2df5f5af3beefbf547.png)
[Chongqing Guangdong education] Tianjin urban construction university concrete structure design principle a reference
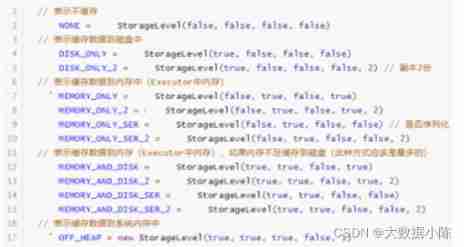
Persistence / caching of RDD in spark
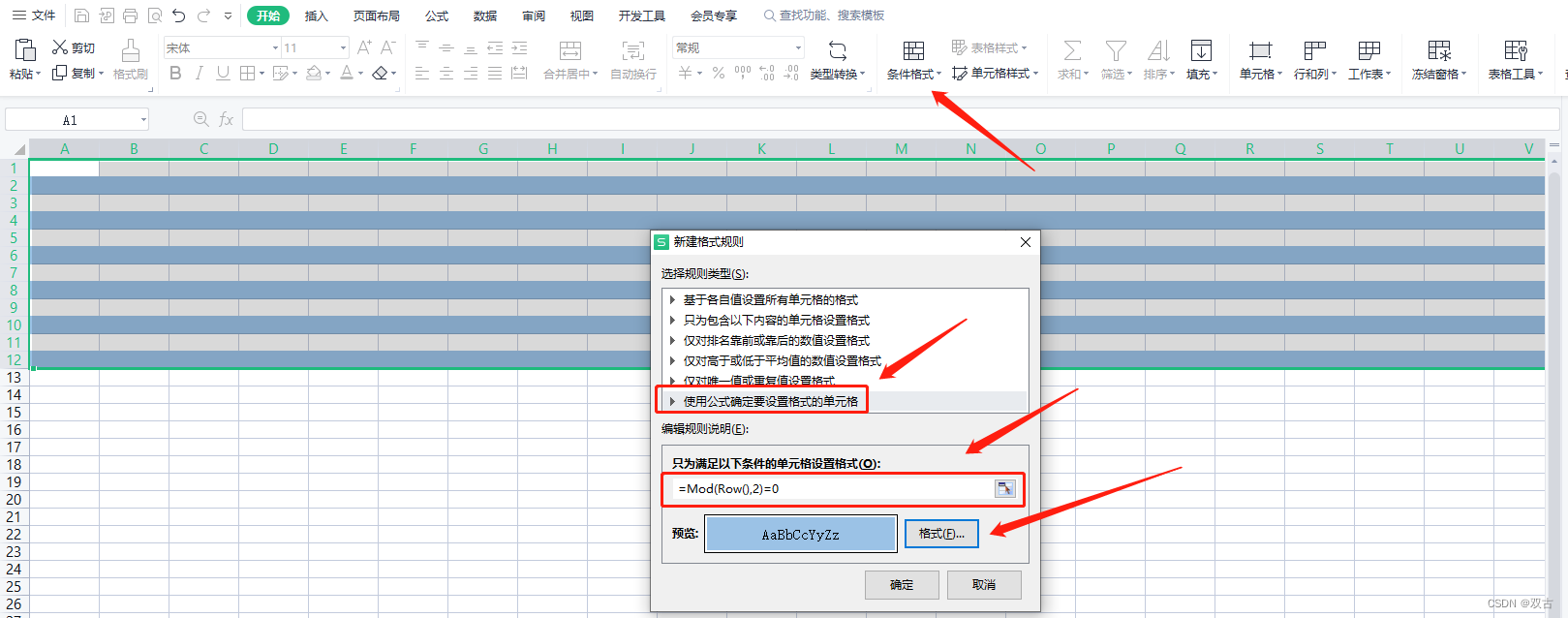
Embedded common computing artifact excel, welcome to recommend skills to keep the document constantly updated and provide convenience for others
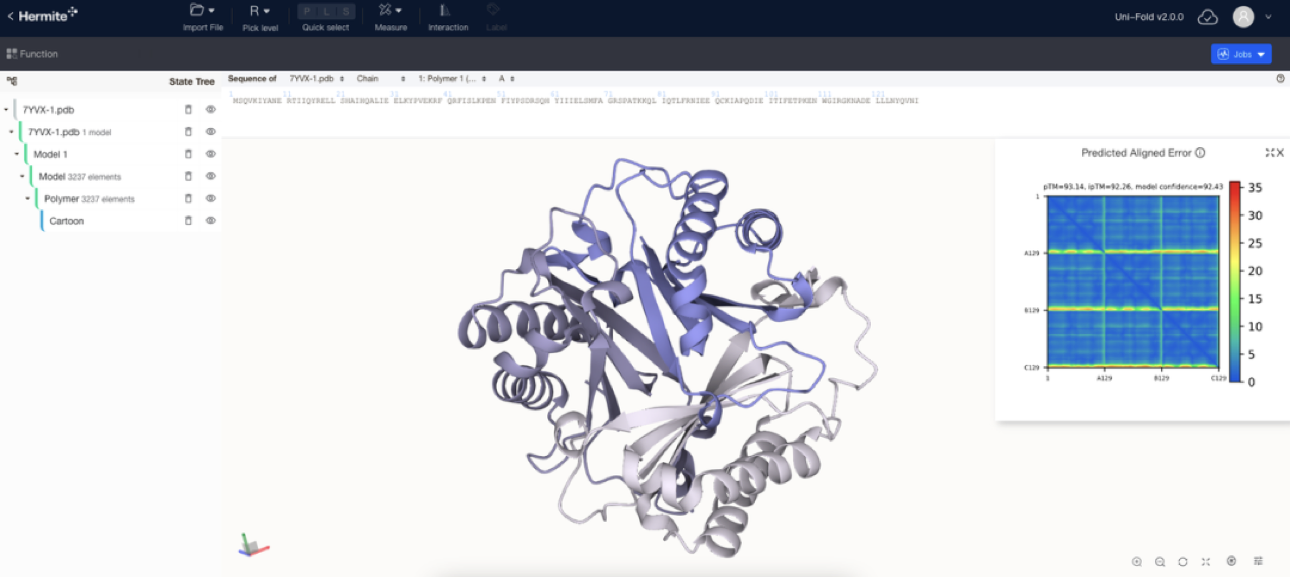
AI enterprise multi cloud storage architecture practice | Shenzhen potential technology sharing
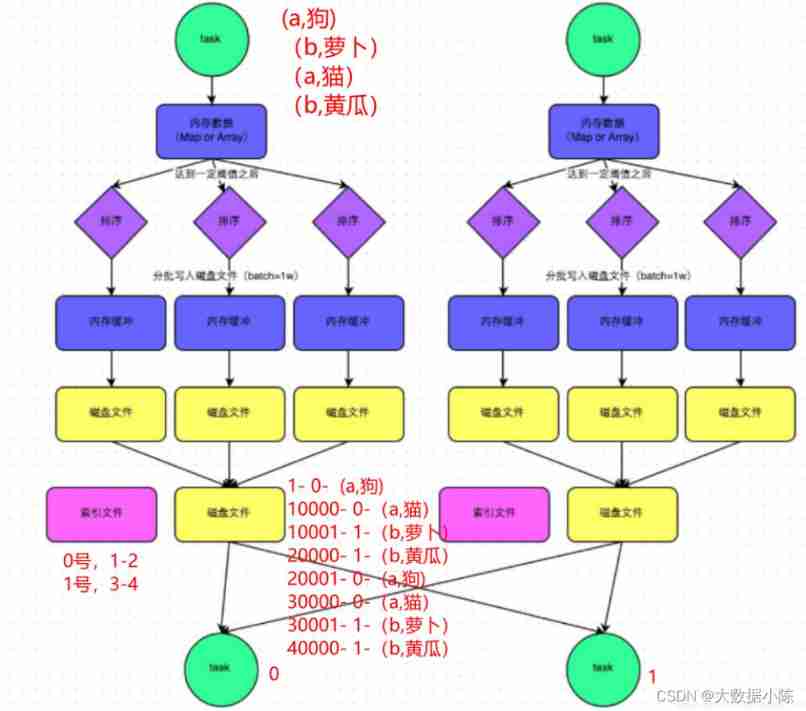
Sparkshuffle process and Mr shuffle process
PostgreSQL install GIS plug-in create extension PostGIS_ topology
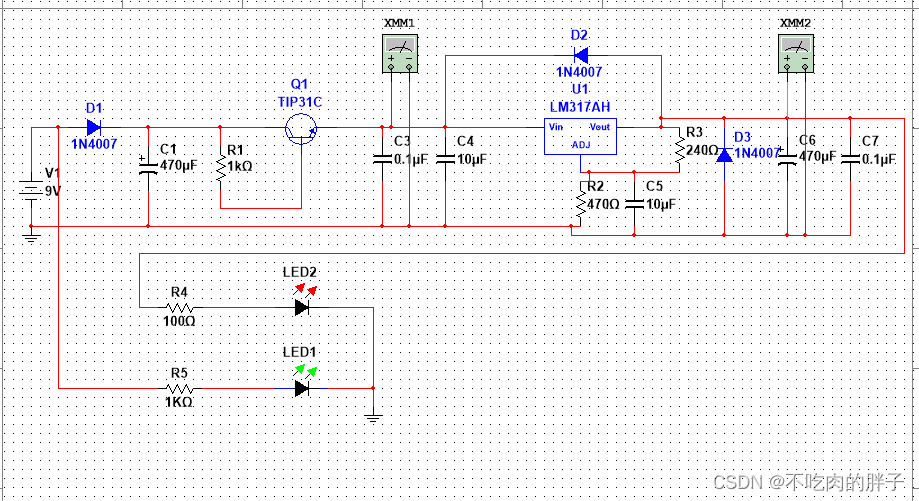
Adjustable DC power supply based on LM317

GPS从入门到放弃(十二)、 多普勒定速
Wechat red envelope cover applet source code - background independent version - source code with evaluation points function
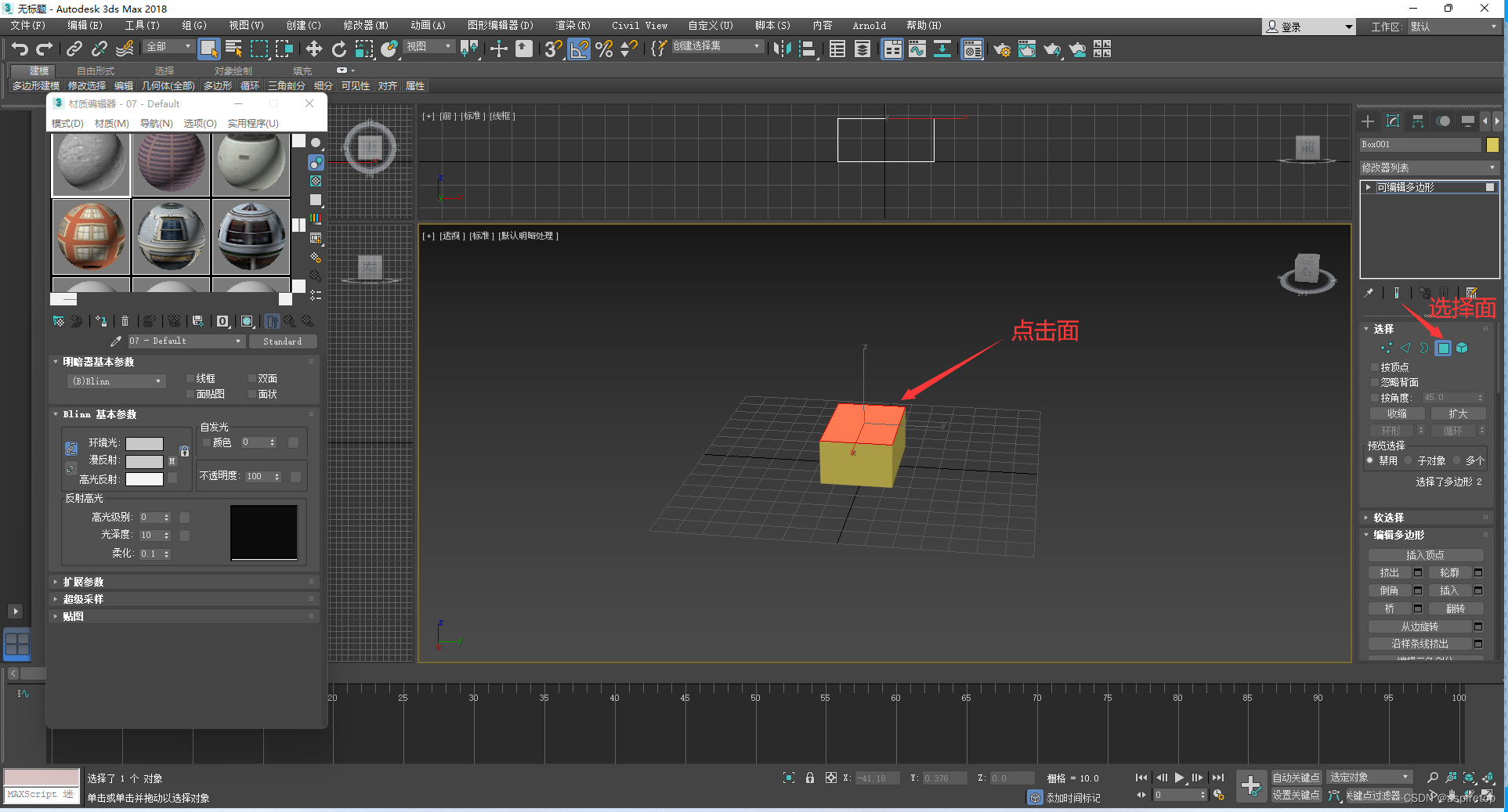
3DMax指定面贴图
随机推荐
Vit paper details
MongoDB(三)——CRUD
Mongodb (III) - CRUD
Force deduction question 500, keyboard line, JS implementation
11、 Service introduction and port
HDR image reconstruction from a single exposure using deep CNNs阅读札记
Univariate cubic equation - relationship between root and coefficient
华为在多个行业同时出击,吓人的技术让欧美企业瑟瑟发抖
GPS从入门到放弃(十九)、精密星历(sp3格式)
PostgreSQL modifies the password of the database user
美国科技行业结束黄金时代,芯片求售、裁员3万等哀声不断
AI 企业多云存储架构实践 | 深势科技分享
功能强大的国产Api管理工具
NPM run dev start project error document is not defined
Bat script learning (I)
MariaDB database management system learning (I) installation diagram
Shell product written examination related
Digital transformation takes the lead to resume production and work, and online and offline full integration rebuilds business logic
Why is the cluster mode of spark on Yan better than the client mode
微信红包封面小程序源码-后台独立版-带测评积分功能源码