Explanation of bitwise operators

Catalog

                                                 And （&）

                                                or （|）

                                                Not （~）

                                                Exclusive or （^）

                                                 Shift Operators

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        1.>> Move right  

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​ 2.<< Move left

---

Recently, I came into contact with bitwise operators , I think the use of bitwise operators in some problems is very clever , And it is also an introductory Algorithm .

Bit operators have , And , or , Not , Exclusive or , Shift Operators

Bit operators are actually binary operations ,

                                                And （&）

              The corresponding bits of two binary operands are the same 1 The result is Only then 1, The rest is 0;

   10 Hexadecimal number         15            Binary system     00001111

                          14                          00001110

15&14=  14（00001110）

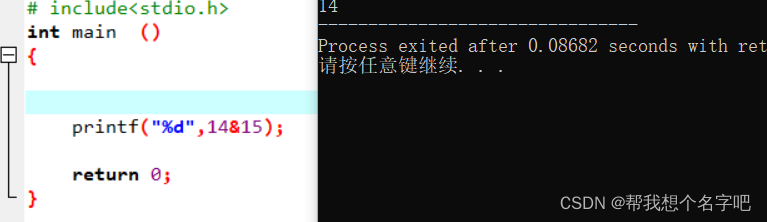
# include <stdio.h>
int main()
{
	printf("%d",14&15);
	return 0;
 } 

                                                or （|）

                  Only one of the corresponding bits of two binary operands is 1 The result is for 1, The rest is 0

 10 Hexadecimal number         15            Binary system     00001111

                        14                           00001110

15|14=15（00001111）

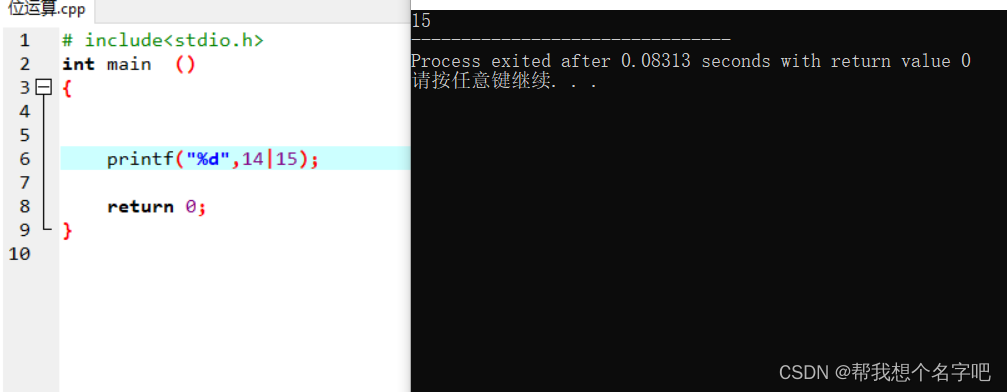
# include <stdio.h>
int main()
{
	printf("%d",14|15);
	return 0;
 } 

                                          Not （~）

              A binary operand , The corresponding bit is 0, The result bit is 1; The corresponding bit is 1, The result bit is 0;

The reverse result is the original code     When storing, it is the complement of storage , To get the complement, you need to get the inverse code first

 10 Hexadecimal number        8            Binary system     0000 1000

      （~8）=-9（1000 1001）

    Reverse the original code ：1111 0111

    Reverse code after reverse ：1000 1000（ Except for sign bits The other bits are inverted ）

    Complement after inversion ：1000 1001   Complement code （ Because it is negative, add one ） If it is a positive number, you don't need to add one  

             

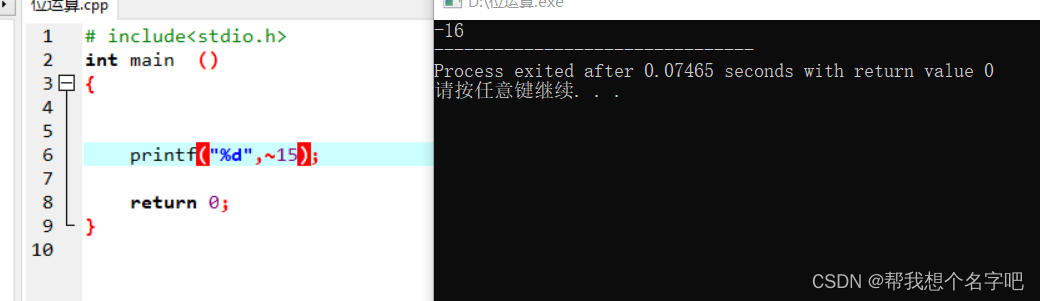
# include <stdio.h>
int main()
{
	printf("%d",~15);
	return 0;
	//00001000
	//11110111       Reverse original code 
	//10001000       Take the inverse code 
	//10001001       Complement code （ Because it is negative, add one ）  
	        
 } 

                                                    Exclusive or （^）

            Both are false , Different is true

10 Hexadecimal number         15            Binary system     00001111

                        14                           00001110

15^14=1（0000001）

# include <stdio.h>
int main()
{
	printf("%d",14^15);
	return 0;

 } 

                          Shift Operators

1.>> Move right  

  Move all the numbers to the right by the corresponding shift digits in binary form , Move out low ( Abandon ), The sign of the high position , That is, positive number plus zero , Negative numbers make up 1.（ The high bit is supplemented by the sign bit ------- Positive number right shift or positive number     Negative number right shift or negative number ）

grammar ： Numbers that need to be shifted number >> The number of shifts

13>>2=3

13 Binary bit of （1101） Move two digits to the right to become 3（11）

nature （ Under integer ）： Moving right is equivalent to dividing this number by 2 The number of shifts is rounded down

13/（2^2） Round down to 3

2.<< Move left

Shift the binary of a number to the left at the same time , In the low position 0 Add

5<<1=10

5(101) To the right 1 position （1010）=10、

The nature is the same as above, shift right

yes 5*2^1=10