当前位置：网站首页>PolarFormer: Multi-camera 3D Object Detection with Polar Transformers 论文笔记

PolarFormer: Multi-camera 3D Object Detection with Polar Transformers 论文笔记

2022-08-03 12:15:00 【byzy】

原文链接：https://arxiv.org/pdf/2206.15398.pdf

1 引言

基于多视图的图像3D目标检测很困难。为了得到3D表达，通常会使用密集深度估计，但该方法计算昂贵且容易出错。有方法使用基于查询的2D检测来绕过深度估计，在垂直轴的笛卡尔坐标系中学习一组虚拟嵌入，用于多视图图像3D目标检测。

本文认为在极坐标下表达物体更合适和自然。提出Polar Transformer（PolarFormer），在极坐标系下检测物体。首先使用序列到序列的交叉注意力学习相应于图像区域的极射线表达。然后使用在360°范围内均匀分布的极射线将极坐标BEV网格化。为处理不规则的极网格，提出基于交叉注意力的解码器，而不限制输入形状。为处理极距变化带来的物体尺度变化，提出多尺度极BEV表达学习方法。

3 方法

PolarFormer的目标是从多视图图像学习有效的极BEV表达，以在极坐标内促进预测物体参数。

如下图所示，PolarFormer由跨平面编码器、极对齐模块、极BEV编码器和极检测头组成。

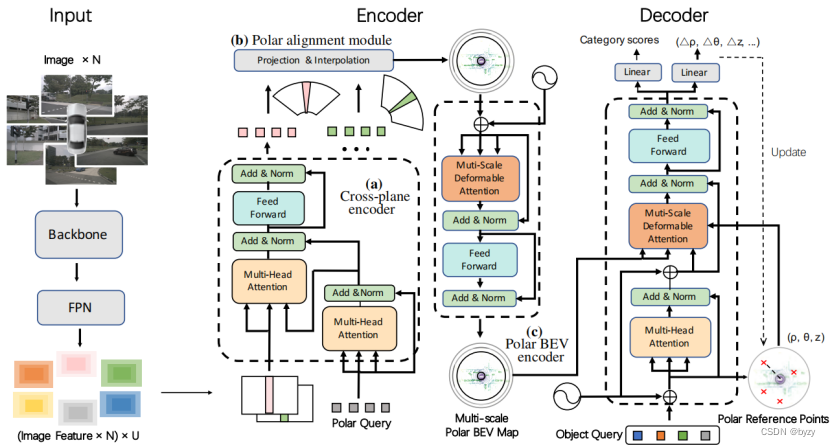
跨平面编码器使用跨平面注意力机制为每个图像生成多尺度特征表达，其中极查询从输入图像中生成BEV的3D特征。

极对齐模块从多个相机视图聚合极射线，生成结构化的极坐标图。

极BEV编码器使用多尺度特征交互加强极特征。

极检测头解码极坐标图，在极坐标系下预测物体。

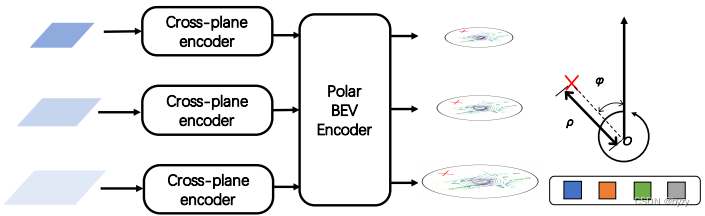
此外，为处理物体尺度变化，提出多尺度极BEV表达结构（如上图所示）。多尺度图像特征首先使用各自的跨平面编码器，然后使用公共的极BEV编码器进行交互。最后这些多尺度极BEV特征图被极BEV解码器查询。

3.1 跨平面编码器

目标是将图像和极射线关联。

图像坐标和摄像机坐标（3D空间坐标）之间的关系为：

$s\begin{bmatrix} x^{(I)}\\ y^{(I)}\\ 1 \end{bmatrix}=\begin{bmatrix} f_x & 0 & u_0\\ 0 & f_y & v_0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x^{(C)}\\ y^{(C)}\\ z^{(C)} \end{bmatrix}$

其中 f_x,f_y,u_0,v_0 属于相机内参，是缩放因子， $x^{(C)},y^{(C)},z^{(C)}$ 分别为水平坐标、垂直坐标和深度坐标。故图像坐标和极坐标之间的关系为

$\phi^{(P)}=\arctan\frac{x^{(I)}-u_0}{f_x},\rho^{(P)}=\sqrt{(x^{(C)})^2+(z^{(C)})^2}=z^{(C)}\sqrt{\left ( \frac{x^{(I)}-u_0}{f_x} \right )^2+1}$

上面第一式说明水平角 $\phi^{(P)}$ 与图像竖直位置无关，故可建立极射线与图像列的一一对应。

但由于距离 $\rho^{(P)}$ 与深度 $z^{(C)}$ 相关，不易计算。本文使用注意力机制隐式地建模图像某列像素与沿极射线位置之间的关系。

设 $f_{n,u,w}\in\mathbb{R}^{H_u\times C}$ 为第个相机、第个尺度特征图的第列（第一张图中（a）虚线框下部矩形的有色区域）， $\dot{p}_{n,u,w}\in\mathbb{R}^{R_u\times C}$ 为相应的极射线查询，其中为特征图的高度，为极坐标图的范围。则跨平面注意力为：

$p_{n,u,w}=\textup{MultiHead}(\dot{p}_{n,u,w},f_{n,u,w},f_{n,u,w})=\textup{Concat}(\textup{head}_1,\cdots,\textup{head}_h)W_u^O$

其中 $\textup{head}_i=\textup{Attention}(\dot{p}_{n,u,w}W^Q_{i,u},f_{n,u,w}W^K_{i,u},f_{n,u,w}W^V_{i,u})$ ， $W^Q_{i,u}\in \mathbb{R}^{d_{model}\times d_q}, W^K_{i,u}\in \mathbb{R}^{d_{model}\times d_k}, W^V_{i,u}\in \mathbb{R}^{d_{model}\times d_v},W^O_{u}\in \mathbb{R}^{hd_{model}\times d_k}$ ，且 $d_q=d_k=d_v=d_{model}/h$ ；是特征维度，是注意力头的数量。

将极射线特征 $p_{n,u,w}\in\mathbb{R}^{R_u\times C}$ （第一张图中（a）虚线框上部扇环形的有色区域）沿水平角维度堆叠，得到极特征图（极BEV表达/图中扇环形）：

$P_{n,u}=\textup{Stack}([p_{n,u,1},\cdots,p_{n,u,W_u}],\textup{dim}=1)\in\mathbb{R}^{R_u\times W_u\times C}$

这种基于序列到序列的交叉注意力编码器可以编码几何成像先验，隐式地学习深度。

3.2 跨相机极对齐

该模块将极射线坐标从各个相机转化到公共坐标（简单来说就是将图中的各个扇环拼接称为圆环）。

首先在柱坐标系下生成均匀的3D点 $G^{(P)}=\{(\rho_i,\phi_j,z_k)|i=1,\cdots,R_u;j=1,\cdots,N_u,k=1,\cdots,Z_u\}$ ，然后将它们投影到第个图像平面检索极射线：

$\begin{bmatrix} sx^{(I)}_{i,j,k,n}\\ sy^{(I)}_{i,j,k,n}\\ s\\ 1 \end{bmatrix}=\begin{bmatrix} \Pi_n & 0\\ 0 & 1 \end{bmatrix}E_n\begin{bmatrix} \rho_i^{(P)}\sin\phi_j^{(P)}\\ \rho_i^{(P)}\cos\phi_j^{(P)}\\ z_k^{(P)}\\ 1 \end{bmatrix}$

其中 $\Pi$ 为内参矩阵，为外参矩阵。然后第个尺度的极BEV图（第一张图中（c）虚线框上部环形区域）可按下式生成：

$G_u(\rho_i^{(P)},\phi_j^{(P)})=\frac{\sum_{n=1}^N\sum_{k=1}^Z\lambda_n(\rho_i^{(P)},\phi_j^{(P)},z_k^{(P)})B(P_{n,u},(\bar{x}^{(I)}_{i,j,k,n},\bar{r}_{i,j,n}))}{\sum_{n=1}^N\sum_{k=1}^Z\lambda_n(\rho_i^{(P)},\phi_j^{(P)},z_k^{(P)})}$

其中 $\lambda_n(\rho_i^{(P)},\phi_j^{(P)},z_k^{(P)})$ 为二值权重系数，表明点在第个图像中的可视性。 B(P,(x,r)) 表示在的 (x,r) 处进行双线性采样。 $\bar{x}^{(I)}_{i,j,k,n}$ 和 $\bar{r}_{i,j,n}$ 分别表示归一化的极射线索引和半径索引。

该模块通过生成沿平行轴分布的点来整合不同高度的特征。

3.3 极BEV多尺度编码

若 $\hat{x}_q\in[0,1]^2$ 是每个查询元素的参考点归一化坐标，则多尺度可变形注意力模块如下：

$\small \textup{MSDeformAttn}(z_q,x_q,\{G_u\}_{u=1}^U)=\sum_{m=1}^MW_m[\sum_{u=1}^U\sum_{k=1}^KA_{muqk}{W}'_mG_u(\zeta_u(\hat{x}_q)+\Delta x_{muqk})]$

其中 z_q 为查询的特征， $\Delta x_{muqk}$ 和 $A_{muqk}$ 分别为查询在第个采样点、第个特征级别、第个注意力头的采样偏移量和注意力权重，且 $A_{muqk}$ 被归一化为

$\sum_{u=1}^U\sum_{k=1}^KA_{muqk}=1$

函数 $\zeta_u$ 生成采样偏移量并放缩 $\hat{x}_q$ 到第个特征尺度。 W_m 和 ${W}'_m$ 是可学习参数。

多尺度特征图的每个像素均利用了邻域像素和其余尺度像素的信息，从而学习到更丰富的语义。

3.4 多尺度极BEV解码器

该模块解码多尺度极特征，并在极坐标下作预测。使用可变形注意力来建立解码器，将3.3节公式中的查询作为可学习参数。

解码层中的分类分支输出置信度分数向量 $c\in \mathbb{R}^O$ ，其中为类别数。回归分支的预测目标为极坐标表示。解码器迭代地细化柱坐标系下的参考点 $(\rho,\phi,z)$ ，回归偏移量 $d_\rho,d_\phi,d_z$ 。朝向角和速度与物体水平角相关，被分解为正交分量 $\theta_{\phi},\theta_{\rho},v_{\phi},v_{\rho}$ ：