当前位置:网站首页>LeetCode brush questions (8)
LeetCode brush questions (8)
2022-08-05 11:28:00 【ha_lee】
Bit operation related problems
位运算是算法题里比较特殊的一种类型,它们利用二进制位运算的特性进行一些奇妙的优化
和计算.常用的位运算符号包括:“^”按位异或、“&”按位与、“|”按位或、“~”取反、“<<”
算术左移和“>>”算术右移.以下是一些常见的位运算特性,其中0s 和1s 分别表示只由0 或1
构成的二进制数字.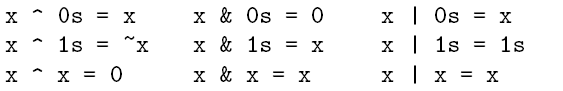
另外还有:
n & (n - 1) 可以直接将n二进制表示的最低位 1移除,例如对于二进制表示11110100,减去1 得到11110011,这两个数按位与得到11110000.
n & (-n) 可以直接获取 nn二进制表示的最低位的 1,例如对于二进制表示11110100,Invert and add one to get00001100,这两个数按位与得到00000100.
461. Hamming Distance (Easy)
问题描述
两个整数之间的 Hamming distance refers to the number of positions where the two numbers correspond to different binary digits.
给你两个整数 x 和 y,计算并返回它们之间的汉明距离.
输入输出样例
示例 1:
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
示例 2:
输入:x = 3, y = 1
输出:1
思路
XOR of two numbers,Then all the distinct digits are 1,Then count all of them1.
代码
class Solution {
public int hammingDistance(int x, int y) {
int diff = x^y; //求异或
int count = 0;
while (diff>0){
count += diff&1; //Least bit if 1则count++;
diff = diff>>1; //向右移动一位
}
return count;
}
}
190. Reverse Bits (Easy)
问题描述
颠倒给定的 32 位无符号整数的二进制位.
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型.在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的.
在 Java 中,编译器使用二进制补码记法来表示有符号整数.因此,在 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825.
输入输出样例
示例 1:
输入:n = 00000010100101000001111010011100
输出:964176192 (00111001011110000010100101000000)
解释:输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000.
示例 2:
输入:n = 11111111111111111111111111111101
输出:3221225471 (10111111111111111111111111111111)
解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 .
思路
will enter binaryn每次向右移动一位,The saved result is shifted to the left one bit at a time.当输入n移动到0时,循环结束.
代码
public class Solution {
// you need treat n as an unsigned value
public int reverseBits(int n) {
int result=0;
for(int i=0;i<32;i++){
result = result << 1; //Move to the left one bit at a time,It is equivalent to making a place
result += n&1; //将nThe last digit is added to the result,n&1结果为nlast bit of binary
n = n>>1; //n向右移动,The loop ends when the move is complete
}
return result;
}
}
136. Single Number (Easy)
问题描述
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次.找出那个只出现了一次的元素.
说明:
你的算法应该具有线性时间复杂度. 你可以不使用额外空间来实现吗?
输入输出样例
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
思路
可以利用 x^x=0 和 0^x=x的性质,XOR all numbers,Then the last value returned is the only single value.
代码
class Solution {
public int singleNumber(int[] nums) {
int s = 0;
for(int a:nums){
s^=a;
}
return s;
}
}
342. Power of Two (Easy)
问题描述
给你一个整数 n,请你判断该整数是否是 2 的幂次方.如果是,返回 true ;否则,返回 false .
如果存在一个整数 x 使得 n == 2x ,则认为 n 是 2 的幂次方.
输入输出样例
示例 1:
输入:n = 1
输出:true
解释:20 = 1
示例 2:
输入:n = 16
输出:true
解释:24 = 16
思路
如果是2的整数次幂,则满足n&(n-1)==0:由于2The integer power of binary has only one1,所以n去掉最低位的1后只剩0
也可以是 n&(-n)==n:最低位的1The representation is this2What is the integer power of .
class Solution {
public boolean isPowerOfTwo(int n) {
// return (n>0) && (n&(-n))==n;
return (n>0) && (n&(n-1))==0;
}
}
342. Power of Four (Easy)
问题描述
给定一个整数,写一个函数来判断它是否是 4 的幂次方.如果是,返回 true ;否则,返回 false .
整数 n 是 4 的幂次方需满足:存在整数 x 使得 n == 4x
输入输出样例
示例 1:
输入:n = 16
输出:true
示例 2:
输入:n = 5
输出:false
思路
判断是4的整数次幂,首先要是2的整数次幂.其次,in its binary representation1Occurs in odd-numbered positions.So we can judge yes2on the basis of integer powers,加上判断1whether it appears in odd-numbered digits.
A method to determine whether an odd-numbered bit is present:构造一个32位的二进制表示(10101010101010101010101010101010),Use the sum operation of this number with the input value,如果为0It indicates the number of bits in the binary representation of the input number1出现在奇数位上.This binary can be more conveniently represented in hexadecimal:oxaaaaaaaa
代码
class Solution {
public boolean isPowerOfFour(int n) {
return n>0 && (n&(-n))==n && (n&(0xaaaaaaaa))==0;
}
}
318. Maximum Product of Word Lengths (Medium)
问题描述
给你一个字符串数组 words ,找出并返回 length(words[i]) * length(words[j]) 的最大值,并且这两个单词不含有公共字母.如果不存在这样的两个单词,返回 0 .
输入输出样例
示例 1:
输入:words = [“abcw”,“baz”,“foo”,“bar”,“xtfn”,“abcdef”]
输出:16
解释:这两个单词为 “abcw”, “xtfn”.
示例 2:
输入:words = [“a”,“ab”,“abc”,“d”,“cd”,“bcd”,“abcd”]
输出:4
解释:这两个单词为 “ab”, “cd”.
思路
The general idea of this problem is to use two layers of traversal,Finds the product of the lengths of two strings that do not contain common letters.The general idea is to judge whether it contains common letters,It may be possible to loop over the two strings again to compare,The time complexity will be high.If you open up a letter hash table to store the number of occurrences of each character,空间复杂度就会很高.
The solution here is to solve whether two letters contain the same character:创建一个26位二进制数,某位为1The letter representing that position exists in the current string.After that, just use the binary numbers in the corresponding positions of the two strings to perform the sum operation,为0It means that the two strings have no common letters.
代码
class Solution {
public int maxProduct(String[] words) {
List<Integer> list = new ArrayList<Integer>();
for(String word:words){
int a = 0;
for(char w:word.toCharArray()){
a |= 1<<w-'a'; //1<<w-'a'表示将1Move the corresponding number of digits to the left,Then use and operate to add to26位二进制数中(不能使用+,会产生进位)
}
list.add(a);
}
int n = words.length;
int max = 0;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(j!=i && (list.get(i)&list.get(j))==0){
max = Math.max(max,words[i].length()*words[j].length());
}
}
}
return max;
}
}
338. Counting Bits (Medium)
问题描述
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算in its binary representation 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案.
输入输出样例
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
思路
常规思路:对于0-n中的每一个数,看最低位是否为1,是则计数,Then shift right by one bit until each number is counted.
使用动态规划:
对于所有的数字,只有两类:
奇数:二进制表示中,奇数一定比前面那个偶数多一个 1,因为多的就是最低位的 1.dp[i]=dp[i-1]+1;
举例:
0 = 0 1 = 1
2 = 10 3 = 11
偶数:二进制表示中,偶数中 1 的个数一定和除以 2 之后的那The same number.因为最低位是 0,除以 2 就是右移一位,也就是把那个 0 抹掉而已,所以 1 的个数是不变的.dp[i]=dp[i/2];可以理解为:对于偶数j,Its lowest bit is 0,它包含的1and the number shifted to the right by one1The same number.
举例:
2 = 10 4 = 100 8 = 1000
3 = 11 6 = 110 12 = 1100
代码(思路1)
class Solution {
public int[] countBits(int n) {
int[] result = new int[n+1];
for(int i=0;i<=n;i++){
int current = i;
int count = 0;
while (current>0){
if((current&1) == 1){
count++;
}
current = current>>1;
}
result[i]=count;
}
return result;
}
}
代码(思路二)
class Solution {
public int[] countBits(int n) {
int[] dp = new int[n+1];
for(int i=0;i<=n;i++){
if((i&1)==0){
//以0结尾
dp[i]=dp[i>>1];
}else dp[i]=dp[i-1]+1;
}
return dp;
}
}
268. Missing Number (Easy)
问题描述
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数.
输入输出样例
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内.2 是丢失的数字,因为它没有出现在 nums 中.
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内.2 是丢失的数字,因为它没有出现在 nums 中.
思路
思路1:利用数学方法,使用1~nThe sum of the numbers minus the sum of the arrays,is the missing number.
思路2:Use a hash array to store the number of occurrences of a number,Then iterate over the hash array,如果某个元素为0It means that the number of this position is default.
思路3:Use bit correlation operations.将1~nXOR the numbers in the array with the numbers in the array,由于X^X=0 ;0^x=x
代码(思路1)
class Solution {
public int missingNumber(int[] nums) {
int sum = 0;
int n = nums.length;
for(int a:nums)sum+=a;
int n_sum = n*(n+1)/2;
return n_sum-sum;
}
}
代码(思路2)
class Solution {
public int missingNumber(int[] nums) {
int n = nums.length;
int[]count = new int[n+1];
for(int i=0;i<n;i++){
count[nums[i]]++;
}
for(int i=0;i<=n;i++){
if(count[i]==0)return i;
}
return -1;
}
}
代码(思路3)
class Solution {
public int missingNumber(int[] nums) {
int sum =0;
for(int a:nums){
sum ^= a;
}
for(int i=0;i<=nums.length;i++){
sum ^= i;
}
return sum;
}
}
693. Binary Number with Alternating Bits (Easy)
问题描述
给定一个正整数,检查它的二进制表示是否总是 0、1 交替出现:换句话说,就是二进制表示中相邻两位的数字永不相同.
输入输出样例
示例 1:
输入:n = 5
输出:true
解释:5 的二进制表示是:101
示例 2:
输入:n = 7
输出:false
解释:7 的二进制表示是:111.
思路
如果nis a binary representation01number of intervals,n&(n>>1)==0.So the inverse negative proposition is :if(n&(n>>1)!=0返回false.
如果n&(n>>1)==0,Two need to be considered0相邻的情况,如(100)【4】,求n|(n>>1),If the result is all 1It means that they are adjacent,存在0It means there are two0相邻的情况,返回false.
代码
class Solution {
public boolean hasAlternatingBits(int n) {
if((n>>1 & n)!=0)return false; //考虑两个1相邻的情况
int a = (n>>1 | n); //考虑两个0相邻的情况
while (a>0){
if((a&1)==0)return false;
a = a>>1;
}
return true;
}
}
476. Number Complement (Easy)
问题描述
对整数的二进制表示取反(0 变 1 ,1 变 0)后,再转换为十进制表示,可以得到这个整数的补数.
例如,整数 5 的二进制表示是 “101” ,取反后得到 “010” ,再转回十进制表示得到补数 2 .
给你一个整数 num ,输出它的补数.
输入输出样例
示例 1:
输入:num = 5
输出:2
解释:5 的二进制表示为 101(没有前导零位),其补数为 010.所以你需要输出 2 .
示例 2:
输入:num = 1
输出:0
解释:1 的二进制表示为 1(没有前导零位),其补数为 0.所以你需要输出 0 .
思路
对于任意一个二进制数 100110,The way to find its inverse code is to be all of the same number of digits1The numbers are XORed.即1^x=-x
代码
class Solution {
public int findComplement(int num) {
int pre = 0;
int num1 = num;
while (num>0){
pre <<= 1;
pre += 1; //构造一个全为1的二进制数
num >>=1;
}
return pre^num1;
}
}
260. Single Number III (Medium)
问题描述
给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次. 找出只出现一次的那两个元素.你可以按 任意顺序 返回答案.
进阶:你的算法应该具有线性时间复杂度.你能否仅使用常数空间复杂度来实现?
输入输出样例
示例 1:
输入:nums = [1,2,1,3,2,5]
输出:[3,5]
解释:[5, 3] 也是有效的答案.
示例 2:
输入:nums = [-1,0]
输出:[-1,0]
思路
You can XOR all elements in an array,This is because there are two different numbers,最后的结果xis not zero and must be these two distinct numbersa和b的异或值.So the problem becomes,如何将x分解为a和b.
Because of the nature of XOR, the same is0,不同为1.我们可以找到x二进制中第i位为1的位置,Divide the array into two groups:第i的位置为1和第i的位置为0的元素.Each of these two sets of elements has only one distinct number【these two different numbersiThe number of positions must be different,通过这个方式可以把a,b分开】,Again, XOR the two groups together to find the two distinct elements.
代码
class Solution {
public int[] singleNumber(int[] nums) {
int xor = 0;
for(int num:nums)xor ^= num;
int x = xor & (-xor); //找到xor最后一个1所在的位置i
int a=0,b=0;
for(int num:nums){
if((num & x)!=0){
//i位置为1XOR the elements of
a ^= num;
}else b ^= num; //i位置为0XOR the elements of
}
return new int[]{
a,b};
}
}
边栏推荐
- JS 从零手写实现一个call、apply方法
- STM32 entry development: write XPT2046 resistive touch screen driver (analog SPI)
- lvgl 实现状态提示图标自动对齐补位显示
- 一张图看懂 SQL 的各种 join 用法!
- poj2287 Tian Ji -- The Horse Racing(2016xynu暑期集训检测 -----C题)
- 5G NR 系统消息
- EOS的共识机制与区块生成
- Http-Sumggling缓存漏洞分析
- Flink Yarn Per Job - 启动TM,向RM注册,RM分配solt
- Linux:记一次CentOS7安装MySQL8(博客合集)
猜你喜欢
DocuWare平台——文档管理的内容服务和工作流自动化的平台详细介绍(下)

《分布式云最佳实践》分论坛,8 月 11 日深圳见

Flink Yarn Per Job - 启动TM,向RM注册,RM分配solt
gradle尚硅谷笔记
【硬件架构的艺术】学习笔记(3)处理多个时钟
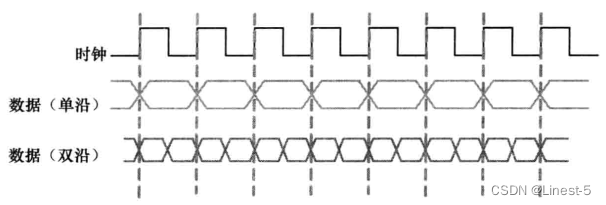
【硬件架构的艺术】学习笔记(2)同步和复位
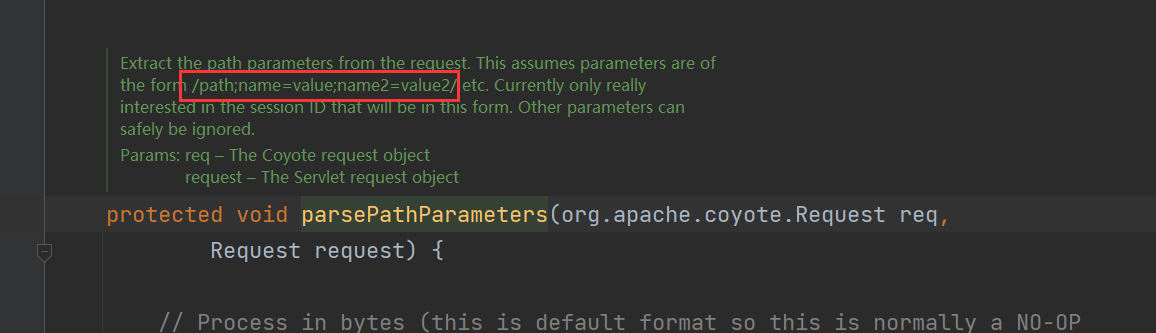
反射修改jsessionid实现Session共享
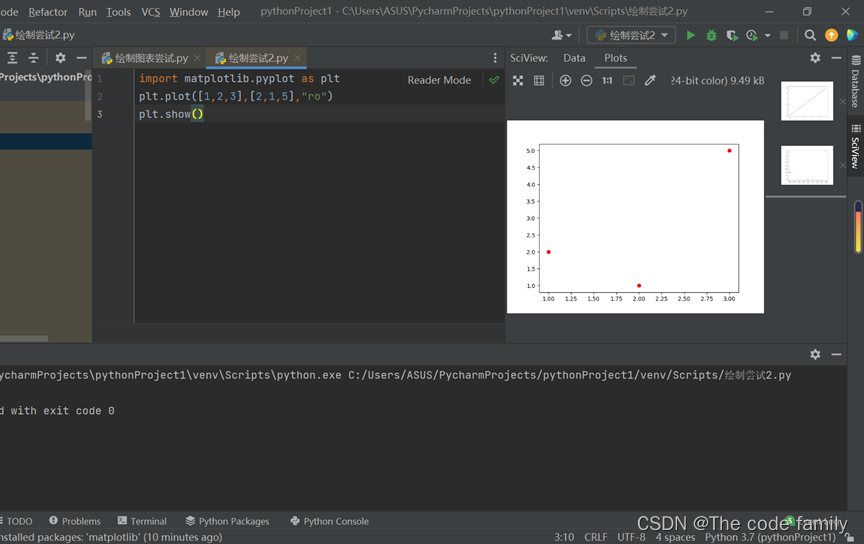
数据可视化(二)
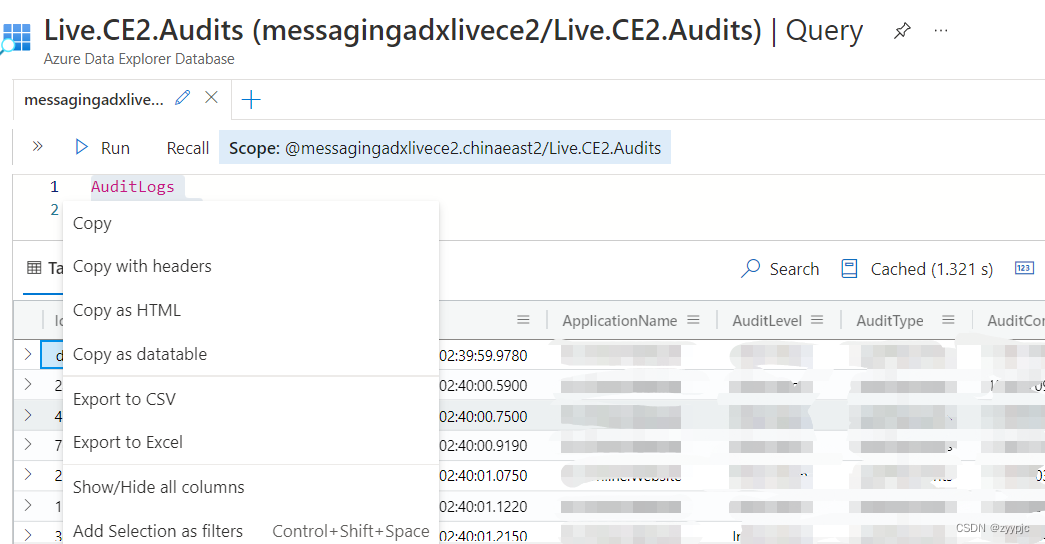
Use KUSTO query statement (KQL) to query LOG on Azure Data Explorer Database

#yyds干货盘点#【愚公系列】2022年08月 Go教学课程 001-Go语言前提简介
随机推荐
L2-042 老板的作息表
智源社区AI周刊No.92:“计算复杂度”理论奠基人Juris Hartmanis逝世;美国AI学生九年涨2倍,大学教师短缺;2022智源大会观点报告发布[附下载]
再获殊荣 | 赛宁网安入选2022年度“培育独角兽”企业榜单
UDP communication
Machine Learning - Logistic Regression
【硬件架构的艺术】学习笔记(3)处理多个时钟
Student Information Management System (first time...)
R语言ggplot2可视化:可视化密度图(Density plot)、可视化多个分组的密度图、数据点分布在箱图中间、添加主标题、副标题、题注信息
OpenHarmony如何查询设备类型
MMDetection in action: MMDetection training and testing
机器学习——逻辑回归
Guys, I am a novice. I use flinksql to write a simple count of user visits according to the document, but it ends after executing it once.
HDD杭州站•ArkUI让开发更灵活
Dynamics 365Online PDF导出及打印
#yyds干货盘点#JS数组和树相互转化
Google启动通用图像嵌入挑战赛
智能算力的枢纽如何构建?中国云都的淮海智算中心打了个样
【AGC】增长服务1-远程配置示例
【加密解密】明文加密解密-已实现【已应用】
拓朴排序例题