当前位置:网站首页>[mathematical logic] predicate logic (predicate logic basic equivalent | eliminate quantifier equivalent | quantifier negative equivalent | quantifier scope contraction expansion equivalent | quantifi
[mathematical logic] predicate logic (predicate logic basic equivalent | eliminate quantifier equivalent | quantifier negative equivalent | quantifier scope contraction expansion equivalent | quantifi
2022-07-03 03:53:00 【Programmer community】
List of articles
- One 、 Eliminate quantifiers Equivalent formula
- Two 、 Quantifier negation Equivalent formula
- 3、 ... and 、 The scope of quantifiers shrinks and expands Equivalent formula
- Four 、 Quantifier assignment Equivalent formula
One 、 Eliminate quantifiers Equivalent formula
Eliminate quantifier equivalents :
Finite individual field
D
=
{
a
1
,
a
2
,
⋯
,
a
n
}
D = \{a_1 , a_2 , \cdots , a_n\}
D={ a1,a2,⋯,an} , Eliminate quantifiers Of Equivalent formula :
Finite individual field eliminate Full name quantifier :
∀
x
A
(
x
)
⇔
A
(
a
1
)
∧
A
(
a
2
)
∧
⋯
∧
A
(
a
n
)
\forall x A(x) \Leftrightarrow A(a_1) \land A(a_2) \land \cdots \land A(a_n)
∀xA(x)⇔A(a1)∧A(a2)∧⋯∧A(an)
Finite individual field eliminate There are quantifiers :
∃
x
A
(
x
)
⇔
A
(
a
1
)
∨
A
(
a
2
)
∨
⋯
∨
A
(
a
n
)
\exist x A(x) \Leftrightarrow A(a_1) \lor A(a_2) \lor \cdots \lor A(a_n)
∃xA(x)⇔A(a1)∨A(a2)∨⋯∨A(an)
Be sure to pay attention to the premise : Finite individual field ;
When the individual domain is infinite , You need quantifiers , Such as Total individual domain ;
Two 、 Quantifier negation Equivalent formula
Negative full quantifier : Full name quantifier
∀
\forall
∀ Before Of Negative connectives , Can be moved to quantifiers after , Quantifiers should become There are quantifiers
∃
\exist
∃ ;
¬
∀
x
A
(
x
)
⇔
∃
x
¬
A
(
x
)
\lnot \forall x A(x) \Leftrightarrow \exist x \lnot A(x)
¬∀xA(x)⇔∃x¬A(x)
Equivalent interpretation :
¬
∀
x
A
(
x
)
\lnot \forall x A(x)
¬∀xA(x) : Not all
x
x
x All have properties
A
A
A ;
∃
x
¬
A
(
x
)
\exist x \lnot A(x)
∃x¬A(x) : There is
x
x
x Not of a nature
A
A
A ;
- The above two formulas are equivalent ;
Negative existential quantifiers : There are quantifiers
∃
\exist
∃ Before Of Negative connectives , Can be moved to quantifiers after , Quantifiers should become Full name quantifier
∀
\forall
∀ ;
¬
∃
x
A
(
x
)
⇔
∀
x
¬
A
(
x
)
\lnot \exist x A(x) \Leftrightarrow \forall x \lnot A(x)
¬∃xA(x)⇔∀x¬A(x)
Equivalent interpretation :
¬
∃
x
A
(
x
)
\lnot \exist x A(x)
¬∃xA(x) : non-existent
x
x
x Have the quality of
A
A
A ;
∀
x
¬
A
(
x
)
\forall x \lnot A(x)
∀x¬A(x) : be-all
x
x
x Have no nature
A
A
A ;
- The above two formulas are equivalent ;
3、 ... and 、 The scope of quantifiers shrinks and expands Equivalent formula
hypothesis
B
B
B It's the formula ,
B
B
B It does not contain
x
x
x ( Premise is very important ) ;
1. Full name quantifier The scope shrinks and expands ( Disjunctive connectives ) :
∀
x
(
A
(
x
)
∨
B
)
⇔
∀
x
A
(
x
)
∨
B
\forall x ( A(x) \lor B ) \Leftrightarrow \forall x A(x) \lor B
∀x(A(x)∨B)⇔∀xA(x)∨B
- The full quantifier on the left
∀
x
\forall x
∀x Our jurisdiction is
(
A
(
x
)
∨
B
)
( A(x) \lor B )
(A(x)∨B)
- The full quantifier on the right
∀
x
\forall x
∀x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
A
(
x
)
∨
B
)
( A(x) \lor B )
(A(x)∨B) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
A
(
x
)
∨
B
)
( A(x) \lor B )
(A(x)∨B)
2. There are quantifiers The scope shrinks and expands ( Disjunctive connectives ) :
∃
x
(
A
(
x
)
∨
B
)
⇔
∃
x
A
(
x
)
∨
B
\exist x ( A(x) \lor B ) \Leftrightarrow \exist x A(x) \lor B
∃x(A(x)∨B)⇔∃xA(x)∨B
- The existential quantifier on the left
∃
x
\exist x
∃x Our jurisdiction is
(
A
(
x
)
∨
B
)
( A(x) \lor B )
(A(x)∨B)
- The existential quantifier on the right
∃
x
\exist x
∃x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
A
(
x
)
∨
B
)
( A(x) \lor B )
(A(x)∨B) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
A
(
x
)
∨
B
)
( A(x) \lor B )
(A(x)∨B)
3. Full name quantifier The scope shrinks and expands ( Conjunctions ) :
∀
x
(
A
(
x
)
∧
B
)
⇔
∀
x
A
(
x
)
∧
B
\forall x ( A(x) \land B ) \Leftrightarrow \forall x A(x) \land B
∀x(A(x)∧B)⇔∀xA(x)∧B
- The full quantifier on the left
∀
x
\forall x
∀x Our jurisdiction is
(
A
(
x
)
∧
B
)
( A(x) \land B )
(A(x)∧B)
- The full quantifier on the right
∀
x
\forall x
∀x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
A
(
x
)
∧
B
)
( A(x) \land B )
(A(x)∧B) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
A
(
x
)
∧
B
)
( A(x) \land B )
(A(x)∧B)
4. There are quantifiers The scope shrinks and expands ( Conjunctions ) :
∃
x
(
A
(
x
)
∧
B
)
⇔
∃
x
A
(
x
)
∧
B
\exist x ( A(x) \land B ) \Leftrightarrow \exist x A(x) \land B
∃x(A(x)∧B)⇔∃xA(x)∧B
- The existential quantifier on the left
∃
x
\exist x
∃x Our jurisdiction is
(
A
(
x
)
∧
B
)
( A(x) \land B )
(A(x)∧B)
- The existential quantifier on the right
∃
x
\exist x
∃x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
A
(
x
)
∧
B
)
( A(x) \land B )
(A(x)∧B) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
A
(
x
)
∧
B
)
( A(x) \land B )
(A(x)∧B)
5. Full name quantifier The scope shrinks and expands ( Contains connectives B On the right ) :
∀
x
(
A
(
x
)
→
B
)
⇔
∃
x
A
(
x
)
→
B
\forall x ( A(x) \to B ) \Leftrightarrow \exist x A(x) \to B
∀x(A(x)→B)⇔∃xA(x)→B
- The full quantifier on the left
∀
x
\forall x
∀x Our jurisdiction is
(
A
(
x
)
→
B
)
( A(x) \to B )
(A(x)→B)
- The existential quantifier on the right
∃
x
\exist x
∃x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
A
(
x
)
→
B
)
( A(x) \to B )
(A(x)→B) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
A
(
x
)
→
B
)
( A(x) \to B )
(A(x)→B)
6. There are quantifiers The scope shrinks and expands ( Contains connectives B On the right ) :
∃
x
(
A
(
x
)
→
B
)
⇔
∀
x
A
(
x
)
→
B
\exist x ( A(x) \to B ) \Leftrightarrow \forall x A(x) \to B
∃x(A(x)→B)⇔∀xA(x)→B
- The existential quantifier on the left
∃
x
\exist x
∃x Our jurisdiction is
(
A
(
x
)
→
B
)
( A(x) \to B )
(A(x)→B)
- The full quantifier on the right
∀
x
\forall x
∀x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
A
(
x
)
→
B
)
( A(x) \to B )
(A(x)→B) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
A
(
x
)
→
B
)
( A(x) \to B )
(A(x)→B)
( Use Implication equivalence elimination Contains connectives Can prove that )
7. Full name quantifier The scope shrinks and expands ( Contains connectives B On the left ) :
∀
x
(
B
→
A
(
x
)
)
⇔
B
→
∀
x
A
(
x
)
\forall x ( B \to A(x) ) \Leftrightarrow B \to \forall x A(x)
∀x(B→A(x))⇔B→∀xA(x)
- The full quantifier on the left
∀
x
\forall x
∀x Our jurisdiction is
(
B
→
A
(
x
)
)
( B \to A(x) )
(B→A(x))
- The full quantifier on the right
∀
x
\forall x
∀x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
B
→
A
(
x
)
)
( B \to A(x) )
(B→A(x)) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
B
→
A
(
x
)
)
( B \to A(x) )
(B→A(x))
8. There are quantifiers The scope shrinks and expands ( Contains connectives B On the left ) :
∃
x
(
B
→
A
(
x
)
)
⇔
B
→
∃
x
A
(
x
)
\exist x ( B \to A(x) ) \Leftrightarrow B \to \exist x A(x)
∃x(B→A(x))⇔B→∃xA(x)
- The existential quantifier on the left
∃
x
\exist x
∃x Our jurisdiction is
(
B
→
A
(
x
)
)
( B \to A(x) )
(B→A(x))
- The existential quantifier on the right
∃
x
\exist x
∃x Our jurisdiction is
A
(
x
)
A(x)
A(x)
- From left to right : Jurisdiction by
(
B
→
A
(
x
)
)
( B \to A(x) )
(B→A(x)) Shrink to
A
(
x
)
A(x)
A(x)
- From right to left : Jurisdiction by
A
(
x
)
A(x)
A(x) Expand into
(
B
→
A
(
x
)
)
( B \to A(x) )
(B→A(x))
Four 、 Quantifier assignment Equivalent formula
1. Full name quantifier about Syntaxis
∧
\land
∧ Distribution rate :
∀
x
(
A
(
x
)
∧
B
(
x
)
)
⇔
∀
x
A
(
x
)
∧
∀
x
B
(
x
)
\forall x ( A(x) \land B(x) ) \Leftrightarrow \forall x A(x) \land \forall x B(x)
∀x(A(x)∧B(x))⇔∀xA(x)∧∀xB(x)
understand : All objects have
A
,
B
A , B
A,B Two properties , Equivalent to All objects have
A
A
A nature and All objects have
B
B
B nature ;
Save all weighing words about Conjunctions
∧
\land
∧ There is a distribution rate , about Disjunctive connectives
∨
\lor
∨ Not suitable for distribution rate ;
2. There are quantifiers about Disjunction
∨
\lor
∨ Distribution rate :
∃
x
(
A
(
x
)
∨
B
(
x
)
)
⇔
∃
x
A
(
x
)
∨
∃
x
B
(
x
)
\exist x ( A(x) \lor B(x) ) \Leftrightarrow \exist x A(x) \lor \exist x B(x)
∃x(A(x)∨B(x))⇔∃xA(x)∨∃xB(x)
understand : Objects exist Or there is
A
A
A nature , Or there is
B
B
B nature ;
There are quantifiers about Disjunctive connectives
∨
\lor
∨ There is a distribution rate , about Conjunctions
∧
\land
∧ Not suitable for distribution rate ;
边栏推荐
- Role of JS No
- Recursion: one dimensional linked lists and arrays
- Advanced redis applications [password protection, data persistence, master-slave synchronization, sentinel mode, transactions] [not completed yet (semi-finished products)]
- 2022 P cylinder filling examination content and P cylinder filling practice examination video
- Introduction to mongodb
- Makefile demo
- [Blue Bridge Road - bug free code] pcf8591 - code analysis of AD conversion
- TCP, the heavyweight guest in tcp/ip model -- Kuige of Shangwen network
- Dynamic programming: Longest palindrome substring and subsequence
- Bid farewell to artificial mental retardation: Mengzi open source project team received RMB 100 million financing to help NLP develop
猜你喜欢

2022 mobile crane driver examination registration and mobile crane driver operation examination question bank
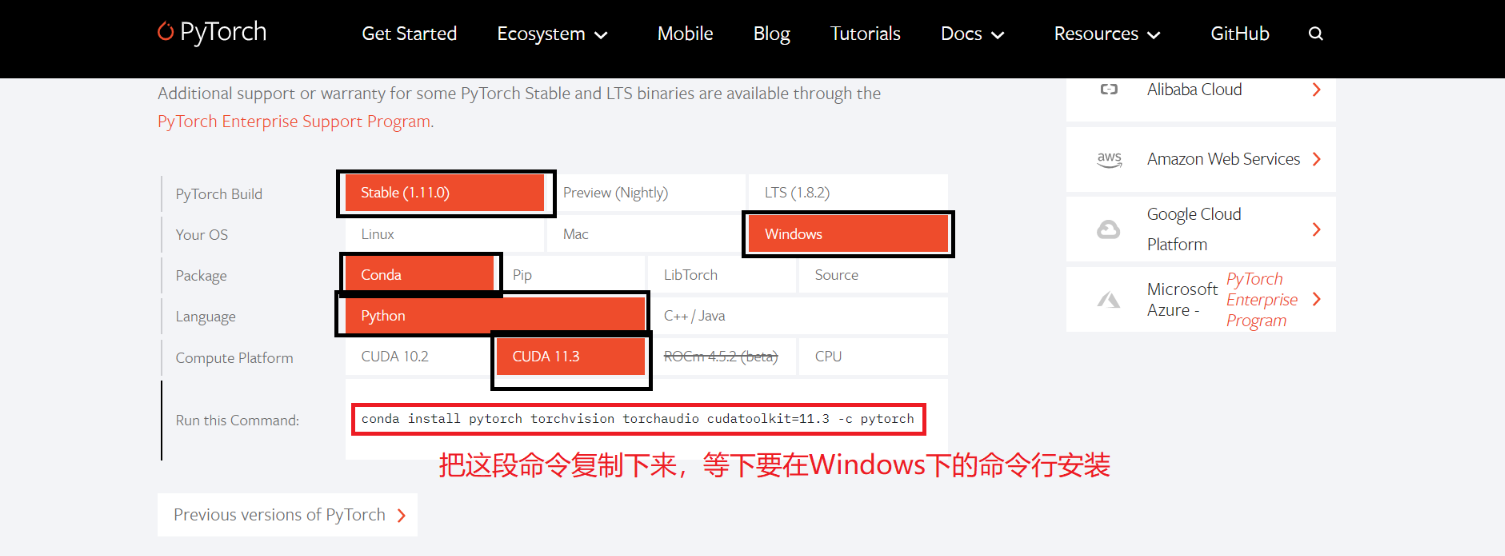
pytorch怎么下载?pytorch在哪里下载?

Is pytorch open source?
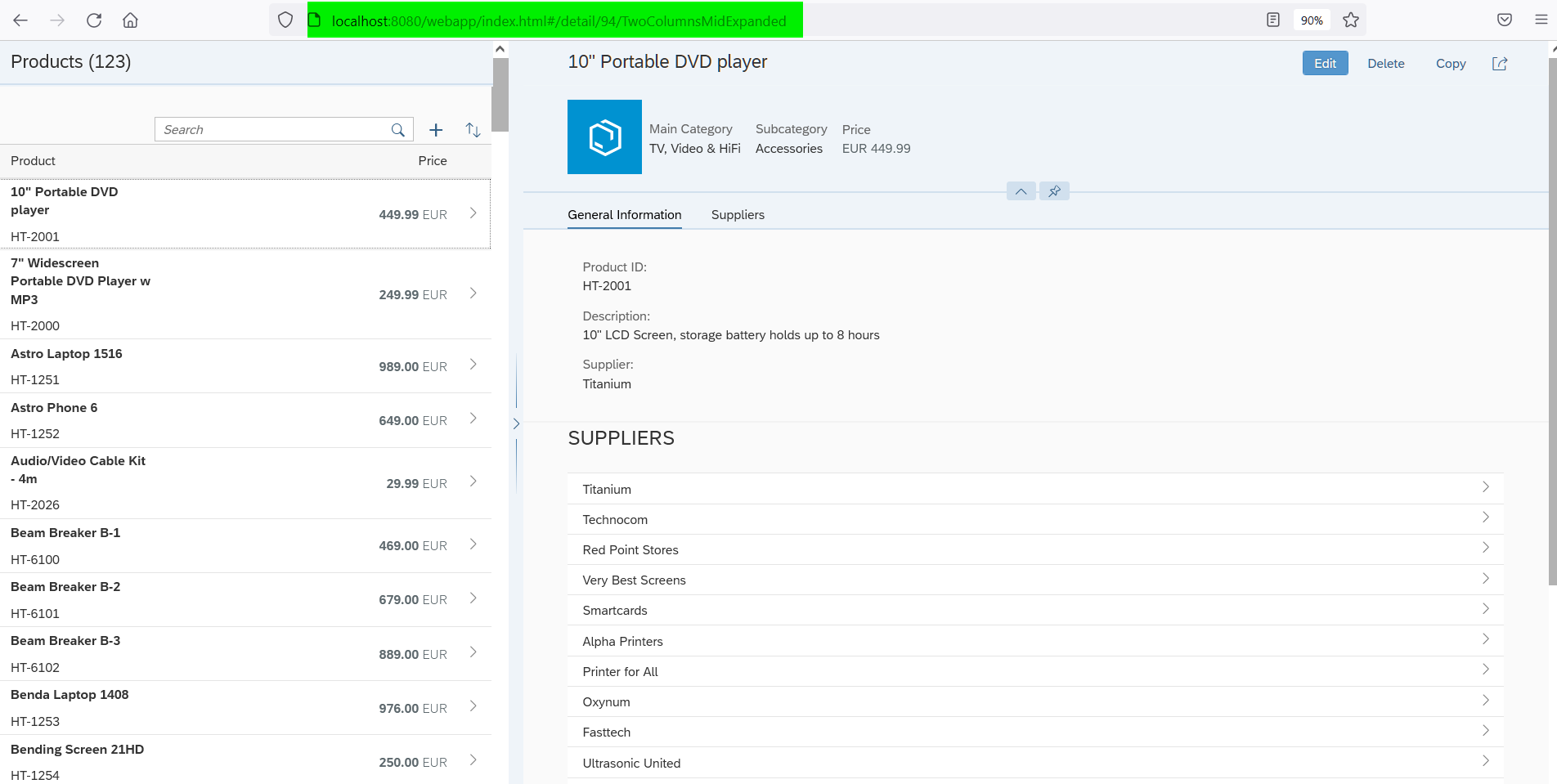
105. Detailed introduction of linkage effect realization of SAP ui5 master detail layout mode

Wechat applet + Alibaba IOT platform + Hezhou air724ug build a serverless IOT system (III) -- wechat applet is directly connected to Alibaba IOT platform aliiot

Cnopendata China Customs Statistics

中移物联网OneOS与OneNET入选《2021年物联网示范项目名单》
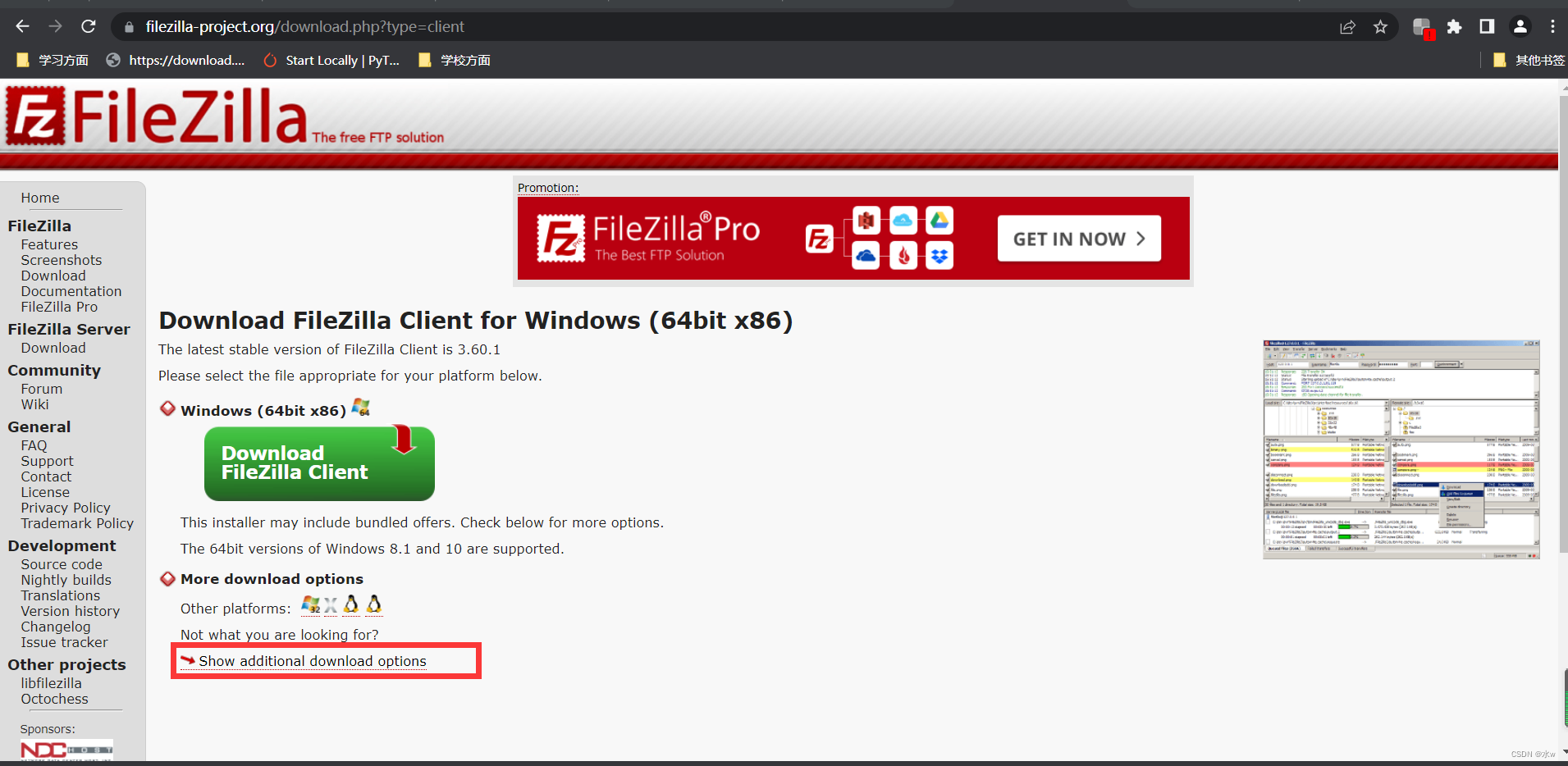
Téléchargement et installation du client Filezilla

Captura下载安装及在Captura配置FFmpeg

docker安装及启动mysql服务
随机推荐
第十届中国云计算大会·中国站:展望未来十年科技走向
ffmpeg下载安装教程及介绍
2022 Shandong Province safety officer C certificate examination questions and Shandong Province safety officer C certificate simulation examination question bank
ffmpeg之 一张/多张图片合成视频
『期末复习』16/32位微处理器(8086)基本寄存器
Simple wechat applet development page Jump, data binding, obtaining user information, obtaining user location information
105. SAP UI5 Master-Detail 布局模式的联动效果实现明细介绍
Filter
shardingsphere动态数据源
js中#号的作用
【DRM】DRM bridge驱动调用流程简单分析
Read a paper_ ChineseBert
Wechat applet + Alibaba IOT platform + Hezhou air724ug build a serverless IOT system (III) -- wechat applet is directly connected to Alibaba IOT platform aliiot
2022-07-02:以下go语言代码输出什么?A:编译错误;B:Panic;C:NaN。 package main import “fmt“ func main() { var a =
2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video
Mongodb installation & Deployment
Separable bonds and convertible bonds
TCP/IP模型中的重磅嘉宾TCP--尚文网络奎哥
node,npm以及yarn下载安装
TCP, the heavyweight guest in tcp/ip model -- Kuige of Shangwen network