Recursion: one dimensional linked lists and arrays

Reverse string

Write a function , Its function is to invert the input string . Input string as character array s Given in the form of .
Recursion is to transform a big problem into the same small problem , The original problem is the same as the minor problem , But the scale of the problem has been reduced . When reversing the string , In fact, it is the exchange of characters at both ends , Then go to the middle one by one .

l —>				<— r
h	e	l	l	o
	l —>	l	<— r
o	e	l	l	h

You can see , Repeat the operation to exchange the strings on the left and right sides , Then the string keeps shrinking （ The scale of the problem has shrunk ）, But the operation is always repeated .

When reversing a string, you do not need to operate after recursion , So before recursion

class Solution:
    def reverseString(self, s: List[str]) -> None:
        """ Do not return anything, modify s in-place instead. """
        def dfs(arr, l, r):
            if l >= r: #  The termination condition of recursion 
                return
            
            arr[l],arr[r] = arr[r],arr[l] #  Repeat the operation section . Swap the left and right characters 
            dfs(arr,l+1,r-1) #  Reduce the scale of the problem , Repeat 
        
        dfs(s,0,len(s)-1)
        return s

Reverse a linked list

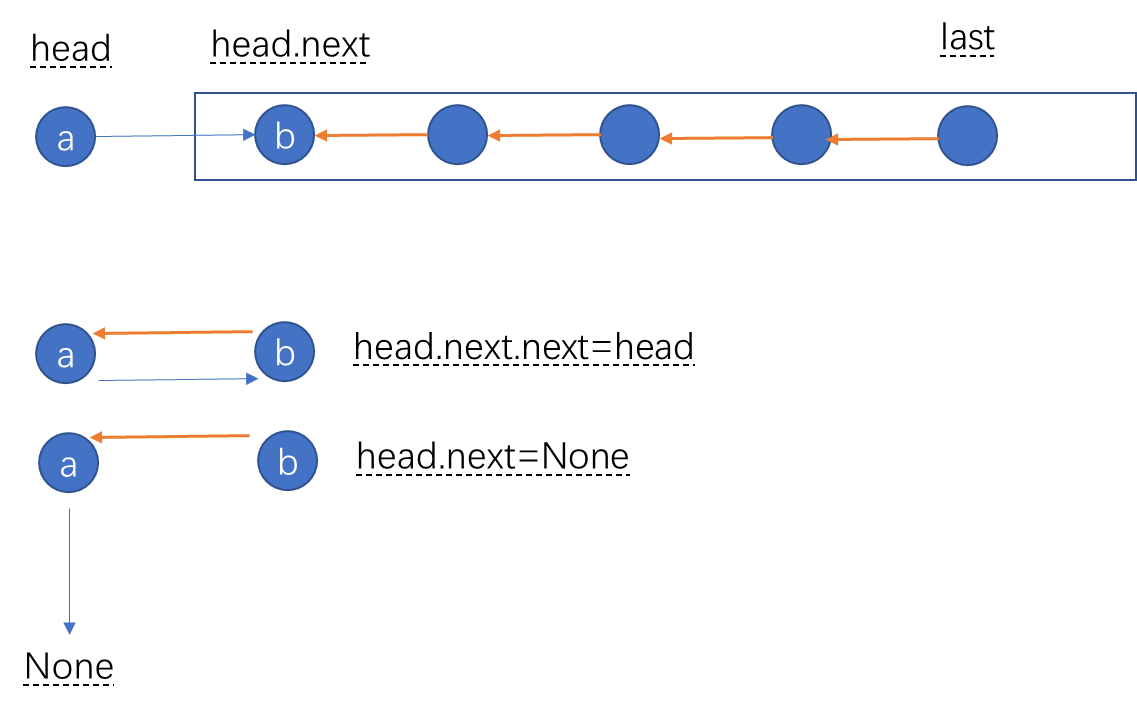
The inversion of the linked list can also be recursive , First, we need to find the last element , Then this element is the inverted head node , So we go back . Then we can reverse the elements , Suppose the follow-up has been reversed （ Recursion will be reversed one by one ）, Now? a How should this node be reversed ？a Of next yes b, The aim now is to make b Of next Point to a, In fact, it's very simple

b=a.next #  The goal is 
b.next=a #  The goal is to make b.next Point to a
a.next.next=a #  because a.next=b, So it can be written directly as 

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def reverseList(self, head: ListNode) -> ListNode:

        if head is None or head.next is None:
            return head
        last = self.reverseList(head.next)
        head.next.next = head
        head.next = None
        return last
        

Print linked list from end to end

Enter the head node of a linked list , Return the value of each node from the end to the end （ Return with array ）.

There are operations after recursive functions , That is to say, this recursive function keeps looking back , Finally found the stop condition , It will return at this time , Do some operations after returning , Here is to save the data .
And found a problem , The parameter we input is head, Then there is another recursive function head.next, That is to say, at this time, we are actually led by cur and next Of .

At first, recursion doesn't go from top to bottom , No operation is required , Go until you finally find the stop condition , Then start to return step by step , This time is from bottom to top （ The reverse is true ）, We take every step of head Just store it .

	1	2	3	4	5	None
	head
		head
			head
here head yes 4				head
here head yes 5, Pass in head.next					head
Stop conditions ,head is None						head

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None

class Solution:
    def reversePrint(self, head: ListNode) -> List[int]:
        res = []
        def dfs(head):
            if head is None:
                return
            
            dfs(head.next) # head.next is None, At this time, the stop condition is found 
            res.append(head.val) # head The value of is not None, So add values , And at this time, it starts to return recursively head, That's the last step head
        
        dfs(head)
        return res

Delete the last of the linked list N Nodes

The recursion of the linked list is more like recursive traversal , Not through for Loop operation to traverse , Directly use the principle of recursion to traverse , Delete the penultimate N When there are nodes , Recursion will traverse to the tail in a forward direction , Then return from the bottom up , At this time, we can count , Record to No N+1 When it's time , We can operate .

There are two tips , One is to define a dummy Put the node of head In front of , So if you want to delete head The node of can still return dummy.next, The second is to use nonlocal This keyword , This keyword defines that internal functions can operate on variables other than functions .

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        dummy = ListNode(0,head)
        def dfs(head):
            nonlocal n
            if head is None:
                return
            dfs(head.next)

            n -= 1
            if n == -1:
                head.next = head.next.next
        
        dfs(dummy)
        return dummy.next

Two or two exchange nodes in a linked list

This can also consider recursion , We first swap two nodes , The following nodes are all repeated operations , therefore , This problem can be solved by cycling , You can also use recursion , But this question needs to think about what to return .

How do we know this iterative formula ？ How to judge this problem is to use recursion ？ What if a big problem can't be broken down into a small problem ？

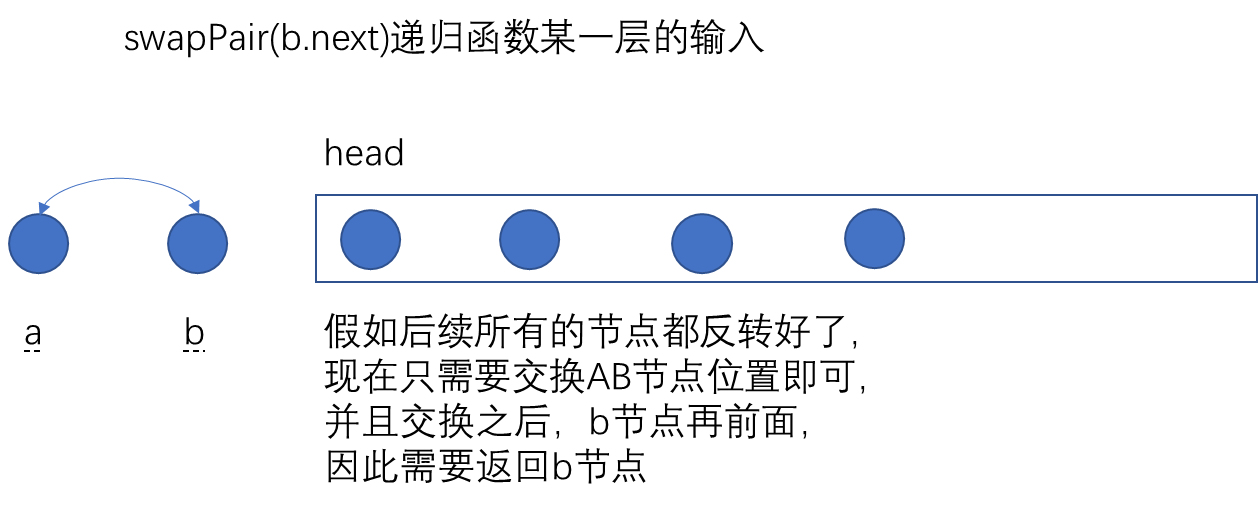
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
    def swapPairs(self, head: ListNode) -> ListNode:
        if head is None or head.next is None:
            return head
        a = head
        b = head.next
        
        a.next = self.swapPairs(b.next)
        b.next = a
        return b

2 The power of

Give you an integer n, Please judge whether the integer is 2 Power square

Recursion can also be considered for this problem , The big problem is to judge whether a number is 2 Power square , Divide this number by 2 The new number obtained later will also determine whether it is 2 Power square , That is, big problems can be broken down into small problems step by step , And every step is repeated , Repeat to judge whether it can be 2 to be divisible by

You can see that this problem directly returns the recursive function , And there is no other operation , This means that the result of recursion to the last layer is to return directly layer by layer , There is no middleman , So whether the last step can be divided directly is the final result .

I don't know n Whether it is 2 Power square , But if it can be solved n%2 To judge , If I know n%21, that n Definitely not 2 Power square , If n%20, I still don't know , But I can reduce the scale of the problem , If I know (n//2)%==1, that n Definitely not 2 Power square .

class Solution:
    def isPowerOfTwo(self, n: int) -> bool:
        if n == 1:
            return True
        elif n % 2 > 0 or n < 1:
            return False
        return self.isPowerOfTwo(n // 2)
        

Hanoi

Hanoi tower is also done in a recursive way . If we have N Disc , Let's go through C The former N-1 A disk moves to B above , And then put A The upper disc is moved to C above , And then we go through A, hold B On the top N-1 A disk moves to C above .
Why do you think of using recursion ？ Because the original problem is the same as the reduced problem , We can N Turn it into N-1,N-1 Turn it into N-2, Until 2,1 wait . In the same way , Recursion is actually very much like a recursive formula for high school learning , First, Zengming N=1 It is in accordance with the law , Then prove N+1 Is also in line with the law . That is to say, no matter how big the problem is , All conform to the same law , So we can calculate it iteratively .

There is another interesting place in Hanoi Tower , Our input is move(n,A,B,C), To get this result , So we recurse one in our function move(n-1.A,C,B), The question is how do we put n-1 A disc to move ？ I do not know! , So this is where recursion makes people confused , Can the problem be solved by recursion ？ Yes , That's it . Anyway, I haven't figured it out yet , adopt move(n-1.A,C,B) after ,A There is only one disc on it , At this point, we move this disc directly to C Just above . The problem is , I don't even know now C Is there a disc on it , Ask what you can move directly , Amazing .

class Solution:
    def hanota(self, A: List[int], B: List[int], C: List[int]) -> None:
        """ Do not return anything, modify C in-place instead. """

        def move(n,A,B,C):
            if n == 1: #  When there is one disc left , Direct will A The disc moves to C On 
                C.append(A.pop())
                return

            move(n-1, A, C, B) #  take A above n-1 Two disks pass through C, Move to B above 
            C.append(A.pop()) #  At this time A The last disc above moves to C Just above 
            move(n-1, B, A, C) #  here B It has n-1 Disc ,B Re pass A hold n-1 A disk moves to C Just above 
        
        n = len(A)
        move(n,A,B,C)
        

50. Pow(x, n)

This recursion is also very interesting , It's also a little hard to understand , We ask $x^n$ In fact, recursion can be divided into two cases
$$x^n=\{\begin{array}{ll}(x^{\frac{n}{2}}{)}^2& \text{n\%2==0}\\ x\ast (x^{\frac{n}{2}}{)}^2& \text{n\%2==1}\end{array}$$
The form of recursive function is
$$pow(x,n)=\{\begin{array}{ll}pow(x,n//2{)}^2& \text{n\%2==0}\\ x\ast pow(x,n//2{)}^2& \text{n\%2==1}\end{array}$$

You ask me how to solve $pow(x,n//2)$ I don't know either , Anyway, it can be solved by recursion according to this recursion formula . I don't know how to ask $pow(x,n)$, But if I find out $pow(x,n//2)$ I can work out $pow(x,n)$ 了 , Such as sum solution $pow(x,n//2)$ Well ？ I just want to solve $pow(x,n//4)$ That's all right. , In this way, the problem will eventually be reduced to n=1 That is, stop conditions , Then recursion returns , We can operate this to return the result .

This is very similar to the problem of Hanoi Tower , I don't know how to n A disk from A Move to C, But if I put n-1 A disc can move to B, Then it can be done .

class Solution:
    def myPow(self, x: float, n: int) -> float:

        def dfs(x,n):
            if n == 0:
                return 1
            y = dfs(x, n//2)
            if n % 2 == 0:
                return y * y
            else:
                return x * y * y
        
        if n < 0:
            x = 1 / x
            n = -n

        r = dfs(x,n)
        return r