当前位置:网站首页>递归:深度优先搜索
递归:深度优先搜索
2022-07-03 03:28:00 【我家大宝最可爱】
二叉树的最大深度
二叉树的问题一般都是优先考虑递归的,我们想要求出一棵树的深度,当我们知道了左子树和右子树的深度的时候,那么root节点的深度就是左右子树最大的值加1
d e p t h ( r o o t ) = m a x ( d e p t h ( r o o t . l e f t ) , d e p t h ( r o o t . r i g h t ) ) + 1 depth(root)=max(depth(root.left),depth(root.right))+1 depth(root)=max(depth(root.left),depth(root.right))+1
很明显这也是一个递归的式子,所以直接使用递归即可
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
def dfs(root):
if not root: # base case
return 0
l = dfs(root.left) # 先求左子树的深度
r = dfs(root.right) # 然后求右子树的深度
return max(l,r)+1 # 取最大,然后加上root节点就是+1
return dfs(root)
二叉树的最小深度
一开始觉得最小深度和最大深度是一样的,但是发现直接写min是有问题的。
最重要的问题是,最小深度是从叶子节点开始的,所以base case有两种,一个是head==None,另一种就是head.right is None and head.left is None。必须是从叶子节点开始。
错误写法,可以看到a节点,a节点的左子树深度是0,右子树深度是2,那么根据这个错误的递归式子可以得到a节点的最小深度为min(0,2)=0,但是很明显,a节点不是一个叶子节点,所以不能求最小深度的。但是最大深度不会有这样的问题。
class Solution:
def minDepth(self, root: TreeNode) -> int:
if root is None:
return 0
return min(self.minDepth(root.right),self.minDepth(root.left))+1

正确写法需要考虑某个子树为None的情况,这个时候需要递归另一边的子树作为最小深度。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: TreeNode) -> int:
if root is None:
return 0
elif root.left is None and root.right is None:
return 1
elif root.left is None:
return self.minDepth(root.right)+1
elif root.right is None:
return self.minDepth(root.left) + 1
else:
return min(self.minDepth(root.right),self.minDepth(root.left))+1
平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1
这个问题本质也是求解树的深度,只不过要求左右子树的深度差值不超过1,如果超过一就会直接返回False。同样的理解,我们想要知道root节点是平衡的,那么就需要计算左右子树的高度,计算完高度之后,还需要判断左右子树是否也是平衡二叉树,如果有一个不是的话,那么root肯定也不是
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
def dfs(root):
if not root:
return 0,True
l,lf = dfs(root.left)
r,rf = dfs(root.right)
if abs(l-r) <= 1 and lf and rf:
return max(l,r)+1,True
else:
return max(l,r)+1,False
_,f = dfs(root)
return f
完全二叉树的节点个数
统计个数也是非常的简单,我们统计左子树的个数然后加上右子树的个数,然后加上根节点一个就是总共的节点个数了。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: TreeNode) -> int:
if root is None:
return 0
return self.countNodes(root.left) + self.countNodes(root.right) + 1
边栏推荐
- Mysql Mac版下载安装教程
- Limit of one question per day
- Agile certification (professional scrum Master) simulation exercise-2
- labelimg生成的xml文件转换为voc格式
- PAT乙级“1104 天长地久”DFS优化思路
- Spark on yarn resource optimization ideas notes
- [set theory] partial order relation (partial order relation definition | partial order set definition | greater than or equal to relation | less than or equal to relation | integer division relation |
- Use three JS make a simple 3D scene
- umi 路由拦截(简单粗暴)
- MongoDB复制集【主从复制】
猜你喜欢
FileZilla Client下載安裝
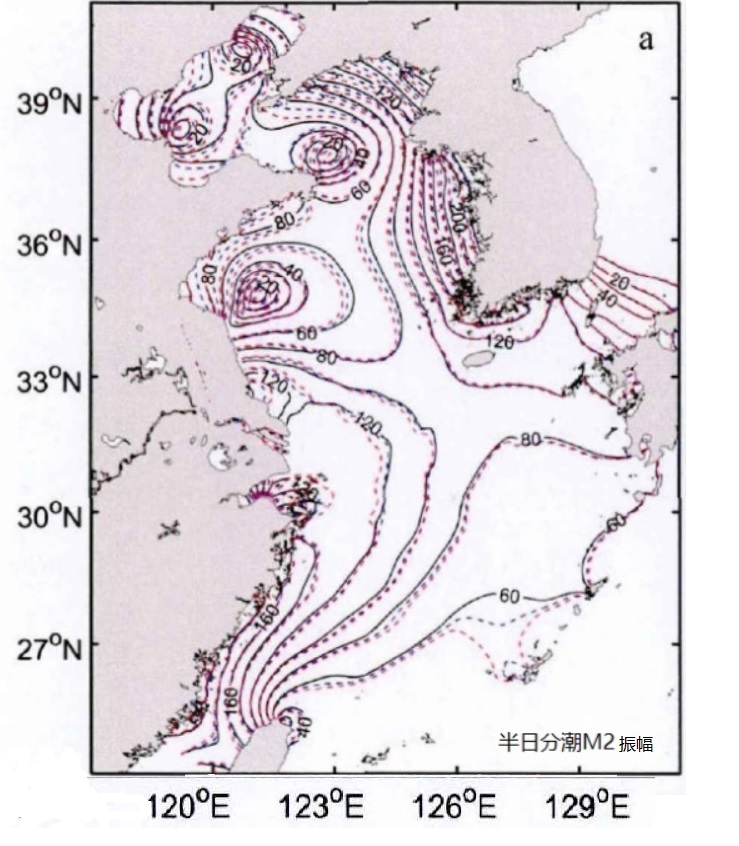
渤、黄海的潮汐特征

Pytorch轻量级可视化工具wandb(local)

Téléchargement et installation du client Filezilla

小程序获取用户头像和昵称
Unity3d RPG implementation (medium)
MySQL MAC download and installation tutorial

Application of derivative in daily question

Nasvit: neural architecture search of efficient visual converter with gradient conflict perception hypernetwork training
![MySQL practice 45 [global lock and table lock]](/img/23/fd58c185ae49ed6c04f1a696f10ff4.png)
MySQL practice 45 [global lock and table lock]
随机推荐
[mathematical logic] normal form (conjunctive normal form | disjunctive normal form | major item | minor item | maximal item | minor item | principal conjunctive normal form | principal disjunctive no
MySQL practice 45 [global lock and table lock]
C # webrequest post mode, based on "basic auth" password authentication mode, uploads files and submits other data using multipart / form data mode
Introduction to mongodb
User value is the last word in the competition of mobile phone market
PHP generates PDF tcpdf
@Accessors annotation function specifies that the prefix follows the hump naming
FileZilla Client下載安裝
MongoDB主配置文件
Pat class B common function Usage Summary
redis高级应用【密码防护、数据持久化、主从同步、哨兵模式、事务】【暂未完成(半成品)】
VS 2019安装及配置opencv
VS 2019 配置tensorRT生成engine
[combinatorics] Application of exponential generating function (multiple set arrangement problem | different balls in different boxes | derivation of exponential generating function of odd / even sequ
Téléchargement et installation du client Filezilla
QQ小程序开发之 一些前期准备:预约开发账号、下载安装开发者工具、创建qq小程序
Pytorch轻量级可视化工具wandb(local)
Converts a timestamp to a time in the specified format
Vs 2019 configuration tensorrt
解决高並發下System.currentTimeMillis卡頓