当前位置:网站首页>PAT乙级“1104 天长地久”DFS优化思路
PAT乙级“1104 天长地久”DFS优化思路
2022-07-03 03:07:00 【Sumzeek丶】
本文介绍了笔者对于B1104的优化思路,AC代码在文末Case3
如果您没有做出答案,笔者强烈建议你按需阅读Case1-3,在看完之后自己动手写一遍代码,自己思考优化思路,并动手实现,本文只起到一个抛砖引玉的作用,欢迎各位大神在评论区分享自己的优化思路。
“天长地久数”是指一个  位正整数
位正整数  ,其满足条件为:
,其满足条件为: 的各位数字之和为
的各位数字之和为  ,
, 的各位数字之和为
的各位数字之和为  ,且
,且  与
与  的最大公约数是一个大于 2 的素数。本题就请你找出这些天长地久数。
的最大公约数是一个大于 2 的素数。本题就请你找出这些天长地久数。
输入格式:
输入在第一行给出正整数  ,随后 N 行,每行给出一对
,随后 N 行,每行给出一对 和
和 ,其含义如题面所述。
,其含义如题面所述。
输出格式:
对每一对输入的  和
和  ,首先在一行中输出
,首先在一行中输出 Case X,其中 X 是输出的编号(从 1 开始);然后一行输出对应的  和
和  ,数字间以空格分隔。如果解不唯一,则每组解占一行,按
,数字间以空格分隔。如果解不唯一,则每组解占一行,按  的递增序输出;若仍不唯一,则按
的递增序输出;若仍不唯一,则按  的递增序输出。若解不存在,则在一行中输出
的递增序输出。若解不存在,则在一行中输出 No Solution。
输入样例:
2
6 45
7 80
输出样例:
Case 1
10 189999
10 279999
10 369999
10 459999
10 549999
10 639999
10 729999
10 819999
10 909999
Case 2
No Solution
Case 1:
看到这题笔者首先想到的是使用dfs回溯剪枝进行暴力求解,一共需要自定义三个函数
- isPrime():求素数
- gcd():求最大公因数
- dfs():回溯剪枝
然后通过dfs累加字符串s1,例如k=4,就尝试0000-9999之间的所有情况,最后判断边界条件
- 最大公因数是素数且大于2
- s1的各位相加等于m
若满足边界条件,则打印相应数据。
#include<bits/stdc++.h>
using namespace std;
int N, k, m, n;
string s1;
bool flag;
bool isPrime(int a) {
if (a == 0 || a == 1)return false;
for (int i = 2; i <= sqrt(a); i++) {
if (a % i == 0)return false;
}
return true;
}
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
int add(string s) {
int sum = 0;
for (int i = 0; i < s.length(); i++)
sum += s[i] - '0';
return sum;
}
void dfs(int step) {
if (step == k) {
int t = gcd(m, add(to_string(stoi(s1) + 1)));
if (t > 2 && add(s1) == m && isPrime(t)) {
printf("%d %s\n", add(to_string(stoi(s1) + 1)), s1.c_str());
flag = true;
}
return;
}
for (int i = 0; i <= 9; i++) {
s1 += i + '0';
dfs(step + 1);
s1.erase(s1.length() - 1);
}
}
int main() {
cin >> N;
int i;
for (i = 0; i < N; i++) {
cin >> k >> m;
s1 = "";
flag = false;
printf("Case %d\n", i + 1);
dfs(0);
if (!flag) cout << "No Solution\n";
}
return 0;
}以下是运行结果,有两个测试点超时,但基本逻辑没问题,故需要优化算法。
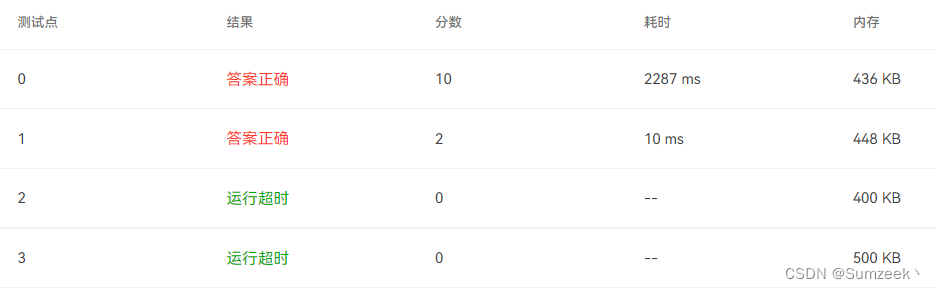
Case 2:
我首先想到的是使用一个tepm记录s1字符串还可以使用的最大长度,例如输入(6,44),s1长度为6的时候各位相加必须等于44,假如当s1=99999时,s1的长度只有5但是s1各位累加已经为45,故没有往后尝试的必要(剪枝),可以减少算法运行的时间,同时在dfs中判断边界条件时,有一些语句是冗余的,运算了两次,故也可以用一个临时变量存储,避免多次运算。
#include<bits/stdc++.h>
using namespace std;
int N, k, m, n;
int tmpm;
string s1;
bool flag;
bool isPrime(int a) {
if (a == 0 || a == 1)return false;
for (int i = 2; i <= sqrt(a); i++) {
if (a % i == 0)return false;
}
return true;
}
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
int add(string s) {
int sum = 0;
for (int i = 0; i < s.length(); i++)
sum += s[i] - '0';
return sum;
}
void dfs(int step) {
if (step == k) {
int n1 = add(to_string(stoi(s1) + 1));
int t = gcd(m, n1);
if (t > 2 && 0 == tmpm && isPrime(t)) {
printf("%d %s\n", n1, s1.c_str());
flag = true;
}
return;
}
for (int i = 0; i <= 9; i++) {
s1 += i + '0';
tmpm -= i;
if (tmpm >= 0)
dfs(step + 1);
tmpm += i;
s1.erase(s1.length() - 1);
}
}
int main() {
cin >> N;
int i;
for (i = 0; i < N; i++) {
printf("Case %d\n", i + 1);
cin >> k >> m;
tmpm = m;
if (k * 9 < m)
cout << "No Solution\n";
else {
s1 = "";
flag = false;
dfs(0);
if (!flag) cout << "No Solution\n";
}
}
return 0;
}
虽然测试点0的耗时降低了,但是测试点2,3还是超时,故还需要优化思路。
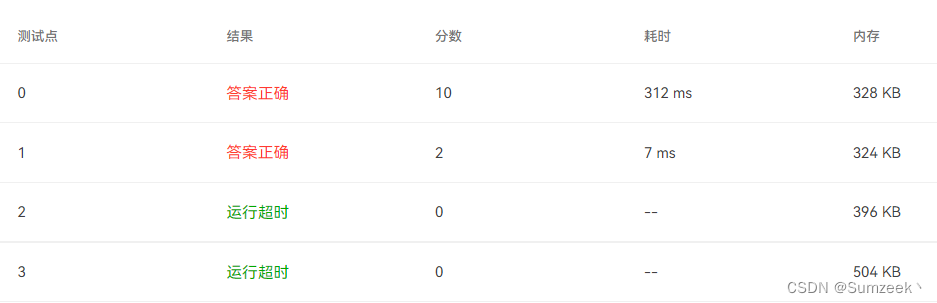
Case 3:
本次优化思路来源于老帅比阿的博客,在审题时我们忽略了一个十分重要的点,那就是m和n的最大公因数必须大于2,容易得知s1最后结果的个位一定需要是9,如若不是9则n=m+1,那么n与m的最大公因数一定只能是1,因为相邻两个正整数的最大公因数是1,只有s1的末位是9或末尾是连续的9,加一之后末尾变为0才有可能使m与n的最大公因数大于2。
我们还忽略的题目的一个条件,那就是结果按照n的大小升序排列,故使用矢量组存储结果,再对矢量组进行排序输出,即可得出结果。
#include<bits/stdc++.h>
using namespace std;
int N, k, m, n;
int tmpm;
string s1;
struct node {
int n;
string s;
}tmp;
vector<node> v;
bool cmp(node a, node b) {
if (a.n != b.n) return a.n < b.n;
else return a.s < b.s;
}
bool isPrime(int a) {
if (a == 0 || a == 1)return false;
for (int i = 2; i <= sqrt(a); i++) {
if (a % i == 0)return false;
}
return true;
}
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
int add(string s) {
int sum = 0;
for (int i = 0; i < s.length(); i++)
sum += s[i] - '0';
return sum;
}
void dfs(int step) {
if (tmpm < 0)
return;
if (step == k - 2) {
s1 += "99";
int n1 = add(to_string(stoi(s1) + 1));
int t = gcd(m, n1);
if (t > 2 && 0 == tmpm && isPrime(t)) {
tmp.n = n1; tmp.s = s1;
v.push_back(tmp);
}
s1.erase(s1.length() - 2);
return;
}
for (int i = 0; i <= 9; i++) {
s1 += i + '0';
tmpm -= i;
dfs(step + 1);
tmpm += i;
s1.erase(s1.length() - 1);
}
}
int main() {
cin >> N;
int i, j;
for (i = 0; i < N; i++) {
printf("Case %d\n", i + 1);
cin >> k >> m;
tmpm = m - 18;
if (k * 9 < m)
cout << "No Solution\n";
else {
s1 = "";
v.clear();
dfs(0);
if (v.size() == 0) cout << "No Solution\n";
else {
sort(v.begin(), v.end(), cmp);
for (j = 0; j < v.size(); j++)
printf("%d %s\n", v[j].n, v[j].s.c_str());
}
}
}
return 0;
}
优化之后的算法可以跑过测试点2,3 ,达成AC。
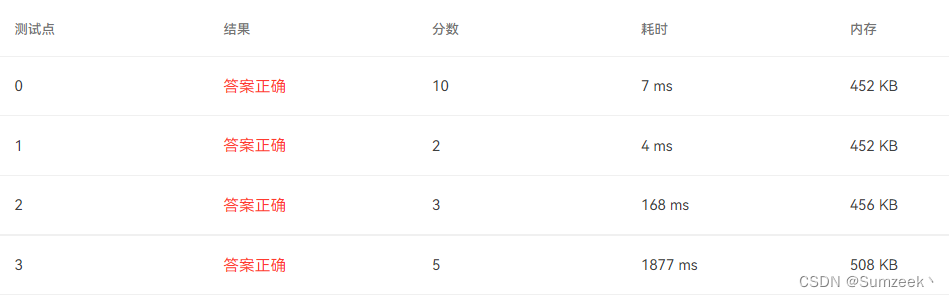
边栏推荐
- 迅雷chrome扩展插件造成服务器返回的数据js解析页面数据异常
- I2C subsystem (II): I3C spec
- Reset or clear NET MemoryStream - Reset or Clear . NET MemoryStream
- Spark on yarn资源优化思路笔记
- Are there any recommended term life insurance products? I want to buy a term life insurance.
- Docker install MySQL
- Source code analysis | resource loading resources
- Source code analysis | layout file loading process
- Kubernetes family container housekeeper pod online Q & A?
- MySQL practice 45 [SQL query and update execution process]
猜你喜欢

I2C subsystem (I): I2C spec
![[error record] the parameter 'can't have a value of' null 'because of its type, but the im](/img/1c/46d951e2d0193999f35f14d18a2de0.jpg)
[error record] the parameter 'can't have a value of' null 'because of its type, but the im
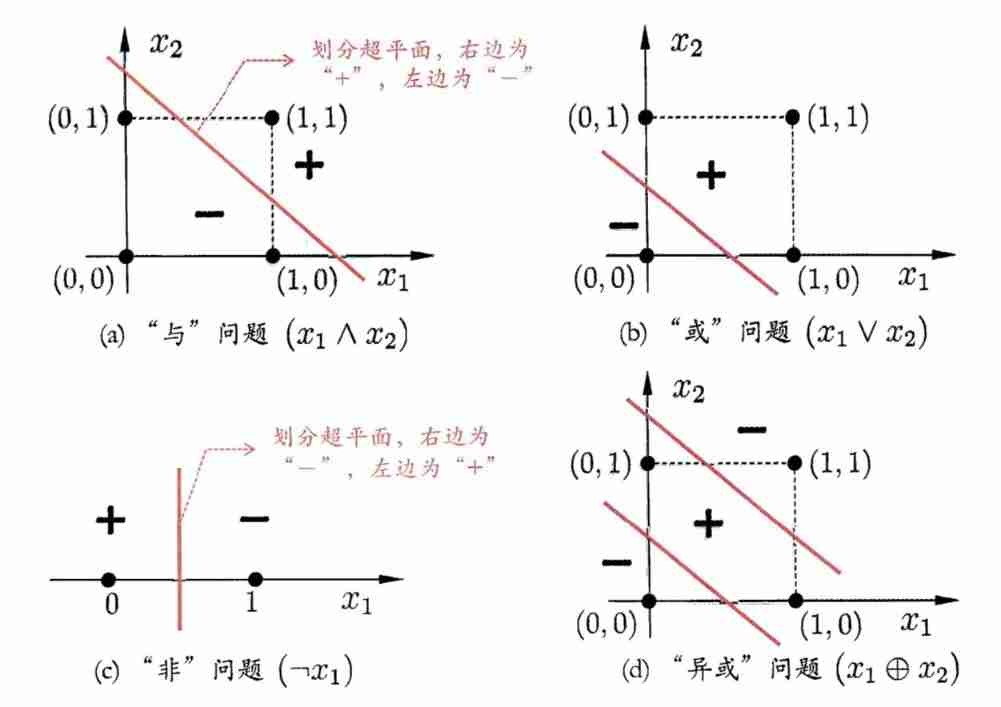
Deep learning: multi-layer perceptron and XOR problem (pytoch Implementation)
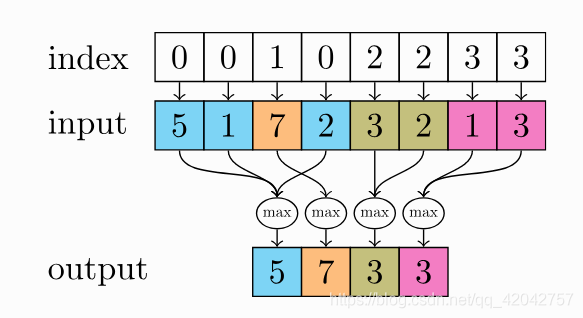
【PyG】理解MessagePassing过程,GCN demo详解

Three. JS local environment setup
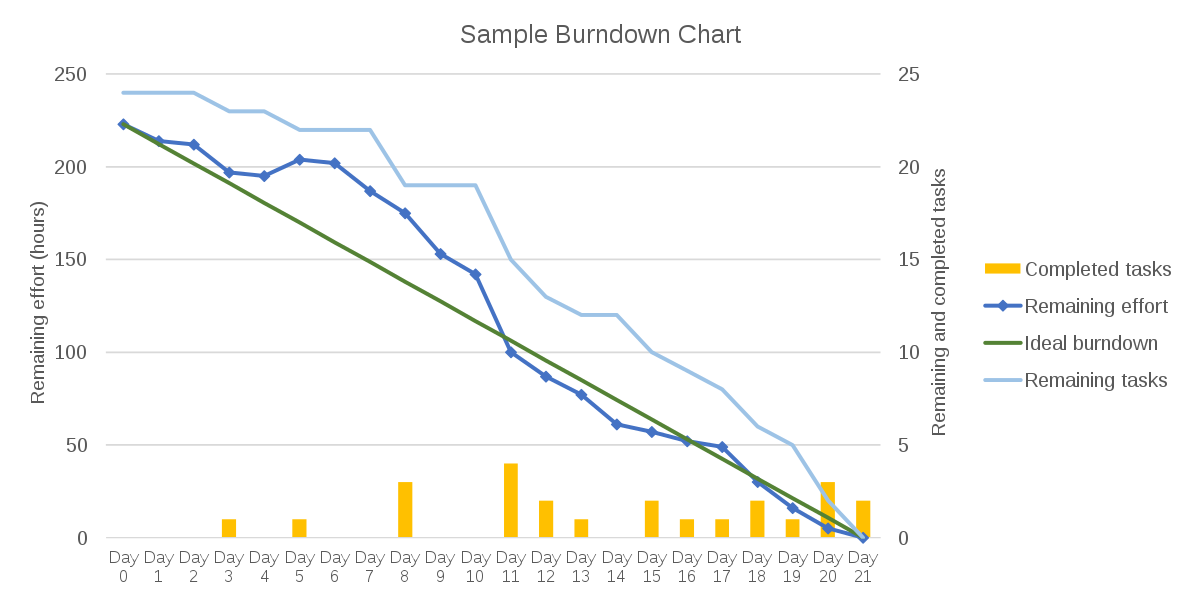
Agile certification (professional scrum Master) simulation exercise-2
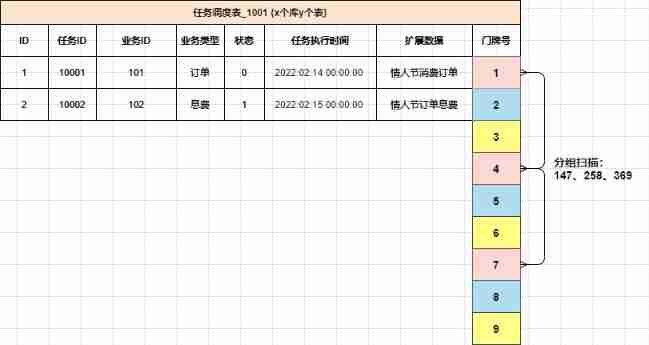
Add some hard dishes to the interview: how to improve throughput and timeliness in delayed task scenarios!
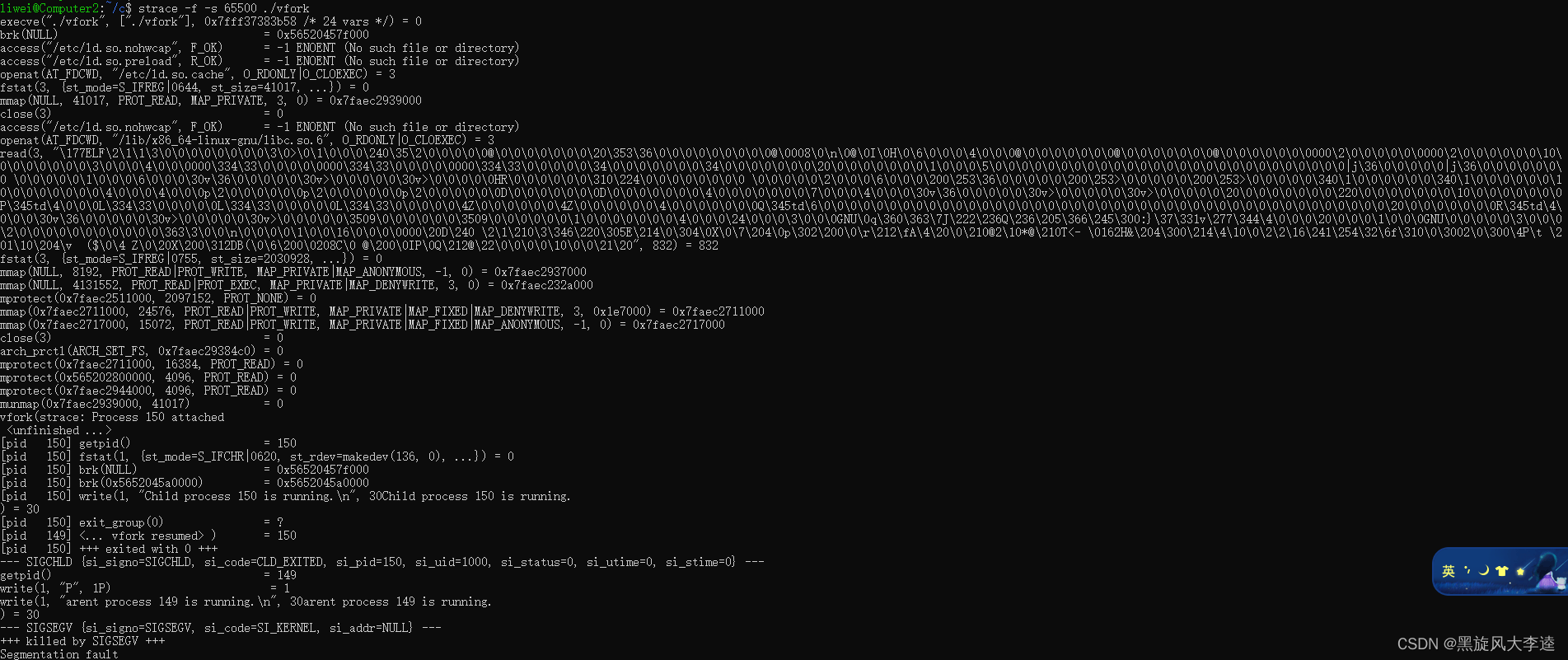
vfork执行时出现Segmentation fault

MySql实战45讲【全局锁和表锁】
Add automatic model generation function to hade
随机推荐
[shutter] monitor the transparency gradient of the scrolling action control component (remove the blank of the top status bar | frame layout component | transparency component | monitor the scrolling
How to limit the size of the dictionary- How to limit the size of a dictionary?
labelme标记的文件转换为yolov5格式
基于Qt的yolov5工程
Andwhere multiple or query ORM conditions in yii2
Check log4j problems using stain analysis
Deep Reinforcement Learning for Intelligent Transportation Systems: A Survey 论文阅读笔记
BigVision代码
MySQL Real combat 45 [SQL query and Update Execution Process]
Are there any recommended term life insurance products? I want to buy a term life insurance.
Three. JS local environment setup
Concrete CMS vulnerability
Nasvit: neural architecture search of efficient visual converter with gradient conflict perception hypernetwork training
Add automatic model generation function to hade
Update and return document in mongodb - update and return document in mongodb
Check log4j problems using stain analysis
What is the way out for children from poor families?
Use optimization | points that can be optimized in recyclerview
Privatization lightweight continuous integration deployment scheme -- 01 environment configuration (Part 2)
MySQL practice 45 [SQL query and update execution process]