Overview of Fourier analysis

   Fourier transform is mainly divided into two parts: continuous and discrete . Analysis of continuous time signals , From the Fourier series of periodic signals （FS） Expand to the unified Fourier transform （FT）, It is a complete system . Fourier analysis of discrete-time signals is very similar to that of continuous time signals , But it's really different , There is no unified expression , The main difference is “ Sum up ” and “ integral ” On .FS,FT,DFS,DTFT,DFT It forms the whole system of Fourier analysis .
   No matter what kind of transformation , All satisfied with “ cycle - discrete ”,“ Aperiodic - continuity ” Correspondence of . This relationship is very useful for helping memory .

Analysis method	abbreviation	The transformation process Time domain signal → Frequency domain signal
Fourier series	FS	Continuous period → Aperiodic discrete
The Fourier transform	FT	（ introduce $\delta (\omega )$） Continuous period → Aperiodic discrete Continuous aperiodic → Aperiodic continuous
Discrete Fourier series	DFS	Discrete period → Periodic discretization
Discrete time Fourier transform	DTFT	Discrete aperiodic → Periodic continuity
Discrete Fourier transform	DFT	Discrete aperiodic → Discrete aperiodic ( The essence ) Discrete period → Periodic discretization

Continuous time Fourier analysis

Fourier series

   Continuous time analysis starts with Fourier series .

$$f(t)=f(t+T_0)f(t)=\sum _{n=-\infty }^{+\infty }{a}_n{e}^{-jn{\omega }_0}$$

   Any period is $T_0$（ The frequency is $f_0$, Angular frequency is ${\omega }_0$） The periodic signal of , Can use angular frequency ${\omega }_0$ Integer multiple complex exponential signal $e^{-jn{\omega }_0}$ Linear representation .
   Such as cosine signal $Acos({\omega }_{0}t)$ Fourier series expansion can be expressed as ：
$$Acos({\omega }_{0}t)=\frac{A}{2}\left(e^{-j{\omega }_{0}t}+e^{j{\omega }_{0}t}\right)$$

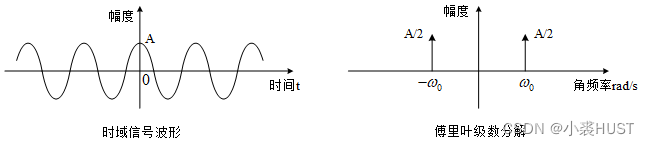
   The amplitude spectrum obtained by Fourier transform of real signal is always even symmetric , The phase spectrum is always odd symmetric . A cosine signal can be decomposed into two conjugate complex exponential signals , As shown in the figure below .

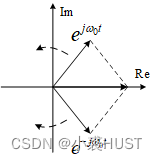
   Over time $t$ An increase in , They rotate constantly on the complex plane , But their vector sum always falls on the real axis , External performance is a real signal .
   That's why “ Negative frequency ” The reason for its existence , there “ negative ” It means that the angular frequency of the complex exponential signal is negative , And “ Positive frequency ” The signal of is conjugate . Complex exponential signals that are conjugate with each other form a real signal .

The Fourier transform

   Fourier series is limited to the analysis of periodic signals , For aperiodic signals , The period of the signal can be regarded as infinity , Based on this idea , It can be extended from the analytical synthesis formula of Fourier series to Fourier transform pair . The following is the analytical synthesis formula of Fourier series ：

$$a_n=\frac{1}{T_0}\underset{T_0}{\int }f(t)e^{-jn{\omega }_{0}t}dtf(t)=\sum _{n=-\infty }^{+\infty }{a}_n{e}^{jn{\omega }_0}$$

  $a_n$ Represents the Fourier series with the fundamental wave $n$ Coefficient of complex exponential signal of subharmonic relationship . Write them together to get ：

$$f(t)=\sum _{n=-\infty }^{+\infty }\left(\frac{1}{T_0}\underset{T_0}{\int }f(t)e^{-jn{\omega }_{0}t}dt\right)e^{jn{\omega }_0}$$

$$={\int }_{-\infty }^{+\infty }\left({\int }_{-\infty }^{+\infty }f(t)e^{-jn{\omega }_{0}t}dt\right)e^{jn{\omega }_0}df$$

   When $T_0$ Towards infinity ,$f_0$ Tends to infinity , The original sum needs to be changed to integral , The differential variable is from the original $1/T_0$ Transformed $df$.

$$=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }\left({\int }_{-\infty }^{+\infty }f(t)e^{-jn{\omega }_{0}t}dt\right)e^{jn{\omega }_0}d\omega$$

  $df$ To $d\omega$ It needs to be multiplied by $2\pi$, So there is one in the synthesis of the last Fourier transform $1/2\pi$ The coefficient of .

$$X(j\omega )={\int }_{-\infty }^{+\infty }f(t)e^{-j\omega t}dtf(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }X(j\omega )e^{j\omega t}d\omega$$

Unity of periodic and aperiodic signals

   After introducing the impulse signal $\delta (t)$ after , The Fourier transform of periodic signal and aperiodic signal is unified . The problem of Fourier transform of periodic signals is that the analytical formula of Fourier transform is an integral in infinite range , Periodic signals cannot converge when doing such integrals .
   Periodic signals can be decomposed into the sum of multiple complex exponential signals . So as long as we can express the Fourier transform of complex exponential signal, we can get the Fourier transform of periodic signal . Combined with the frequency shift property of Fourier transform ：

$$e^{j{\omega }_{0}t}x(t)\iff X\left(j\left(\omega -{\omega }_0\right)\right)$$

   We just need to know "1" The Fourier transform of the complex exponential signal can be obtained by the Fourier transform of . The specific solution process has been written , article A relatively complete derivation process is given in , I won't go into details here , The result is the following ：

$$1\iff 2\pi \delta \left(\omega \right)$$

   This result is also quite natural , hold $2\pi \delta \left(\omega \right)$ It is obvious that it can be established by substituting it into the Fourier transform synthesis .

$$\mathcal{F}\left(A\cos ({\omega }_{0}t)\right)=\frac{A}{2}\cdot 2\pi \delta \left(\omega -{\omega }_0\right)+\frac{A}{2}\cdot 2\pi \delta \left(\omega +{\omega }_0\right)$$

   Therefore, the result of Fourier transform of periodic signal will include $2\pi \delta \left(\omega -{\omega }^{\prime }\right)$ Impulse signal of , And the coefficients in front of each impulse signal are exactly the coefficients of the corresponding Fourier series .

Discrete time Fourier transform

   Discrete time Fourier transform and continuous time Fourier transform have many similarities , But they are two completely different analysis systems , The biggest difference is from “ integral ” Change into “ Sum up ”.

Discrete Fourier series

   The essence of Fourier transform is orthogonal decomposition of signal in frequency domain . In the case of continuous time signals , For a frequency of ${\omega }_0$ For periodic signals , Is to project it onto ${\omega }_0$、$2{\omega }_0$、$3{\omega }_0$ Wait for these frequencies that have a harmonic relationship with the fundamental frequency .
   In the case of continuity , Harmonics are infinite . And in discrete cases , The period is $N$ A sequence of numbers , The fundamental frequency can be expressed as $2\pi /N$, Due to the periodicity of complex exponential signals ：

$$e^{-j2\pi /N}=e^{-j2\pi (N+1)/N}$$

   So in the case of discrete , One cycle is N Sequence , It can only be decomposed into N Different complex exponential sequences .

$$\tilde{X}[k]=\sum _{n=0}^{N-1}\tilde{x}[n]W_N^{kn}\tilde{x}[n]=\frac{1}{N}\sum _{n=0}^{N-1}\tilde{X}[k]W_N^{-kn}$$

   The above is the analytical formula and synthetic formula of discrete Fourier series ,$W_N^{kn}$ It's right $e^{-j2\pi \frac{kn}{N}}$ A short note of , Also called rotation factor .
   Discrete Fourier series , Both the digital sequence in time domain and the complex exponential sequence in frequency domain are periodic ,$\tilde{x}[n]$ and $\tilde{X}[n]$ The wavy lines on the indicate that they are periodic signals .

Discrete Fourier transform

   First, the analytical formula and synthetic formula of discrete Fourier transform are given directly ：

$$X[k]=\sum _{n=0}^{N-1}x[n]W_N^{kn},0\le k\le N-1$$
$$x[n]=\frac{1}{N}\sum _{n=0}^{N-1}X[k]W_N^{-kn},0\le n\le N-1$$

   Discrete Fourier transform is also used to deal with the analysis of aperiodic sequences , Here we simply regard aperiodic sequence as periodic sequence , It is equivalent to intercepting a sequence of period length from discrete Fourier series to express . This is it. DFT Inherent periodicity .

Discrete time Fourier transform

   The textbook says DFT I also mentioned before DTFT, This is the orthodox method of analyzing the spectrum of finite length sequences . It is also through discrete Fourier series , Make N Going to infinity . Here is DTFT Analytical formula and synthetic formula of ：

$$x[n]=\frac{1}{2\pi }\underset{2\pi }{\int }X\left(e^{j\omega }\right)e^{j\omega n}d\omega X\left(e^{j\omega }\right)={\sum }_{n=-\infty }^{+\infty }x[n]e^{-j\omega n}$$

  DTFT The spectrum obtained is a periodic continuous spectrum , And it is based on $2\pi$ For cycles , It looks like this ：

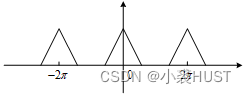
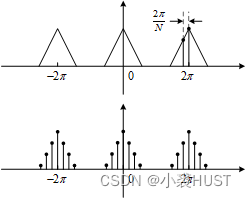
   If we take this finite sequence according to its length $N$ Carry out periodic continuation , It is equivalent to combining it with a cycle as $N$ Impulse string of （ A sequence of unit impulse functions ） Convolution . Time domain convolution is equivalent to frequency domain multiplication . The period of time domain is $N$ In the frequency domain, the period of the impulse string is $2\pi /N$ Impulse string of . therefore Finite sequence DFT Equivalent to DTFT Sampling on the spectrum of .