当前位置:网站首页>關於數據在內存中的存儲下
關於數據在內存中的存儲下
2022-06-25 13:10:00 【LIn_jt】
關於數據在內存中的存儲下
本文將講解浮點數在內存中存儲的相關知識
首先,先來看一下以下這個程序:>

在學習的時候, 我給出的答案是非常的單純的9 9.0 9 9.0,然而,當程序跑起來之後:>

要分析以上程序, 首先得了解浮點數在內存中的存儲。
對於二進制浮點數, 根據國際標准IEEE(電氣和電子工程協會) 754, 任意一個二進制浮點數V都能錶示為以下形式:>
*(-1) ^S * M 2 ^E
其中(-1)^S為符號比特,當s = 0 時,V為正數, 當浮點數s = 1 , V為負數.
M為有效比特, M>=1且M < 2
2 ^E次方錶示指數比特
舉個例子:>
例如十進制浮點數 5.5,我們將其轉換為二進制就為:>
101.1 //這裏是 .1的原因是此處1的權重是2 ^-1次方,即為0.5.而我們用上面V的格式,就能這樣寫:>
*(-1)^0 1.011 * 2 ^ 2
即S = 0; M = 1.011; E = 2;
對於-5.5,用上面V的格式, 就可以錶示為
*(-1)^1 (1.011) * 2 ^2;
對於浮點數在內存中的存儲,有以下規定
對於單精度浮點數而言

對於雙精度浮點數:>

此外還有一些規定: 因為M總是>=1 小於2, 即M永遠是等於1的整數, 因此,在內存中存放時,只會存小數比特,例 5.5
可以錶示為**(-1)^0 1.011 * 2 ^ 2*, M = 1.011。 但我們存儲的收, 只會存儲011, 而當我們去使用的時候, 才會把1給補上。
對於指數E而言, 其首先是一個unsigned int類型的數, 因此它的範圍為 0 ~ 255(8bit) 或者 0 ~2047(11bit)
而用科學計數法錶示的時候, 難免會出現E為負數的情况 例如 十進制0.5 用二進制數錶示為:>
1*10 ^-1 又E的範圍大於等於0, 因此, 規定存入內存E的真實值必須再加上一個中間數, 即加127 (8bit) 或1023(11bit)後,再存入內存
例如剛才的-1.,保存成32比特浮點數時, 保存為 -1 + 127 = 126即
01111110
此外, 指數E還有以下規定:>
若E的值不全為1或0, 則E的真實值就為內存中存儲的值减去127(或1023),再將有效數字M前加上第一比特的一。
例如剛才的0.5 二進制V錶示為:>
1.0*2 ^ -1 此處E為-1, M為1.0,因此存進內存中的數據為
0 01111110 00000000000000000000000
若E中存儲的數據為全0時, 那麼我們想一下, 則將是一個多麼小的數字!,即2^ -127次方, 因此, 規定如下:>
當E中存儲的數據為全0時, 其指數E的真實值為 1 - 127(或1023), 且有效數字M前不再加上一, 而是加上0, 以此來錶示一個接近0的數。
當E中存儲的數據為全一時, 那麼E的真實值為128(8bit), 那麼2^E次方是一個非常大的數字, 因此,V錶示為正負無窮大。
現在我們重新回到開頭的第一道例題:>
#include <stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值為:%d\n", n);
printf("*pFloat的值為:%f\n", *pFloat);
*pFloat = 9.0;
printf("num的值為:%d\n", n);
printf("*pFloat的值為:%f\n", *pFloat);
return 0;
}

再看一下第二部分:>

以浮點數的形式將n改成了9.0,那麼9.0的二進制錶示為:>
1001.0即1.001*2^3 那麼S = 0; E = 3 + 127 = 130; M = 0.001.即
0 1000 0010 00100000000000000000000
因此以整數的形式來看,這個數據為:>
![[外鏈圖片轉存失敗,源站可能有防盜鏈機制,建議將圖片保存下來直接上傳(img-Lw2C6Cbn-1638165164585)(C:\Users\MSI-NB\AppData\Roaming\Typora\typora-user-images\image-20211129090318437.png)]](/img/80/a182c36b6a88835bfbf0b336075649.png)
以浮點數的形式來看, 當然是9.0了。
边栏推荐
- 《MongoDB入门教程》第01篇 MongoDB简介
- [visio] solving the fuzzy problem of parallelogram in word
- Django框架——缓存、信号、跨站请求伪造、 跨域问题、cookie-session-token
- 英语口语 - 连读
- [turn] starting from the end, analyze in detail how to fill in the college entrance examination volunteer
- torch.tensor拼接与list(tensors)
- 剑指 Offer 04. 二维数组中的查找
- LeetCode链表题解技巧归纳总结
- 解析数仓lazyagg查询重写优化
- Native JS --- infinite scrolling
猜你喜欢
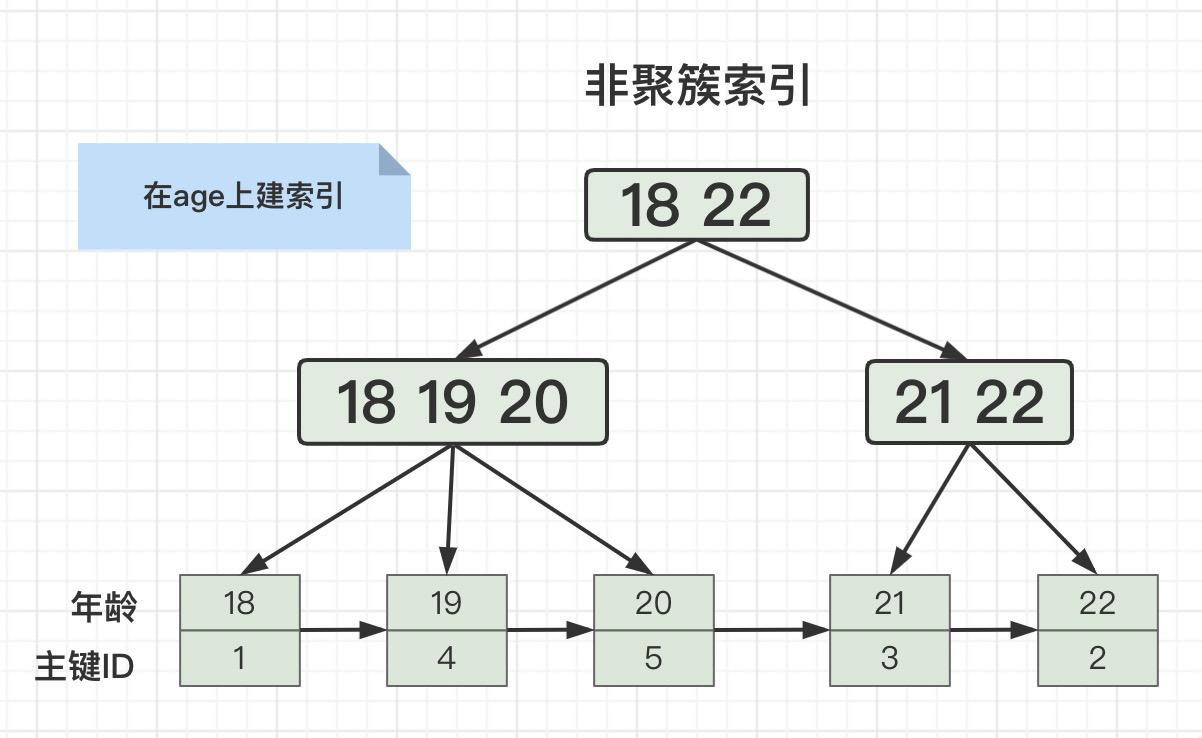
一篇文章讲清楚MySQL的聚簇/联合/覆盖索引、回表、索引下推

It is extraordinary to make a move, which is very Oracle!
Using CMD (command prompt) to install MySQL & configure the environment

解析數倉lazyagg查詢重寫優化

《MongoDB入门教程》第01篇 MongoDB简介

Drawing cubes with Visio

Optimization of lazyagg query rewriting in parsing data warehouse

Sword finger offer day 3 string (simple)

关于数据在内存中的存储下

nacos无法修改配置文件Mysql8.0的解决方法
随机推荐
1024水文
@Scheduled implementation of scheduled tasks (concurrent execution of multiple scheduled tasks)
Sword finger offer day 2 linked list (simple)
Analyse de l'optimisation de la réécriture des requêtes lazyagg de l'entrepôt
中国虚拟人哪家强?沙利文、IDC:小冰百度商汤位列第一梯队
几分钟上线一个网站 真是神器
Geospatial search: implementation principle of KD tree
Wechat full-text search technology optimization
德国举行全球粮食安全团结会议
剑指 Offer II 032. 有效的变位词
Baidu search stability analysis story
Sword finger offer II 025 Adding two numbers in a linked list
[machine learning] parameter learning and gradient descent
15 basic SEO skills to improve ranking
KVM script management - the road to dream
You can't specify target table 'xxx' for update in from clause
Seven competencies required by architects
剑指 Offer 04. 二维数组中的查找
用include what you use拯救混乱的头文件
list. replace, str.append