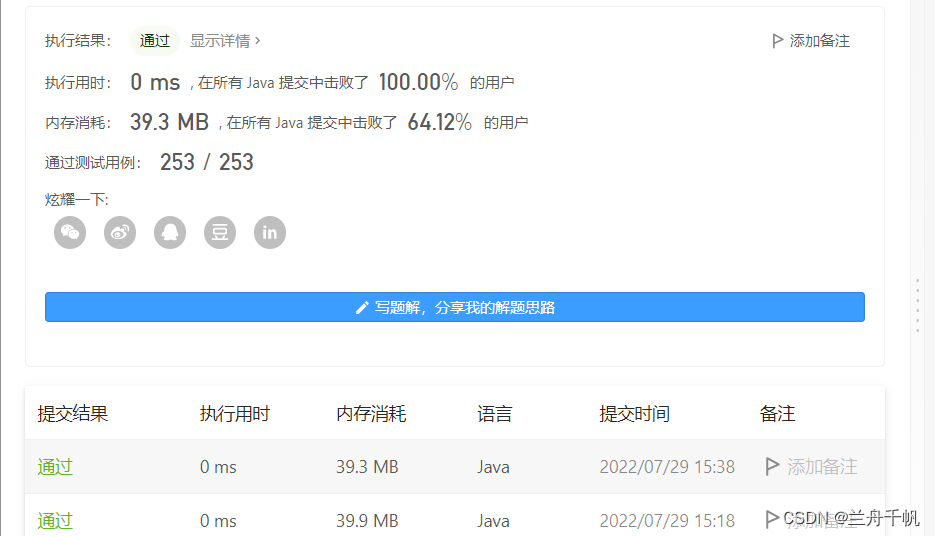
当前位置:网站首页>力扣刷题之有效的正方形(每日一题7/29)
力扣刷题之有效的正方形(每日一题7/29)
2022-07-31 01:47:00 【兰舟千帆】
力扣刷题之有效的正方形(每日一题7/29)
本题我采用的完全的计算暴力。
题目地址如下
链接
题目要求如下
给定2D空间中四个点的坐标 p1, p2, p3 和 p4,如果这四个点构成一个正方形,则返回 true 。
点的坐标 pi 表示为 [xi, yi] 。输入 不是 按任何顺序给出的。
一个 有效的正方形 有四条等边和四个等角(90度角)。
来源:力扣(LeetCode)


这是基本的要求。其实呢!提示我也没有去用,因为我采用的是完全的纯数学计算,用到了坐标的特点。比较暴力,代码快大,但是效率就是高。
下面是我的代码
class Solution {
public boolean validSquare(int[] p1, int[] p2, int[] p3, int[] p4) {
boolean result = judge_finally(p1,p2,p3,p4);
return result;
}
public static boolean judge_finally(int[]p1,int[]p2,int[]p3,int[]p4) {
double v_1_2 = judge_rhomb(p1, p2);//这里计算了一些可能用到的距离
double v2_3 = judge_rhomb(p2, p3);
double v3_4 = judge_rhomb(p3, p4);
double v1_4 = judge_rhomb(p1, p4);
double v_2_4 = judge_rhomb(p2, p4);
double v_1_3 = judge_rhomb(p1, p3);
//这里列出了可能构成的对角线,并作出对角线的判断,包括四点对角线中点重合,确认四边形
//距离相等以及对角线垂直约束。这样就逐步约束为正方形
//注意约束零点坐标,所以必须做一个约束,这里约束了对角线距离不为0
if (v_1_3 == v_2_4 && v_1_3 != 0&&judge_vertical(p1, p3, p2, p4)&judge_if_line(p1,p3,p2,p4)) {
return true;
}
if (v1_4 == v2_3 && v1_4 != 0&&judge_vertical(p1, p4, p2, p3)&judge_if_line(p1,p4,p2,p3)) {
return true;
}
if (v_1_2 == v3_4 && v_1_2 != 0&&judge_vertical(p1, p2, p3, p4)&judge_if_line(p1,p2,p3,p4)) {
return true;
}
return false;
}
public static double judge_rhomb(int[]a,int[]b)//计算两坐标构成线的长度
{
double x1 = ( Math.pow(a[0]-b[0],2)+Math.pow(a[1]-b[1],2));
return x1;
}
public static boolean judge_vertical(int[]a,int[]b,int[]c,int[]d)//判断直角
{
int v[] = {
a[0]-b[0],a[1]-b[1]};
int v1[] = {
c[0]-d[0],c[1]-d[1]};
return v[0]*v1[0]+v[1]*v1[1]==0;
}
public static boolean judge_if_line(int[]a,int[]b,int[]c,int[]d)//判断四点能否构成平行四边形
//如果四点可以构成平行四边形,则对角线中点重合
{
boolean bool_line_ = a[0] + b[0] == c[0] + d[0];
boolean bool_line__ = a[1]+b[1]==c[1]+d[1];
if (bool_line_&&bool_line__)
{
return true;
}
return false;
}
}
归结方法,很基础的方法
调用判断。这里的垂直用到了向量的特点。
x1x2+y1y2=0,这样就可以判断是否垂直。
对坐标四点判断是否构成平行四边形,需要判断对可能情况的对角线的中点是否重合,那么这里只要分别计算横纵坐标死否分别相等就行。
菱形的对角线是互相垂直平分的,我们只要在让它的对角线相等,就可以判断为正方形。但是要注意做这些给出的坐标约束。所以我给了对角线长度不为0。因为如果四个点的横纵坐标都为0的话,上面的要求其实是都可以满足的。
完全的对对角线的约束。
边栏推荐
- 进程间通信学习笔记
- leetcode-952: Calculate max component size by common factor
- 第一学年课程期末考试
- What have I experienced when I won the offer of BAT and TMD technical experts?
- 斩获BAT、TMD技术专家Offer,我都经历了什么?
- Kyushu cloud as cloud computing standardization excellent member unit
- 《云原生的本手、妙手和俗手》——2022全国新高考I卷作文
- 华为od 转骰子 js
- 软件测试缺陷报告---定义,组成,缺陷的生命周期,缺陷跟踪产后处理流程,缺陷跟踪处理流程,缺陷跟踪的目的,缺陷管理工具
- VSCode插件:嵌套注释
猜你喜欢
Bert usage and word prediction based on Keras_bert model
MySQL (6)
Parameter introduction and selection points of wireless module

Arbitrum 专访 | L2 Summer, 脱颖而出的 Arbitrum 为开发者带来了什么?
第一学年课程期末考试

GCC Rust is approved to be included in the mainline code base, or will meet you in GCC 13

leetcode-1161:最大层内元素和

斩获BAT、TMD技术专家Offer,我都经历了什么?

软件测试报告有哪些内容?

手把手教你配置Jenkins自动化邮件通知
随机推荐
手把手教你配置Jenkins自动化邮件通知
初识C语言 -- 数组
uniapp使用第三方字体
Fiddler抓包模拟弱网络环境测试
Centos 7.9安装PostgreSQL14.4步骤
Shell 脚本循环遍历日志文件中的值进行求和并计算平均值,最大值和最小值
GCC Rust is approved to be included in the mainline code base, or will meet you in GCC 13
leetcode-399:除法求值
MySql的安装配置超详细教程与简单的建库建表方法
数字图像隐写术之卡方分布
Installation problem corresponding to tensorflow and GPU version
Charging effect simulation
leetcode-1161:最大层内元素和
Bert usage and word prediction based on Keras_bert model
C语言小程序 -- 常见经典练习题
keep-alive cache component
How to expose Prometheus metrics in go programs
【genius_platform软件平台开发】第七十四讲:window环境下的静态库和动态库的一些使用方法(VC环境)
Basic Parameters of RF Devices 1
VSCode Plugin: Nested Comments