Constructing expression binary tree with prefix expression

In the study of expression binary tree , There are many interesting ways to construct its expression binary tree , Among them, there are many common ways to build expression binary trees by using prefix expressions , But in a document I read , This paper introduces the concept of constructing its expression binary tree in a non recursive way , Although relatively more troublesome , But in its code implementation , Exploration is still very meaningful .

First infix expression to build expression binary tree ( Non recursive )

c Language implementation :

Prefix expression :*-23+45

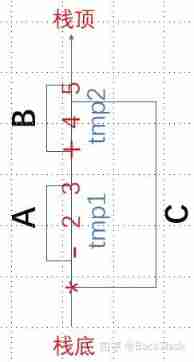
Pictured , If you read the prefix expression from left to right , Find the operator and put it on the stack , After finding the second operand of the operator , Organize them into the smallest subtree , Then the operator comes out of the stack , Continue to traverse the next character . In the process , Operands are not stacked , There are only operators in the stack , When the operators are organized into the smallest computing unit, they are pushed out of the stack . When the stack is empty , Note that the first infix expression is traversed .

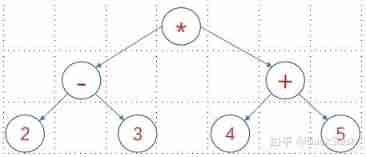
Combined with its expression binary tree graph to understand :
Prefix expression :*-23+45
Observe its expression and binary tree graph , Read from left to right , Is the preorder traversal of binary tree , We define a tree node pointer to record its path node .

Because what we want to build is a binary tree , So both numbers and operators are tree nodes , Each symbol read must be entered into the tree node , The stack also stores tree nodes .
First encounter operators on the stack , The pointer points to its left child node , Then continue to read
If you encounter numbers , Just save to the node data in , And determine whether the node symbol of the tree at the top of the stack has a right child node ,
If there is no right child node , Initialize its right child node , And the pointer points to its right child node ,
If the tree node at the top of the stack already has a right child node , Note that the symbol at the top of the stack has two numeric child nodes , This constitutes a basic formula unit , The node at the top of the stack leaves the stack ,
The pointer continues to point to the top element , And continue to determine whether the tree node symbol at the top of the stack has a right child node
Until the right child node at the top of the stack does not exist , Or its stack is empty .

Analyze the nodes in the stack :
1. There is a parent-child relationship between symbols , And only for the relationship between parents and left children ,
2. Its nodes must have left child nodes , There is a right child node , And after completing the assignment , It is necessary to perform the stack operation
3. The memory of the stack is the tree node , When the stack must save the tree node address , That is, the tree node pointer , Instead of variable values , Because when reading and storing the right child on the top node of the stack , Make sure that the tree nodes also change .

C Language :
Stack , Tree structure declaration :
.h

// Binary tree chain storage structure 
typedef struct node {
    
    char data;
    struct node* lchild, * rchild;
}BiTNode, *BiTree;

typedef BiTree  ElemType; 
// Here, the tree node must use a pointer , That is, the address is stored when the symbol node is stacked , It's not worth it 
// In this way, when modifying data for tree nodes in the stack , Only in this way can we have a real impact on the tree nodes 
typedef struct {
    
	ElemType data[MAXSIZE];
	int top;
}SqStack,* SqStackS;  // Order of the stack 

int InitStack(SqStackS* S);
int StackEmpty(SqStackS S);
int  Push(SqStackS S, ElemType x);
int Pop(SqStackS S);
int Pops(SqStackS S, ElemType* x);
int GetTop(SqStackS S, ElemType* x);

.c

#include "Stack_Tool.h"
#include<stdlib.h> // Dynamic distribution function and random function 

#include<stdio.h>// Input and output 
// Because malloc() function , It is <stdlib.h> The contents of the library , If it is not imported into the warehouse , You will not be able to dynamically allocate memory ,
// It will cause dynamic memory allocation failure , Variable < Unable to read memory >
int InitStack(SqStackS *S) {
    
	*S = (SqStackS)malloc(sizeof(SqStack));
    (*S)->top = -1;
	return 1;
}

int StackEmpty(SqStackS S) {
    
	if (S->top == -1)
		return 1;
	else
		return 0;
}

int  Push(SqStackS S, ElemType  x) {
    
	if (S->top == MAXSIZE - 1)
		return 0;
	S->data[++S->top] =x;  // Add one to the pointer first , Go back to the stack 
	return 1;
}
int Pop(SqStackS S) {
    
	if (S->top == -1)
		return 0;
	S->top--;
	return 1;
}
int Pops(SqStackS S, ElemType *x) {
    
	if (S->top == -1)
		return 0;
	*x = S->data[S->top--];  // First out of the stack , The pointer minus one more 
	return 1;

}
// Get the address of the top member of the stack , Get the stack address position through the stack pointer , Then return its member address through the secondary pointer 
// Here, because the pointer is stored in the stack , And although the pointer passes the address , But it is the pointer address of the tree node type 
// And we want to save the address of the pointer of the tree node , You need the type pointer of the tree node , That's the second level pointer 
int GetTop(SqStackS S, ElemType* x) {
    
	if (S->top == -1)
		return 0;
	*x = S->data[S->top];
	return 1;
}

 

main.c

char nextToken(char formula[]) {
    
	static int pos = 0;   //static pos Initialize only once , And continue to accumulate 
	     while (formula[pos] != '\0' && formula[pos] == ' ') {
     pos++; }// Skip spaces  
	     return formula[pos++]; 
}
int isOpNum(char ch) {
    
	if (ch == '+' || ch == '-' || ch == '*' || ch == '/'|| ch == '(' || ch == ')')
		return 1;
	else
		return 0;
}

void createTree(BiTree* bt,char formula[]) {
    
	
	char* c = formula;
	SqStackS parentStack;
	InitStack(&parentStack);

	*bt= (BiTree)malloc(sizeof(BiTNode));
	BiTree tpointer=*bt;

	char single = nextToken(c);
	while(single !='\0'){
    

		if (isOpNum(single)) {
        // If it's a character , Character stack , Point the pointer to its left child 
			tpointer->data = single;
			tpointer->lchild = (BiTree)malloc(sizeof(BiTNode));
			tpointer->rchild = NULL;
			// Into the stack 1, String stack pointer , Because the pointer saves the address , No changes to tree nodes , Use values to pass 
			Push(parentStack, tpointer);
			tpointer = tpointer->lchild;
		}
		else {
                   // If it's a number 
			tpointer->data = single;
			GetTop(parentStack, &tpointer);
			while (tpointer->rchild!=NULL){
    
				Pop(parentStack);
				if (StackEmpty(parentStack))
					return;
				GetTop(parentStack, &tpointer);
			}
			
			tpointer->rchild = (BiTree)malloc(sizeof(BiTNode));
			tpointer = tpointer->rchild;
		}

		single = nextToken(c);

	}

}

Output bracketed infix expression

// Output bracketed infix expression 
void BtreeToExp(BiTree btt, int deep) {
    
	if (btt == NULL)
		return;
	else if (isOpNum(btt->data)) {
    
		if (deep > 1)
			printf("(");
		BtreeToExp(btt->lchild, deep + 1);
		printf("%c", btt->data);
		BtreeToExp(btt->rchild, deep + 1);
		if (deep > 1)
			printf(")");
	}
	else {
    
		printf("%c", btt->data);
	}

}


void  BtreeToE(BiTree btt) {
    
	BtreeToExp(btt, 1);
}

Recursively operate on the expression binary tree

int  yunSuan(int a, int b, char data) {
    
	int count;
	switch (data) {
    
	case '+':
		count = a + b;
		break;
	case '-':
		count = a - b;
		break;
	case '*':
		count = a * b;
		break;
	case '/':
		count = a / b;
		break;
			
	}
	return count;
}
// Through the expression binary tree , Output the result of the operation 

int sum(BiTree btt) {
    
	int count;
	char data = btt->data;
	// If it's a sign 
	if (isOpNum(data)) {
     
		int a = sum(btt->lchild);
		int b = sum(btt->rchild);
		
		// Then call the operation method 
		//return  Calculation results ;
		count=yunSuan(a, b, data);
		return count;
	}
	count = data -48;
	// take char To int, Then return 
	return count;
}

main() function :

int main() {
    
	BiTree bt=NULL;
	char formula[20] ;
	printf(" Give me the preorder expression to build a binary tree ：\n");
	
	// Abreast of the times VS2019 Provided in scanf_s(). In the call , A number can be provided to indicate the maximum number of characters read .
	scanf_s("%s", &formula,20);
	createTree(&bt, formula);

	// Output bracketed infix expression 
	printf(" Infix expression is :");
	BtreeToE(bt);
	printf("\n");
	// After building the binary tree , Calculate the binary tree .
	// Through left and right recursion 
	int count=sum(bt);
	printf(" The result is :%d", count);
}

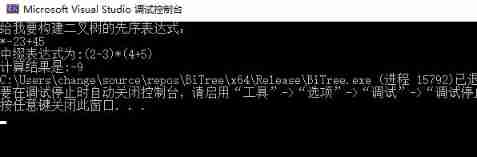
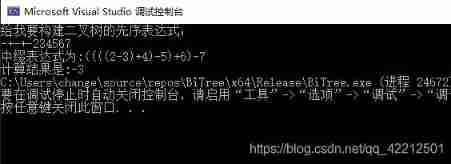
test :

Reference documents :
non-recursive algorithm
Tree and binary tree summary
Expression to build binary tree