当前位置:网站首页>NowCoderTOP35-40 - continuous update ing
NowCoderTOP35-40 - continuous update ing
2022-08-05 09:45:00 【Wang Hee Hee-】
TOP35. 判断是不是完全二叉树
public class Solution {
/** * 判断完全二叉树,当遍历当前层时如果遇到空节点,如果该空节点右侧还有节点,说明该树 * 一定不是完全二叉树,直接返回false,遍历完返回true * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param root TreeNode类 * @return bool布尔型 */
public boolean isCompleteTree (TreeNode root) {
// 空树是完全二叉树
if(root == null) return true;
// 辅助队列
Queue<TreeNode> queue = new LinkedList<>();
// 先将根节点入队
queue.offer(root);
// 标记空节点
boolean flag = true;
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
if(cur == null) {
// 如果遇到某个节点为空,进行标记
flag = false;
}else {
// 遇到空节点直接返回false
if(flag == false) return false;
queue.offer(cur.left);
queue.offer(cur.right);
}
}
return true;
}
}
TOP36. 判断是不是平衡二叉树
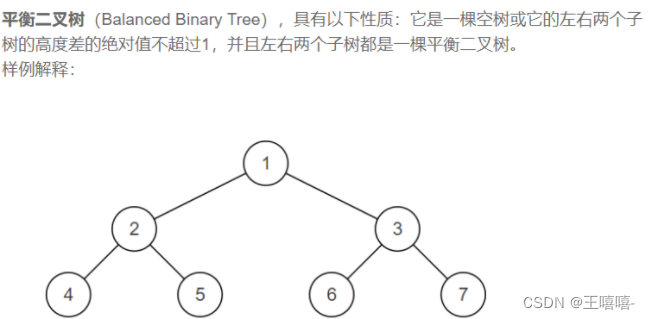
public class Solution {
public boolean IsBalanced_Solution(TreeNode root) {
if(root == null) return true;
// Check whether the left subtree and the right subtree conform to the rules,And the depth cannot exceed2
return IsBalanced_Solution(root.left) && IsBalanced_Solution(root.right)
&& Math.abs(TreeDepth(root.left) - TreeDepth(root.right)) <= 1;
}
// 二叉树的深度
public int TreeDepth(TreeNode root) {
if(root == null) return 0;
return Math.max(TreeDepth(root.left), TreeDepth(root.right)) + 1;
}
}
TOP37. 二叉搜索树的最近公共祖先
public class Solution {
/** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param root TreeNode类 * @param p int整型 * @param q int整型 * @return int整型 */
public int lowestCommonAncestor (TreeNode root, int p, int q) {
// 递归
// Empty trees have no recent common ancestor
if(root == null) return -1;
// pq在该节点两边说明这就是最近公共祖先
if(p >= root.val && q <= root.val || (q >= root.val && p <= root.val)){
return root.val;
}
//pq都在该节点的左边
else if(p <= root.val && q <= root.val) {
// 进入左子树
return lowestCommonAncestor(root.left, p , q);
}
else
// 进入右子树
return lowestCommonAncestor(root.right, p , q);
}
// 非递归
// // The path from the root node to both nodes
// ArrayList<Integer> listP = getPath(root, p);
// ArrayList<Integer> listQ = getPath(root, q);
// int res = 0;
// // 比较两个路径,找到第一个不同的点
// for(int i = 0; i < listP.size() && i < listQ.size(); i++) {
// int p1 = listP.get(i);
// int q1 = listQ.get(i);
// // 最后一个相同的节点就是最近公共祖先
// if(p1 == q1) res = p1;
// }
// return res;
// }
//
// // 求根节点到目标节点的路径
// public ArrayList<Integer> getPath(TreeNode root, int target) {
// ArrayList<Integer> list = new ArrayList<Integer>();
// TreeNode node = root;
// // 节点值不同,可以直接用值比较
// while(node.val != target) {
// list.add(node.val);
// if(target > node.val) node = node.right;
// else node = node.left;
// }
// // Add the node value to the linked list
// list.add(node.val);
// return list;
// }
}
TOP38. 在二叉树中找到两个节点的最近公共祖先
public class Solution {
public int lowestCommonAncestor (TreeNode root, int o1, int o2) {
// 递归法
if(root == null) return -1;
// When the node is a node of one of them
if(root.val == o1 || root.val == o2) return root.val;
// Find common ancestors in the left subtree
int l = lowestCommonAncestor(root.left, o1, o2);
// 右子树中寻找
int r = lowestCommonAncestor(root.right, o1, o2);
// 左子树中未找到
if(l == -1) return r;
// 右子树中未找到
if(r == -1) return l;
// Otherwise return the current node
return root.val;
}
// step 1:利用dfs求得根节点到两个目标节点的路径:每次选择二叉树的一棵子树往下找,同时路径数组增加这个遍历的节点值.
// step 2:一旦遍历到了叶子节点也没有,则回溯到父节点,寻找其他路径,回溯时要去掉数组中刚刚加入的元素.
// step 3:然后遍历两条路径数组,依次比较元素值.
// step 4:找到两条路径第一个不相同的节点即是最近公共祖先.
// ArrayList<Integer> path1 = new ArrayList<Integer>();
// ArrayList<Integer> path2 = new ArrayList<Integer>();
// // The path from the root node to both nodes
// dfs(root, path1, o1);
// // 重置标志位
// flag = false;
// // 查找下一个
// dfs(root, path2, o2);
// int res = 0;
// //比较两个路径,找到第一个不同的点
// for(int i = 0; i < path1.size() && i < path2.size(); i++) {
// int p1 = path1.get(i);
// int p2 = path2.get(i);
// if(p1 == p2) res = p1;
// else break;
// }
// return res;
// }
// // 记录是否找到到o的路径
// boolean flag = false;
// // 根节点到目标节点的路径
// public void dfs(TreeNode root, ArrayList<Integer> path, int o) {
// if(flag || root == null) return;
// // root node record
// path.add(root.val);
// // 节点值不同,soCan be compared by value
// if(root.val == o) {
// flag = true;
// return;
// }
// // dfs遍历
// dfs(root.left, path, o);
// dfs(root.right, path, o);
// // 找到
// if(flag) return;
// // 没有找到,回溯
// path.remove(path.size() - 1);
// }
}
TOP40. 重建二叉树
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] vin) {
int lenPre = pre.length;
int lenIn = vin.length;
// 边界
if(lenPre == 0 || lenIn == 0) return null;
// 构建根节点
TreeNode root = new TreeNode(pre[0]);
for(int i = 0; i < lenIn ; i++) {
// Find the preorder first element of the inorder traversal
if(pre[0] == vin[i]) {
// 构建左子树
// Arrays.copyOfRange 数组中指定范围copy from to(不包括to)
root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i + 1),
Arrays.copyOfRange(vin, 0, i));
//构建右子树
root.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i + 1, pre.length),
Arrays.copyOfRange(vin, i + 1, vin.length));
break;
}
}
return root;
}
}
边栏推荐
- 无题四
- 营销建议 | 您有一份八月营销月历待查收! 建议收藏 !
- PAT Class B-B1019 Digital Black Hole (20)
- CCVR eases heterogeneous federated learning based on classifier calibration
- matcher中find,matches,lookingAt匹配字符串的不同之处说明
- Science bosses say | Hong Kong rhubarb KaiBin teacher take you unlock the relationship between the matrix and 6 g
- Excuse me, guys, is it impossible to synchronize two databases in real time using Flink SQL CDC?
- 欧盟 | 地平线 2020 ENSEMBLE:D2.13 SOTIF Safety Concept(下)
- leetcode points to Offer 10- I. Fibonacci sequence
- C语言的高级用法
猜你喜欢

js 图形操作一(兼容pc、移动端实现 draggable属性 拖放效果)

Marketing Suggestions | You have an August marketing calendar to check! Suggest a collection!
IDEA performs the Test operation, resulting in duplicate data when data is inserted
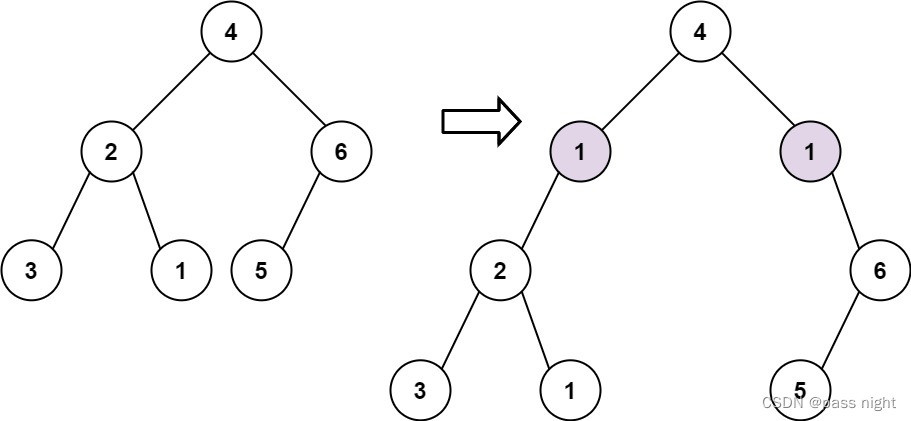
【LeetCode】623. Add a row to the binary tree

leetcode: 529. Minesweeper Game
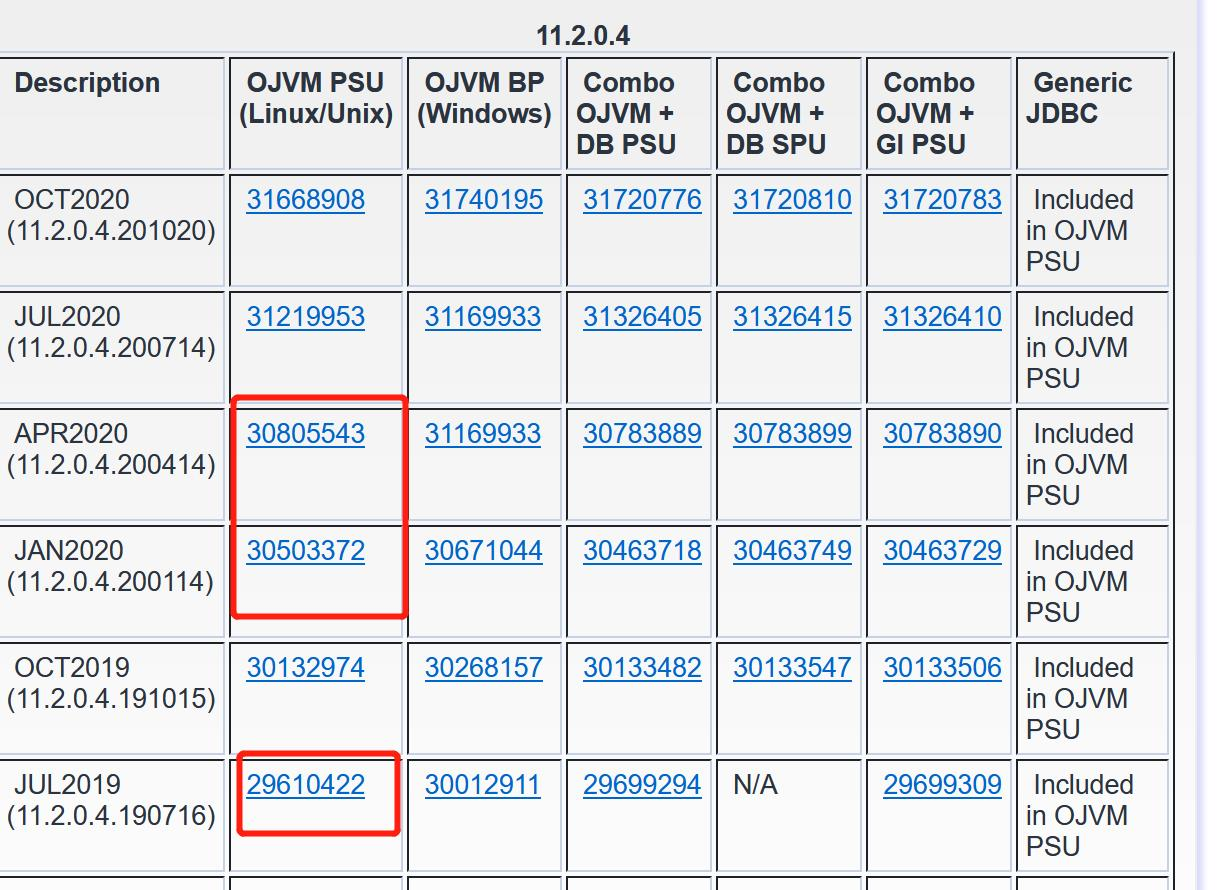
Which big guy has the 11G GI and ojvm patches in April or January 2020, please help?

seata源码解析:事务状态及全局锁的存储

七夕浪漫约会不加班,RPA机器人帮你搞定工作
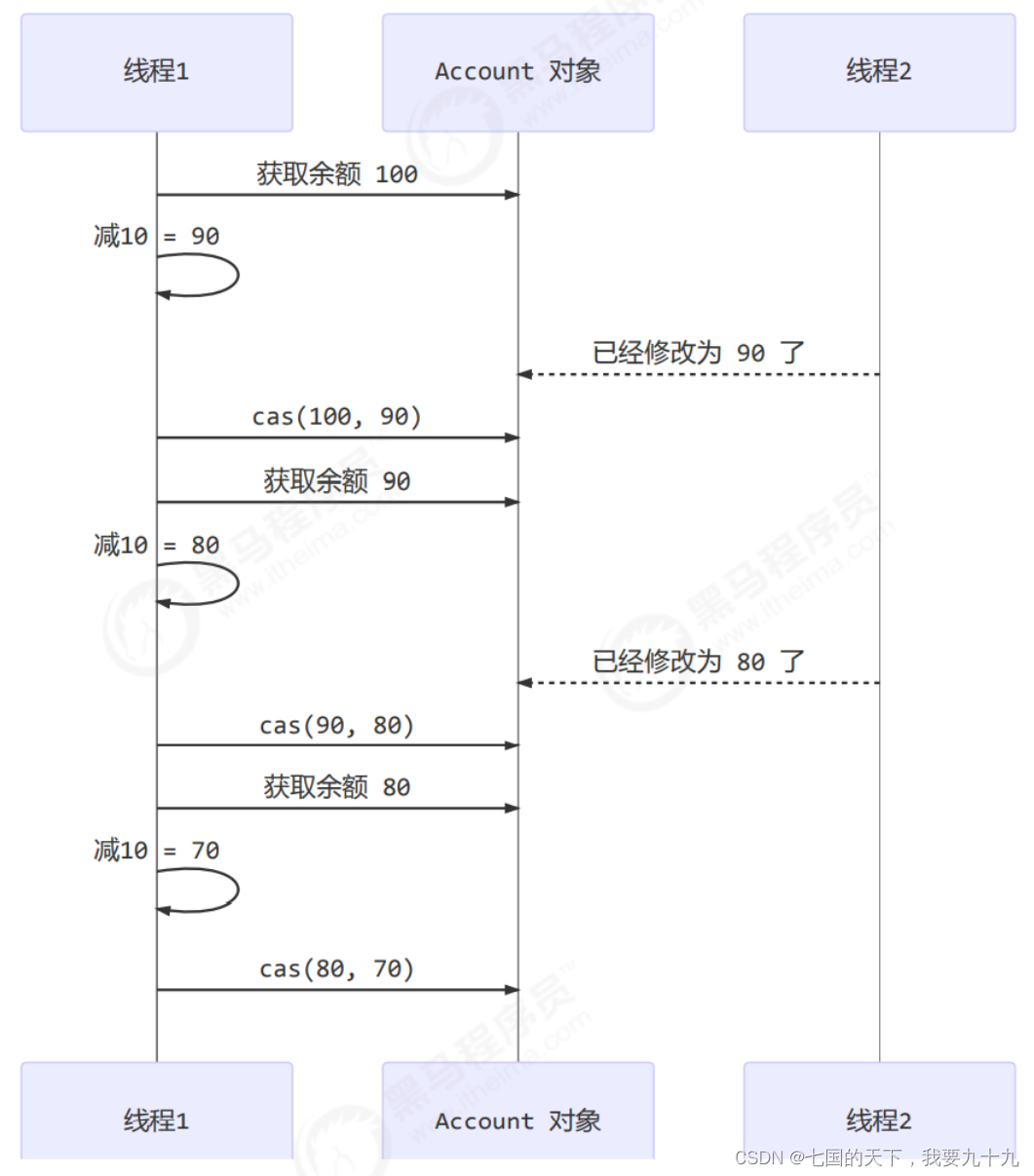
并发之CAS

Tanabata romantic date without overtime, RPA robot helps you get the job done
随机推荐
Jenkins使用手册(2) —— 软件配置
Qiu Jun, CEO of Eggplant Technology: Focus on users and make products that users really need
Neuron Newsletter 2022-07|新增非 A11 驱动、即将支持 OPC DA
19.服务器端会话技术Session
MySQL内部函数介绍
What is CRM Decision Analysis Management?
eKuiper Newsletter 2022-07|v1.6.0:Flow 编排 + 更好用的 SQL,轻松表达业务逻辑
【零基础玩转BLDC系列】无刷直流电机无位置传感器三段式启动法详细介绍及代码分享
Open Source Summer | How OpenHarmony Query Device Type (eTS)
无题八
js 图形操作一(兼容pc、移动端实现 draggable属性 拖放效果)
Can MySQL use aggregate functions without GROUP BY?
The difference between find, matches, lookingAt matching strings in matcher
After Keil upgrades to AC6, what changes?
Excuse me, guys, is it impossible to synchronize two databases in real time using Flink SQL CDC?
Overall design and implementation of Kubernetes-based microservice project
无题十一
IO流篇 -- 基于io流实现文件夹拷贝(拷贝子文件夹及子文件夹内文件)满满的干货
Seata source code analysis: initialization process of TM RM client
Assembly language (8) x86 inline assembly