当前位置:网站首页>图的最短路径的核心——松弛技术
图的最短路径的核心——松弛技术
2022-08-03 05:11:00 【二十八画之一】
写在前面
图的最短路径问题困扰了我很久,这两天接触到了松弛技术,突然找到了主线,所以写一下我对松弛技术的理解。内容主要是来自《算法导论》,但是大量的描述是离散数学的语言,但是我的离散实在是差劲,只能写写我现在的逻辑,但是正确性不能保证。
伪代码表示松弛技术
这是继承自《算法笔记》的写法,我觉得很简洁很准确,所以加一学习。
针对每一个图上的顶点,设置一个数组d[v],用来描述起点s到v的最短路径的上界,设置一个pre[v],用来标记前驱。
首先要进行初始化
INTIALIZE-SINGLE-SOURCE(G,s)
1 for each vertex v∈V[G]
2 do d[v]<--∞
3 pre[v],<--NIL
4 d[s]<--0
首先先解释,之后熟悉了就可以了。
<–是赋值、然后这个没有大括号,用缩进代表逻辑关系、形式写的像是函数,有函数和参数还有返回值、do是和for搭配。
这里的意思是对于每一个图上的顶点,d[v]赋值为无穷大,pre[v]赋值为NIL(意为无前驱),循环完成之后把d[s](起点)赋值为零。
之后是松弛技术
w(u,v)是指u到v的权值。
RELAX(u,v,w)
1 if d[v]>d[u]+w(u,v)
2 then d[v]<--d[u]+w(u,v)
3 pre[v]<--u
then是和if搭配。
感觉大道至简,不解释了。
关于松弛技术的定理
松弛技术看似简单,但是这些定理也是松弛技术的组成,他会回答为什么那些最短路径的算法是正确的,帮助我们理解,至于这些定理的证明有兴趣去看《算法导论》。这些定理我写的并不严谨,只是挑着对我之后推演有用的写,但保证是正确的。
m(u,v)意为u到为的最短路径
引理24.1 最短路径的子路径是最短路径
不解释
引理24.10 三角不等式
对于(u,v)的边来说m(s,v)<=m(s,u)+w(u,v)
引理24.11 上界性质
对任意v∈V,有d[v]>=m(s,v),而且在松弛技术的使用下(只用松弛技术改变d[v])一旦d[v]达到m(u,v)就不会改变了。
这里插一嘴,不严谨的考虑,因为松弛技术只会把d[v]变小,所以当d[v]最小自然不会变。
推论24.11 无路径性质
如果从s到v不存在路径,则总是有d[v]=m(s,v)= ∞。
引理24.14 收敛性质
如果s~>u–>v(s到v要经过u,而且u是v的前驱)是图G某u、v∈V的最短路径,而且在松弛边(u,v)之前的任何时间d[u]=m(s,u),则操作过后总有d[v]=m(u,v)。
这个引理是非常有用而且暧昧的,这里有一个大的前提需要说一下,就是u一定是v的前驱。所以这个必须成立。
引理24.15 路径松弛性质
如果p=<v0,v1,……,vk>是从s=v0到vk的最短路径,而且p的边按照(v0,v1)(v1,v2),……,(vk-1,vk)的顺序进行松弛,那么d[vk]=m(s,vk)。这个性质的保持并不受其他松弛操作的影响,即使他们与p边上的松弛操作混在一起也是一样的。
这个定理简直是重中之重了,之后的三个最短路径的写法都是对这个定理的一个执行。
这里隐含一个大前提,在没有负回路的情形下,一定存在 一个p是最短的,这个前提如此合理以至于我一直忽略。有这个序列只要按照这个序列连起来就是最短路径。
对松弛技术的收获
只要按照客观存在的最短路径按顺序去准备就可以完成最短路径的寻找。这是之后理解最短路径算法的核心逻辑。
进一步的说明一下,只要我们的最短路径的算法,依次准备出(s,v1),(v1,v2),…(vk-1,vk)就可以一步步实现最短。大多数的改动也只需要在松弛技术的代码里改动就行,毕竟其他的是走一个过场。而且是什么决定了这种准备逻辑呢?就是松弛技术的操作本身。
边栏推荐
猜你喜欢
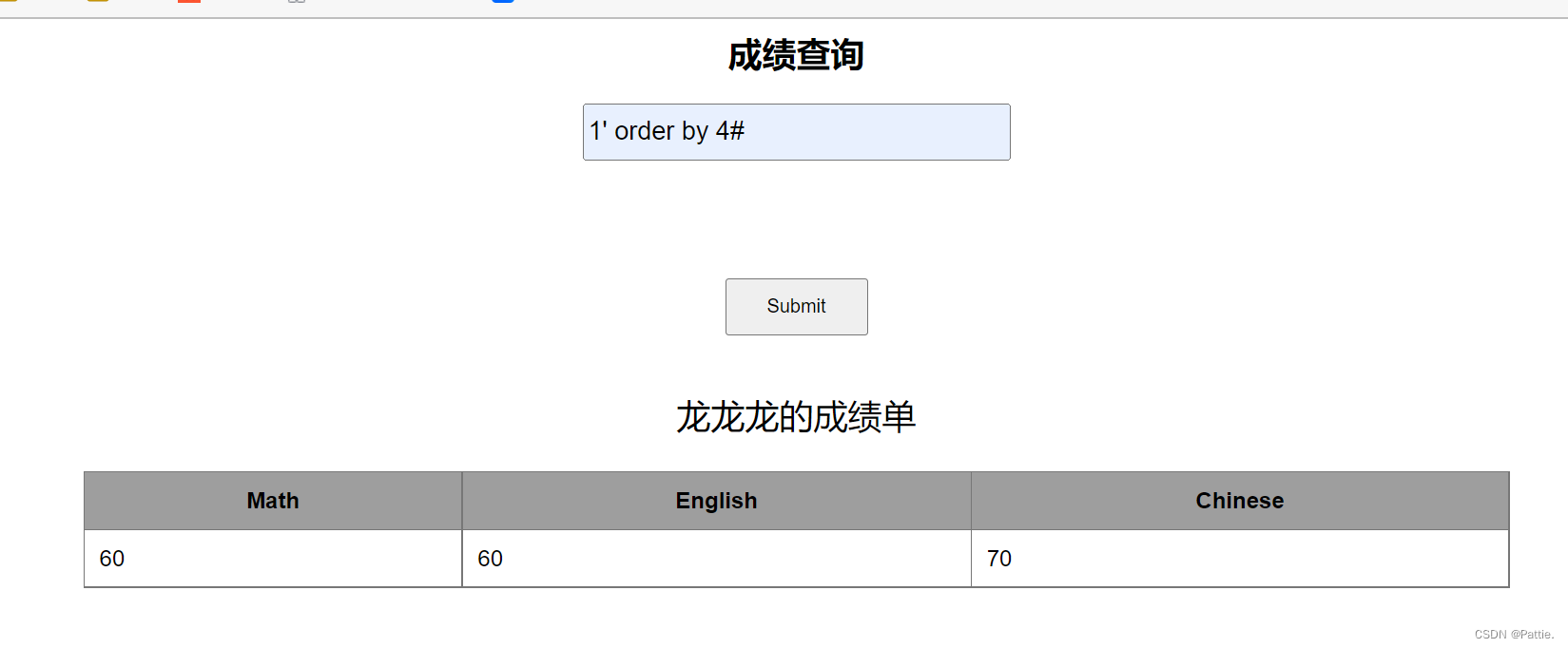
web安全-sql注入漏洞
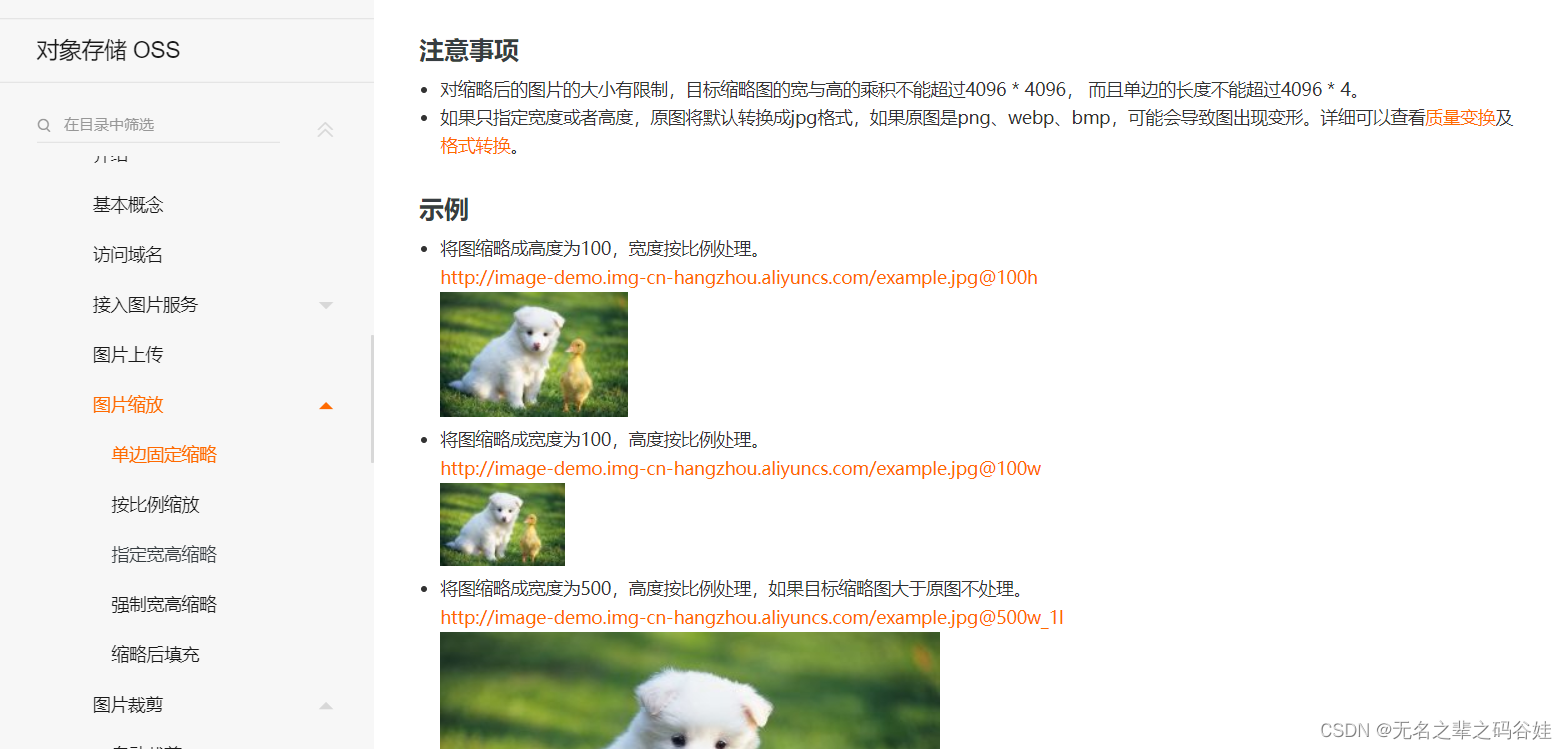
Ali cloud object storage oss private barrels to generate links

13.
lt.647. Palindromic substring + lt.516. Longest palindrome subsequence 
Build your own web page on raspberry pie (1)
Install IIS services (Internet Information Services (Internet Information Services, abbreviated IIS, Internet Information Services)
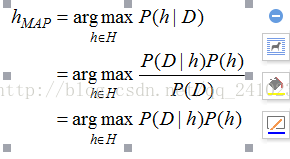
【转】最小描述长度准则MDL(Minimun Description Length)

Installation of Apache DolphinScheduler version 2.0.5 distributed cluster

曲线特征----曲线弯曲程度的探究

第三次HarmonyOS培训
用C语言来实现扫雷小游戏
随机推荐
dataframe插入一列
Pr第三次培训笔记
Makefile 遍历子目录模板
uni-app 滚动到顶部/指定位置
1. 两数之和
1094 谷歌的招聘 (20 分)
PotPlayer实现上班摸鱼电视自由
celery工作原理图
嵌入式-I2C-物理电路图
ss-2.子项目互相访问(order80 -> payment8001)
集合框架知识
7.21[日常]
Presto installation and deployment tutorial
-最高分-
Go (一) 基础部分2 -- if条件判断,for循环语句
【按位取反,逻辑操作符,条件操作符,逗号表达式,下标引用,函数调用,结构体】操作符后续+表达式求值(上)
7.18(7)
13.
lt.647. Palindromic substring + lt.516. Longest palindrome subsequence 生活原则。
lintcode2330 · 计算x秒后的时间