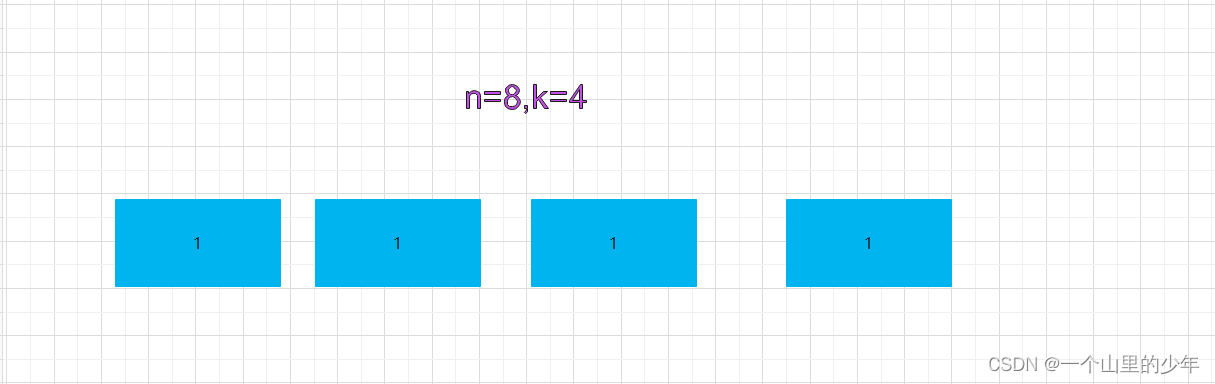当前位置:网站首页>数的划分之动态规划
数的划分之动态规划
2022-08-04 04:53:00 【一个山里的少年】
1.对应OJ链接:
2.题目描述:
3.解题思路:
方法一:直接暴力递归
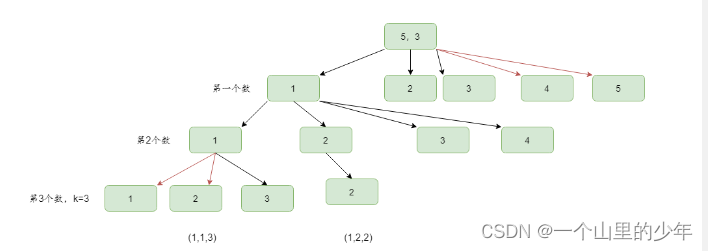
从index位置开始进行尝试一直到n,具体请看代码。
对应代码:
class Solution { public: /** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * * * @param n int 被划分的数 * @param k int 化成k份 * @return int */ int divideNumber(int n, int k) { // write code here return process(n, k, 1); } //递归含义:从index位置开始将n划分成k分的方法数 int process(int n, int k, int index) { if (k < 0) { return 0; } //如果剩下了0分那么只有当k为0时有一种划分结果 if (k == 0) { return n == 0 ? 1 : 0; } int ways = 0; for (int i = index; i <= n; i++) { //尝试i位置上的数 ways += process(n - i, k - 1, i); } return ways; } };
但是很不幸的是这种方法即使改成记忆化搜索和dp依然会超时。下面我们来看下面一种方法。感觉特别的妙:
我们可以将k想象成有k个盒子按照题目的意思就是每个盒子不能为空,那么我们可以提前给每个盒子都放入一个1这样一来盒子就不会是空的了。然后我们再将剩下的n-k个小球再放到k个盒子里面即可,此时就有多种可能性了 n-k个小球可以放到第一个盒子中,可以放到1和2这两个盒子当中也可以放到1到3这三个盒子当中,也可以放到1到k这些盒子当中。
对应代码:
class Solution { public: /** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * * * @param n int 被划分的数 * @param k int 化成k份 * @return int */ vector<vector<int>>dp; int mod=1000000000+7; int divideNumber(int n, int k) { // write code here // dp.resize(n+1,vector<vector<int>>(k+1,vector<int>(n+1,-1))); dp.resize(n+1,vector<int>(k+1,-1)); return process(n,k); } //将n划分成k分的方法数 int process(int n,int k) { if(n==k){ return 1; } if(k>n){ return 0; } if(dp[n][k]!=-1){ return dp[n][k]; } int ways=0; //剩下的n-k个小球放到k个盒子里面的可能性进行枚举 for(int i=1;i<=k;i++){ ways=(ways+process(n-k,i))%mod; } dp[n][k]=ways; return ways; } };
斜率优化:
对应代码:
class Solution { public: /** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * * * @param n int 被划分的数 * @param k int 化成k份 * @return int */ vector<vector<int>>dp; int mod=1000000000+7; int divideNumber(int n, int k) { // write code here // dp.resize(n+1,vector<vector<int>>(k+1,vector<int>(n+1,-1))); dp.resize(n+1,vector<int>(k+1,-1)); return process(n,k); } //将n划分成k分的方法数 int process(int n,int k) { if(k==0){ return n==0?1:0; } if(k==n){ return 1; } if(k>n){ return 0; } if(dp[n][k]!=-1){ return dp[n][k]; } int ways=process(n-1,k-1); ways=(ways+process(n-k,k))%mod; dp[n][k]=ways; return ways; } };
边栏推荐
- 2022 software test interview questions The latest ByteDance 50 real interview questions, 15k have been won after brushing, with explanation + Q&A
- 2022年软件测试——精选金融银行面试真题
- Large chain best freight d audit with what software?What are the functions?
- el-Select 选择器 底部固定
- 【id类型和NSObject指针 ObjectIve-C中】
- Towards Real-Time Multi-Object Tracking(JDE)
- mysql索引笔记
- [Skill] Using Sentinel to achieve priority processing of requests
- go module的介绍与应用
- 42. 接雨水
猜你喜欢
Mini program + e-commerce, fun new retail
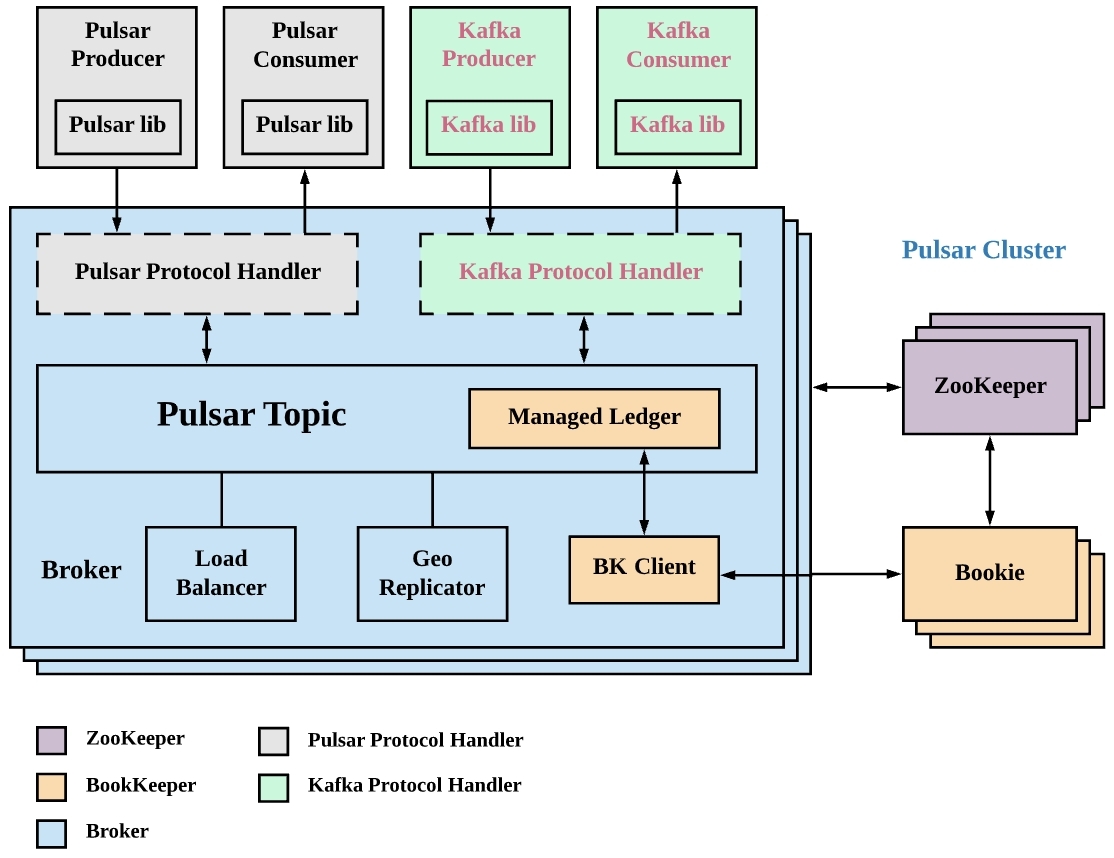
技术解析|如何将 Pulsar 数据快速且无缝接入 Apache Doris

你以为border-radius只是圆角吗?【各种角度】
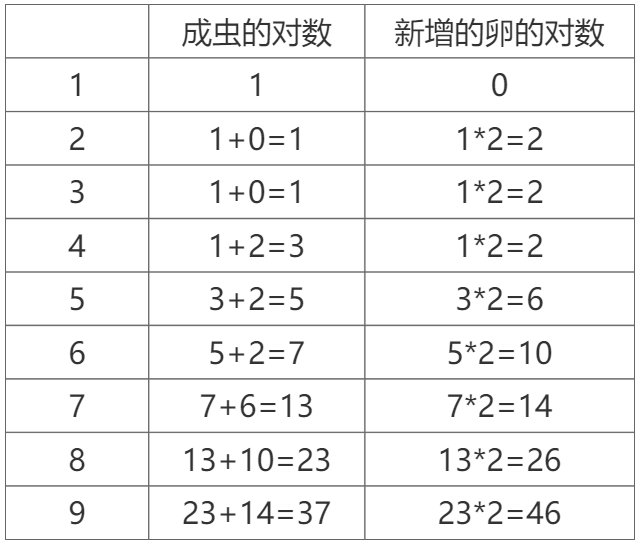
信息学奥赛一本通 1312:【例3.4】昆虫繁殖
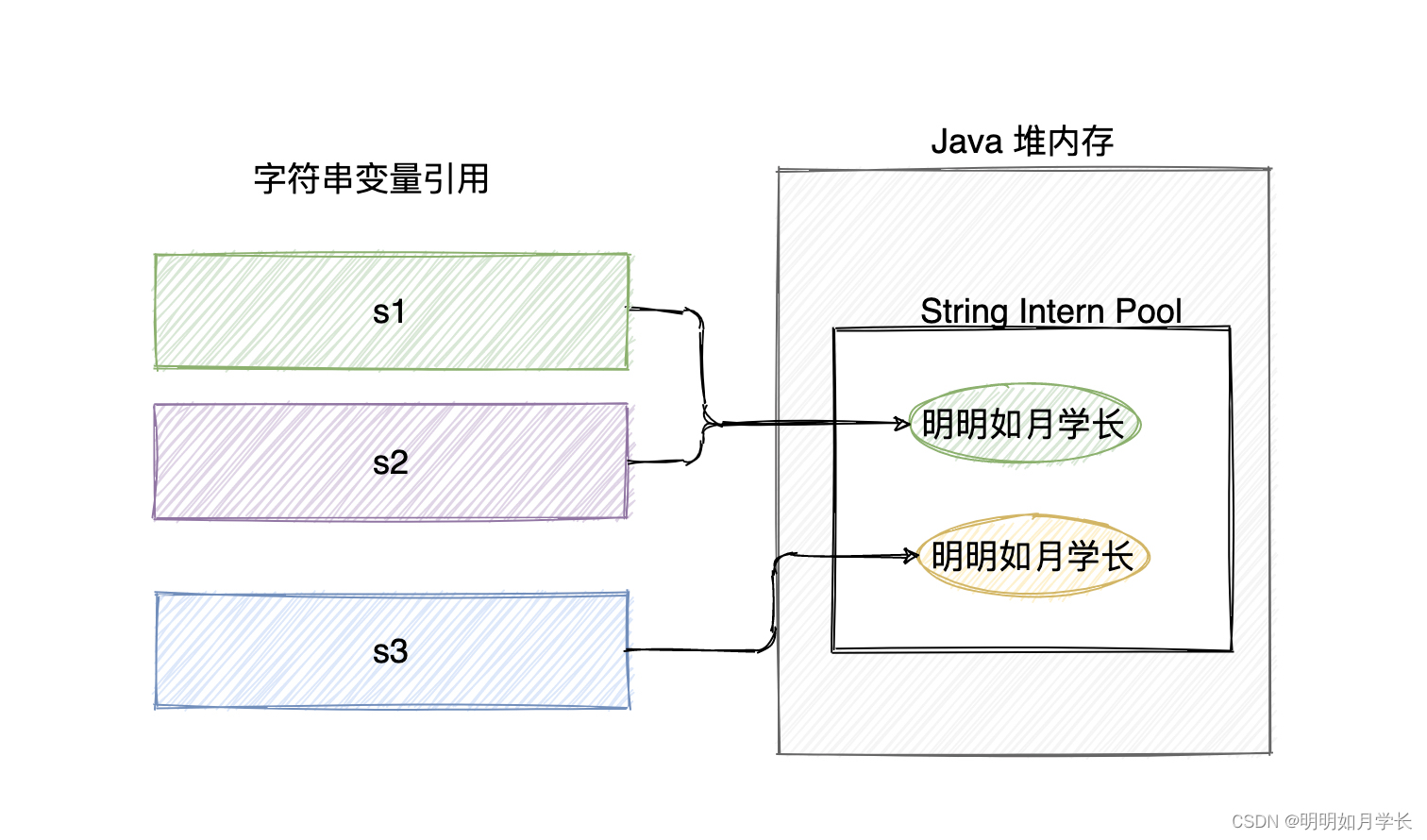
震惊,99.9% 的同学没有真正理解字符串的不可变性
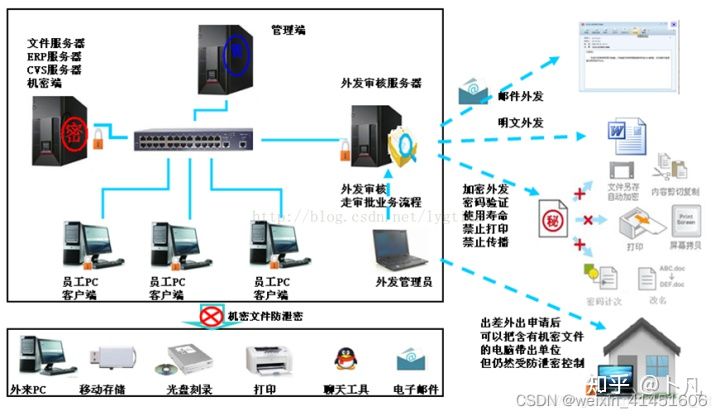
烧录场景下开发如何进行源代码保密工作
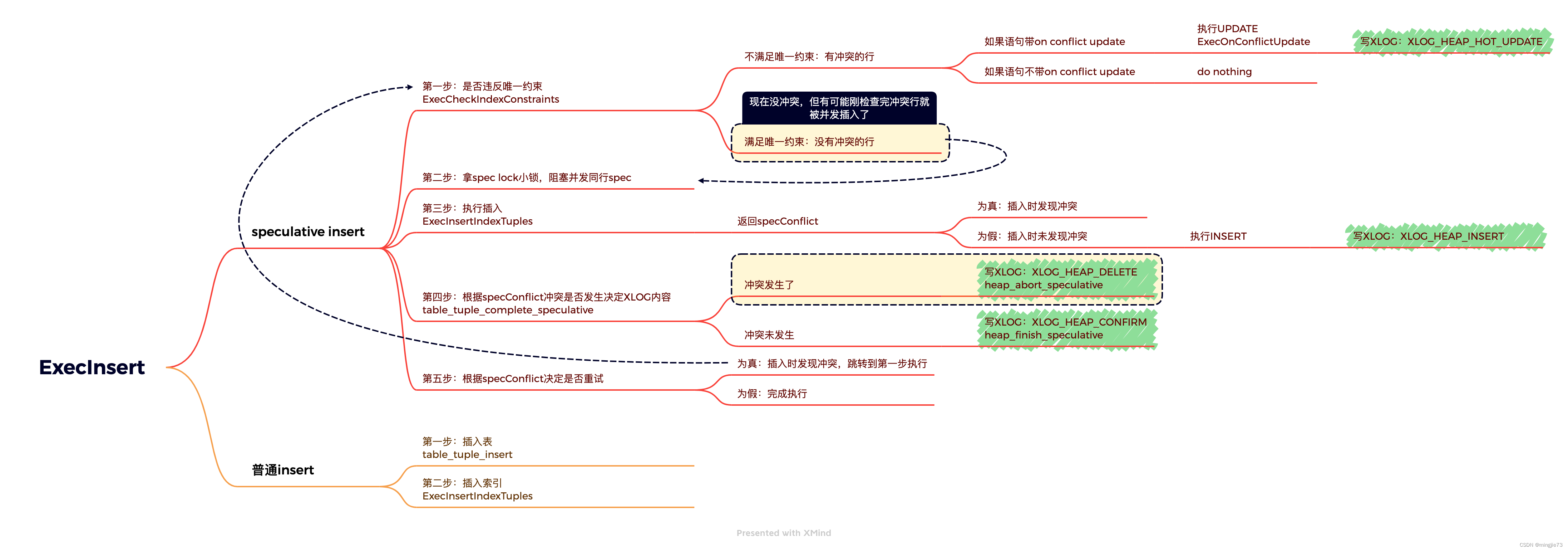
Postgresql source code (66) insert on conflict grammar introduction and kernel execution process analysis
Basic characteristics of TL431 and oscillator circuit

深度学习21天——卷积神经网络(CNN):实现mnist手写数字识别(第1天)
Simple operation of the file system
随机推荐
About yolo7 and gpu
C Expert Programming Chapter 4 The Shocking Fact: Arrays and Pointers Are Not the Same 4.3 What is a Declaration and What is a Definition
Hangdian Multi-School-Slipper- (tree map conversion + virtual point mapping)
如何动态添加script依赖的脚本
7. The principle description of LVS load balancing cluster
【21天学习挑战赛】图像的旋转问题(二维数组)
redis中常见的面试题
DataTable uses Linq for grouping and summarization, and converts the Linq result set into DataTable
系统设计.秒杀系统
8.Haproxy 搭建Web集群
[SemiDrive source code analysis] [MailBox inter-core communication] 47 - Analysis of RPMSG_IPCC_RPC mode limit size of single transmission and limit bandwidth test
share总结
Eight guiding principles to help businesses achieve digital transformation success
2023年PMP考试会用新版教材吗?回复来了!
Explain detailed explanation and practice
See how DevExpress enriches chart styles and how it empowers fund companies to innovate their business
7-3 LVS+Keepalived集群叙述与部署
大型连锁百货运维审计用什么软件好?有哪些功能?
3000 words, is take you understand machine learning!
day13--postman接口测试