当前位置:网站首页>Binary tree [full solution] (C language)
Binary tree [full solution] (C language)
2022-08-05 00:44:00 【Obto-】
目录:
--->>Basic information about binary trees
--->>二叉树的概念
--->>二叉树的性质
--->>构建二叉树
--->>二叉树的遍历
--->>二叉树的深度
--->>查找值为x的节点
--->>第kHow many elements the layer has
--->>叶子结点个数
--->>树的大小(元素总个数)
--->>TOP-K问题
--------------------------------------------------------------------------------------------------------------------------------
前言:This blog provides an overview of various operations on binary trees,Hope it will be helpful to the students who are studying,也希望大家多多指教
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-===-=-=-=-=-=-=-=-=-=-=-=-=---=-=-=-=-=-=-=-=-=-=-=
Basic information about binary trees
1.二叉树是一种重要的非线性数据结构,直观地看,它是数据元素(在树中称为结点)按分支关系组织起来的结构,很象自然界中的树那样
2.二叉树is an ordinal number with at most two characters per node,Usually the root of the subtree is called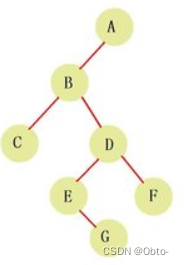 作 "左子树" 和"右子树":如图中‘C’为左子树‘D’为右子树
作 "左子树" 和"右子树":如图中‘C’为左子树‘D’为右子树
二叉树的概念
1.The nodes of a binary tree are a finite set
①要么 该集合为空
②要么 The set consists of a root node plus two binary trees called left and right subtrees
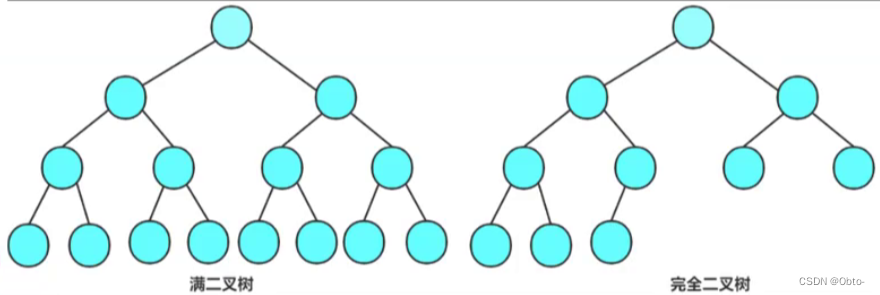
2.完全二叉树:完全二叉树是一种效率很高的数据结构,完全二叉树是由满二叉树引出来的
3.A full binary tree has all nodes两个子结点,A complete binary tree is a leaf node连续的 ,There can be no breaks in the middle
二叉树的性质
1.If the root node is specified as 1,则一颗非空二叉树的第 i 层上最多有2^(i-1).
2.If the root node is specified as 1,则深度为h的二叉树的最大节点数是2^h-1
3.对任何一颗二叉树;如果度为0的叶结点个数为n0,度为2的分支结点个数为n2则n0=n2+1
4.If the root node is specified as 1,具有nnodes are full of the depth of the binary tree h=log2(n+1)
5.Calculates the relationship between subscripted parent and child leftchildren = parent*2+1 rightchildren = parent*2+2 parent=(child-1)/2
构建二叉树
1.定义二叉树的结构
typedef int HPDataType;
typedef struct {
int data;
struct BTNode* left;
struct BTNode* right;
}BTNode;2.A function to create a node
BTNode* BuyNode(int x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
assert(node);
node->data = x;
node->left = node->right = NULL;
return node;
}3.linked binary tree
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;二叉树的遍历
前序遍历:
The traversal order is to visit the root node first and then visit the left node,Finally visit the right node
void Preorder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
printf("%d ", root->data);
Preorder(root->left);
Preorder(root->right);
}中序遍历:
The traversal order is to visit the left node first and then the root node,Finally visit the right node
void Preorder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
Preorder(root->left);
printf("%d ", root->data);
Preorder(root->right);
}后序遍历:
The traversal order is to visit the left node first and then the right node,最后访问根结点
void Preorder(BTNode* root)
{
if (root == NULL)
{
printf("# ");
return;
}
Preorder(root->left);
Preorder(root->right);
printf("%d ", root->data);
}层序遍历:
void LevelOrder(BTNode* root)
{
Queue q; //Define a queue name calledq
QueueInit(&q); //初始化队列
if (root)
{
QueuePush(&q,root); //Top the number into the queue
}
while (!QueueEmpty(&q)) //当队列为空时结束循环
{
BTNode* front = QueueFront(&q);//Save the tree top pointer
printf("%d ", front->data);
QueuePop(&q); //出队头
if (front->left != NULL) //入左子树
{
QueuePush(&q, front->left);
}
if (front->right != NULL) //入右子树
{
QueuePush(&q, front->right);
}
}
printf("\n");
QueueDestory(&q); //队列的销毁
}二叉树的深度
int TreeDepth(BTNode* node)
{
if (node == NULL)
return 0;
if (TreeDepth(node->left) > TreeDepth(node->right))
return TreeDepth(node->left) + 1;
else
return TreeDepth(node->right) + 1;
}查找值为x的节点
BTNode* TreeFind(BTNode* node, int x)
{
if (node == NULL)
return;
if (node->data == x)
return node;
TreeFind(node->left,x);
TreeFind(node->right,x);
return NULL;
}第kHow many elements the layer has
int TreeKLevel(BTNode* node , int k)
{
if (node == NULL)
return 0;
if (k == 1)
return 1;
return TreeKLevel(node->left, k - 1) + TreeKLevel(node->right, k - 1) ;
}叶子结点个数
int TreeLeafSize(BTNode* node)
{
if (node == NULL)
return 0;
if (node->left == NULL && node->right == NULL)
{
return 1;
}
return TreeLeafSize(node->left) + TreeLeafSize(node->right);
}树的大小(元素总个数)
int TreeSize(BTNode* node)
{
if (node == NULL)
return 0;
else {
return TreeSize(node->left) + TreeSize(node->right) + 1;
}
}TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大
比如:世界500强,国服前200
对于TOP-K问题,The easiest and most straightforward way is to sort,但是如果数据量特别大,Sorting is impossible,最佳的方式就是用堆来解决
Then there is a problem,If kept in the heapkThe number is the smallest in the total data,At this time, it is necessary to insert and merge into the heapt调整
①向上调整
void AdjustUp(HPDataType * a,int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] < a[parent])
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}②向下调整
void AdjustDown(HPDataType* a, int size, int parent)
{
int child = parent * 2 + 1;
while (child < size)
{
if (child + 1 < size && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}TOP-K的实现代码
void PrintTopk(int *a,int n,int k)
{
int* heap = (int*)malloc(sizeof(int) * k);
//先将前kdata import array
for (int i = 0; i < k; i++)
{
heap[i] = a[i];
}
//将k个数据建堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)//The last row of the binary tree does not need to be adjusted downwards
{
AdjustDown(heap, k, i);
}
/*for (int i = 1; i < k; i++)
{
AdjustUp(heap, i);
}*/
for (int j = k; j < n; j++)
{
if (a[j] > heap[0])
{
heap[0] = a[j];
AdjustDown(heap, k, 0);
}
}
for (int i = 0; i < k; i++)
printf("%d ", heap[i]);
}边栏推荐
- 倒计时1天!8月2日—4日与你聊聊开源与就业那些事!
- Software testing interview questions: the difference and connection between black box testing, white box testing, and unit testing, integration testing, system testing, and acceptance testing?
- D - I Hate Non-integer Number (count of selected number dp
- 机器学习(公式推导与代码实现)--sklearn机器学习库
- 软件测试面试题:BIOS, Fat, IDE, Sata, SCSI, Ntfs windows NT?
- gorm联表查询-实战
- 国内网站用香港服务器会被封吗?
- 软件测试面试题:测试用例通常包括那些内容?
- 2022 Multi-school Second Session K Question Link with Bracket Sequence I
- Redis visual management software Redis Desktop Manager2022
猜你喜欢
随机推荐
After the staged testing is complete, have you performed defect analysis?
3. pcie.v 文件
2022杭电多校训练第三场 1009 Package Delivery
leetcode: 266. All Palindromic Permutations
软件测试面试题:BIOS, Fat, IDE, Sata, SCSI, Ntfs windows NT?
Opencv——视频跳帧处理
二叉树[全解](C语言)
进程间通信和线程间通信
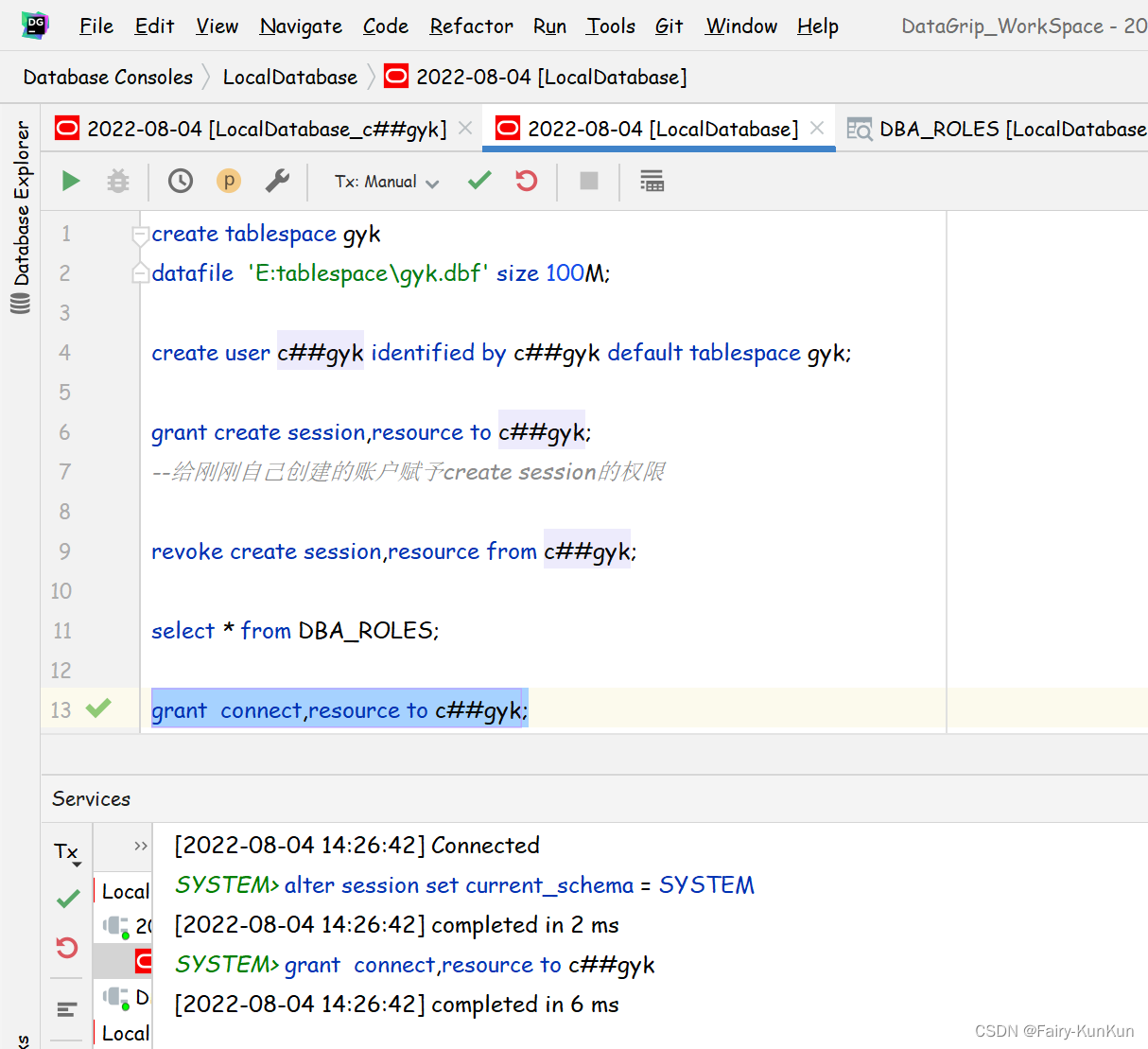
oracle创建表空间
tiup update
关于我仔细检查审核过关于工作人员页面,返回一个所属行业问题
创意代码表白
MBps与Mbps区别
"WEB Security Penetration Testing" (28) Burp Collaborator-dnslog out-band technology
tiup status
Software testing interview questions: What stages should a complete set of tests consist of?
canvas 高斯模糊效果
EL定时刷新页面中的皕杰报表实例
tiup telemetry
[idea] idea configures sql formatting
![[FreeRTOS] FreeRTOS and stm32 built-in stack occupancy](/img/33/3177b4c3de34d4920d741fed7526ee.png)