当前位置:网站首页>Notes on numerical analysis (II): numerical solution of linear equations
Notes on numerical analysis (II): numerical solution of linear equations
2022-07-03 09:19:00 【fishfuck】
direct method
Catch up method
The coefficient matrix is tridiagonal matrix
A = [ b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ⋱ ⋱ ⋱ a n − 1 b n − 1 c n − 1 a n b n ] A= \begin{bmatrix} b_1 & c_1 \\ a_2 & b_2 & c_2\\ & a_3 &b_3 &c_3 \\ & & \ddots & \ddots &\ddots \\ & & & a_{n-1} &b_{n-1} & c_{n-1}\\ &&&& a_n & b_n \end{bmatrix} A=⎣⎢⎢⎢⎢⎢⎢⎡b1a2c1b2a3c2b3⋱c3⋱an−1⋱bn−1ancn−1bn⎦⎥⎥⎥⎥⎥⎥⎤
The equations of
{ b 1 x 1 + c 1 x 2 = f 1 a i x i − 1 + b i x i + c i x i + 1 = f i , i = 2 , 3 , 4 , ⋯ , n − 1 a n x n − 1 + b n x n = f n \left\{ \begin{array}{lr} b_1x_1+c_1x_2=f_1\\ a_ix_{i-1}+b_ix_i+c_ix_{i+1}=f_i,&i=2, 3,4,\cdots,{n-1}\\ a_nx_{n-1}+b_nx_n=f_n \end{array} \right. ⎩⎨⎧b1x1+c1x2=f1aixi−1+bixi+cixi+1=fi,anxn−1+bnxn=fni=2,3,4,⋯,n−1
, The solution of the catch-up method is divided into two steps :
Elimination process
Process the given tridiagonal equations into unit upper didiagonal equations
{ x i + u i x i + 1 = y i , i = 1 , 2 , 3 , 4 , ⋯ , n − 1 x n = y n \left\{ \begin{array}{lr} x_i + u_ix_{i+1}=y_i,&i=1,2, 3,4,\cdots,{n-1}\\ x_n = y_n \end{array} \right. { xi+uixi+1=yi,xn=yni=1,2,3,4,⋯,n−1
, The processing procedure is
{ u 1 = c 1 b 1 , y 1 = f 1 b 1 u i = c i ( b i − a i u i − 1 ) , i = 2 , 3 , 4 , ⋯ , n − 1 y i = f i − a i y i − 1 b i − a i u i − 1 , i = 2 , 3 , 4 , ⋯ , n \left\{ \begin{array}{lr} u_1=\frac {c_1}{b_1},y_1=\frac {f_1}{b_1}\\ u_i=\frac{c_i}{(b_i-a_iu_{i-1})},&i=2, 3,4,\cdots,{n-1}\\ y_i=\frac{f_i-a_iy_{i-1}}{b_i-a_iu_{i-1}},&i=2, 3,4,\cdots,{n} \end{array} \right. ⎩⎪⎨⎪⎧u1=b1c1,y1=b1f1ui=(bi−aiui−1)ci,yi=bi−aiui−1fi−aiyi−1,i=2,3,4,⋯,n−1i=2,3,4,⋯,n
The process of retrogression
{ x n = y n x i = y i − u i x i + 1 , i = 1 , 2 , 3 , 4 , ⋯ , n − 1 \left\{ \begin{array}{lr} x_n = y_n\\ x_i =y_i- u_ix_{i+1},&i=1,2, 3,4,\cdots,{n-1} \end{array} \right. { xn=ynxi=yi−uixi+1,i=1,2,3,4,⋯,n−1
Be careful , Only when tridiagonal matrix satisfies Diagonally dominant when , The meet
{ ∣ b 1 ∣ > ∣ c 1 ∣ ∣ b i ∣ > ∣ a i ∣ + ∣ c 1 ∣ , i = 1 , 2 , 3 , 4 , ⋯ , n − 1 ∣ b n ∣ > ∣ a n ∣ \left\{ \begin{array}{lr} |b_1|>|c_1|\\ |b_i|>|a_i|+|c_1|,&i=1,2, 3,4,\cdots,{n-1}\\ |b_n|>|a_n| \end{array} \right. ⎩⎨⎧∣b1∣>∣c1∣∣bi∣>∣ai∣+∣c1∣,∣bn∣>∣an∣i=1,2,3,4,⋯,n−1
The catch-up process will not be interrupted .
Tridiagonal matrix L U LU LU decompose
Is there any method that can directly start from the coefficient matrix of tridiagonal equations Direct processing How to find out the system of didiagonal equations on the unit ? We consider the matrix L U LU LU decompose .
[ b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ⋱ ⋱ ⋱ a n − 1 b n − 1 c n − 1 a n b n ] = [ d 1 l 2 d 2 l 3 d 3 ⋱ ⋱ l n d n ] [ 1 u 1 1 u 2 ⋱ ⋱ 1 u n − 1 1 ] \begin{bmatrix} b_1 & c_1 \\ a_2 & b_2 & c_2\\ & a_3 &b_3 &c_3 \\ & & \ddots & \ddots &\ddots \\ & & & a_{n-1} &b_{n-1} & c_{n-1}\\ &&&& a_n & b_n \end{bmatrix} =\begin{bmatrix} d_1 & \\ l_2 & d_2 &\\ & l_3 &d_3 & \\ & & \ddots & \ddots & \\ &&& l_n & d_n \end{bmatrix} \begin{bmatrix} 1 & u_1 \\ & 1 &u_2\\ & & \ddots & \ddots & \\ &&& 1 & u_{n-1}\\ &&&&1 \end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎡b1a2c1b2a3c2b3⋱c3⋱an−1⋱bn−1ancn−1bn⎦⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡d1l2d2l3d3⋱⋱lndn⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡1u11u2⋱⋱1un−11⎦⎥⎥⎥⎥⎤
among
L = [ d 1 l 2 d 2 l 3 d 3 ⋱ ⋱ l n d n ] , U = [ 1 u 1 1 u 2 ⋱ ⋱ 1 u n − 1 1 ] L=\begin{bmatrix} d_1 & \\ l_2 & d_2 &\\ & l_3 &d_3 & \\ & & \ddots & \ddots & \\ &&& l_n & d_n \end{bmatrix}, U=\begin{bmatrix} 1 & u_1 \\ & 1 &u_2\\ & & \ddots & \ddots & \\ &&& 1 & u_{n-1}\\ &&&&1 \end{bmatrix} L=⎣⎢⎢⎢⎢⎡d1l2d2l3d3⋱⋱lndn⎦⎥⎥⎥⎥⎤,U=⎣⎢⎢⎢⎢⎡1u11u2⋱⋱1un−11⎦⎥⎥⎥⎥⎤
,
And l i = a i l_i=a_i li=ai. It's not hard to find out , U U U Matrix is the coefficient matrix of the system of two diagonal equations on the unit we need .
How do we get U U U Array ? consider L L L and U U U Matrix multiplication of , The equations can be obtained { b 1 = d 1 c i = u i d i , i = 1 , 2 , 3 , 4 , ⋯ , n − 1 b i + 1 = u i a i + 1 + d i + 1 , \left\{ \begin{array}{lr} b_1=d_1\\ c_i=u_id_i,&i=1,2, 3,4,\cdots,{n-1}\\ b_{i+1}=u_ia_{i+1}+d_{i+1}, \end{array} \right. ⎩⎨⎧b1=d1ci=uidi,bi+1=uiai+1+di+1,i=1,2,3,4,⋯,n−1
So we can Line by line Determine the matrix L L L and U U U The elements of , Its calculation formula is { d 1 = b 1 u i = c i d i , i = 1 , 2 , 3 , 4 , ⋯ , n − 1 d i + 1 = b i + 1 − u i a i + 1 , \left\{ \begin{array}{lr} d_1=b_1\\ u_i=\frac {c_i}{d_i},&i=1,2, 3,4,\cdots,{n-1}\\ d_{i+1}=b_{i+1}-u_ia_{i+1}, \end{array} \right. ⎩⎨⎧d1=b1ui=dici,di+1=bi+1−uiai+1,i=1,2,3,4,⋯,n−1
solve A x = f Ax=f Ax=f It can be equivalent to solving L ( U x ) = f L(Ux)=f L(Ux)=f, That is, it is equivalent to solving L y = f Ly=f Ly=f and U x = y Ux=y Ux=y Two equations .
about L y = f Ly=f Ly=f, It is the lower two diagonal equations , The specific form is { d 1 y 1 = f 1 a i y i − 1 + d i y i = f i , i = 2 , 3 , 4 , ⋯ , n \left\{ \begin{array}{lr} d_1y_1=f_1\\ a_iy_{i-1}+d_iy_i=f_i,&i=2, 3,4,\cdots,{n} \end{array} \right. { d1y1=f1aiyi−1+diyi=fi,i=2,3,4,⋯,n
Huidai , have to { y 1 = f 1 d 1 y i = f i − a i y i − 1 d i , i = 2 , 3 , 4 , ⋯ , n \left\{ \begin{array}{lr} y_1=\frac{f_1}{d_1}\\ y_i=\frac{f_i-a_iy_{i-1}}{d_i},&i=2, 3,4,\cdots,{n} \end{array} \right. { y1=d1f1yi=difi−aiyi−1,i=2,3,4,⋯,n
about U x = y Ux=y Ux=y, It is the system of two diagonal equations on the unit , The solution can be obtained by using the back substitution process in the catch-up method .
边栏推荐
- Internet Protocol learning record
- 【点云处理之论文狂读经典版11】—— Mining Point Cloud Local Structures by Kernel Correlation and Graph Pooling
- 【点云处理之论文狂读前沿版8】—— Pointview-GCN: 3D Shape Classification With Multi-View Point Clouds
- Principles of computer composition - cache, connection mapping, learning experience
- Wonderful review | i/o extended 2022 activity dry goods sharing
- 【点云处理之论文狂读前沿版13】—— GAPNet: Graph Attention based Point Neural Network for Exploiting Local Feature
- Solve POM in idea Comment top line problem in XML file
- 教育信息化步入2.0,看看JNPF如何帮助教师减负,提高效率?
- 【点云处理之论文狂读前沿版12】—— Adaptive Graph Convolution for Point Cloud Analysis
- 推荐一个 yyds 的低代码开源项目
猜你喜欢

LeetCode 513. Find the value in the lower left corner of the tree

拯救剧荒,程序员最爱看的高分美剧TOP10
On a un nom en commun, maître XX.
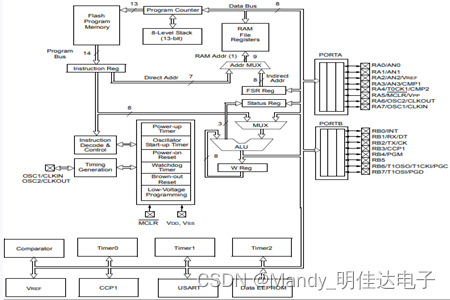
Pic16f648a-e/ss PIC16 8-bit microcontroller, 7KB (4kx14)

PIC16F648A-E/SS PIC16 8位 微控制器,7KB(4Kx14)

On February 14, 2022, learn the imitation Niuke project - develop the registration function

数字化管理中台+低代码,JNPF开启企业数字化转型的新引擎

Data mining 2021-4-27 class notes
![[point cloud processing paper crazy reading cutting-edge version 12] - adaptive graph revolution for point cloud analysis](/img/c6/5f723d9021cf684dcfb662ed3acaec.png)
[point cloud processing paper crazy reading cutting-edge version 12] - adaptive graph revolution for point cloud analysis

Beego learning - Tencent cloud upload pictures
随机推荐
Build a solo blog from scratch
推荐一个 yyds 的低代码开源项目
Education informatization has stepped into 2.0. How can jnpf help teachers reduce their burden and improve efficiency?
Internet Protocol learning record
Beego learning - Tencent cloud upload pictures
Banner - Summary of closed group meeting
dried food! What problems will the intelligent management of retail industry encounter? It is enough to understand this article
[point cloud processing paper crazy reading classic version 13] - adaptive graph revolutionary neural networks
[set theory] order relation (eight special elements in partial order relation | ① maximum element | ② minimum element | ③ maximum element | ④ minimum element | ⑤ upper bound | ⑥ lower bound | ⑦ minimu
Hudi 集成 Spark 数据分析示例(含代码流程与测试结果)
AcWing 787. 归并排序(模板)
Methods of checking ports according to processes and checking processes according to ports
Severity code description the project file line prohibits the display of status error c2440 "initialization": unable to convert from "const char [31]" to "char *"
Jenkins learning (II) -- setting up Chinese
[point cloud processing paper crazy reading classic version 8] - o-cnn: octree based revolutionary neural networks for 3D shape analysis
2022-2-14 learning xiangniuke project - Session Management
Basic knowledge of network security
Recommend a low code open source project of yyds
【点云处理之论文狂读经典版13】—— Adaptive Graph Convolutional Neural Networks
Sword finger offer II 091 Paint the house