当前位置:网站首页>石子 无限拿
石子 无限拿
2022-08-04 12:36:00 【EdwinAze】
石子 无限拿
给定 n 堆石子,两位玩家轮流操作,每次操作可以从任意一堆石子中拿走任意数量的石子(可以拿完,但不能不拿),最后无法进行操作的人视为失败。
问如果两人都采用最优策略,先手是否必胜。
思路
若为 2, 3堆, 先手在3堆里拿1个, 为 2 2。
之后只要跟后手拿的数量相同, 后手一定失败。
定理:
a 1 ∧ a 2 ∧ a 3 . . . ∧ a n = 0 先手必败 a_{1} \wedge a_{2} \wedge a_{3}...\wedge a_{n}= 0 先手必败 a1∧a2∧a3...∧an=0先手必败
证明:
0 ∧ 0 ∧ 0 ∧ 0... ∧ 0 = 0 a 1 ∧ a 2 ∧ a 3 . . . ∧ a n ≠ 0 \begin{align*} 0\wedge0\wedge0\wedge0...\wedge0 = 0\\ a_{1} \wedge a_{2} \wedge a_{3}...\wedge a_{n} \not= 0 \\ & \end{align*} 0∧0∧0∧0...∧0=0a1∧a2∧a3...∧an=0
不等于0时, 设结果为 x x x
x x x 的二进制表示为 10100100 10100100 10100100
a i a_i ai的二进制表示 1100100110 1100100110 1100100110
一定存在 a i a_i ai 在 x x x 最高位 k k k 位上为1。
则 a i ∧ x < a i a_{i} \wedge x < a_i ai∧x<ai , 那么就拿走 少的那一部分。
此时 a i = a i ∧ x a_{i}= a_{i} \wedge x ai=ai∧x 带入到原来式子后得到:
x ∧ x = 0 x \wedge x = 0 x∧x=0
故先手必赢。
等于0时, 设同样可以拿走一些, 剩下 a i ′ a_i' ai′个
a 1 ∧ a 2 ∧ a 3 . . . a i ∧ . . ∧ a n = 0 a 1 ∧ a 2 ∧ a 3 . . . a i ′ ∧ . . ∧ a n = 0 式子相异或得 a i ∧ a i ′ = 0 a i = a i ′ \begin{align*} a_{1} \wedge a_{2} \wedge a_{3}. ..a_{i}\wedge..\wedge a_{n} = 0\\ a_{1} \wedge a_{2} \wedge a_{3}. ..a_{i}'\wedge..\wedge a_{n} = 0\\ 式子相异或得 \\ a_{i}\wedge a_{i}' = 0 \\ a_{i} = a_{i}' \end{align*} a1∧a2∧a3...ai∧..∧an=0a1∧a2∧a3...ai′∧..∧an=0式子相异或得ai∧ai′=0ai=ai′
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int readInt()
{
int t ;
scanf("%d", &t);
return t;
}
int n;
int main()
{
int x;
cin >> n;
cin >> x;
n -= 1;
while(n--)
x ^= readInt();
if(x) cout << "Yes\n";
else cout << "No\n";
}
边栏推荐
猜你喜欢

Why is Luo Zhenyu's A-share dream so difficult to fulfill?
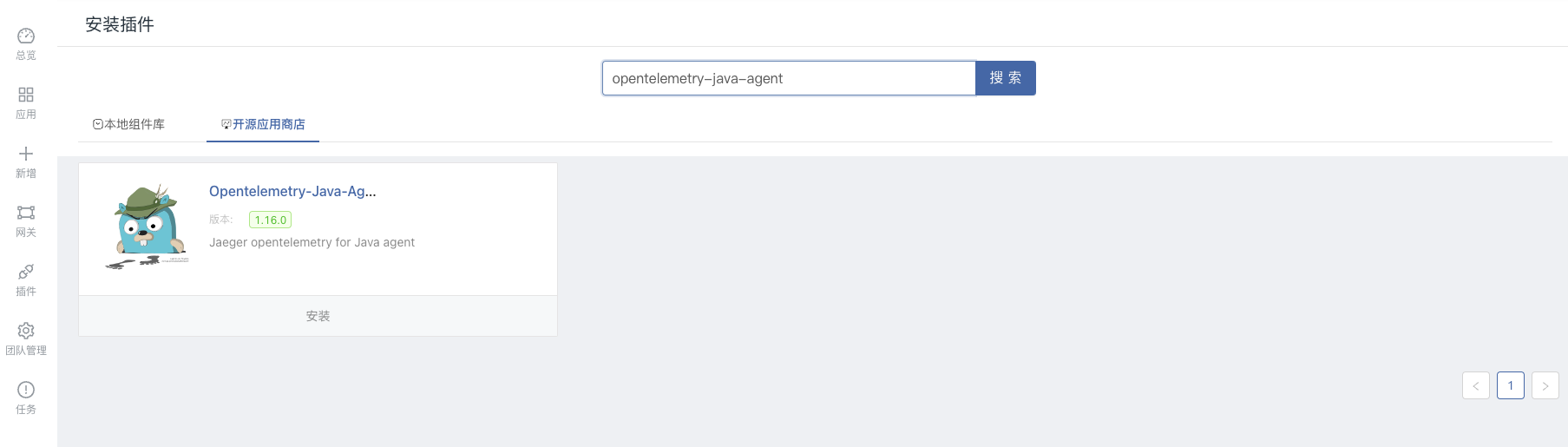
Practical sharing of distributed link tracking Jaeger + microservice Pig on Rainbond
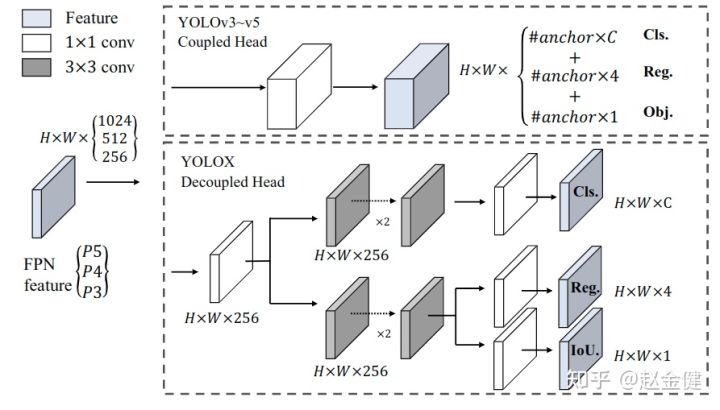
yolo系列的head模块
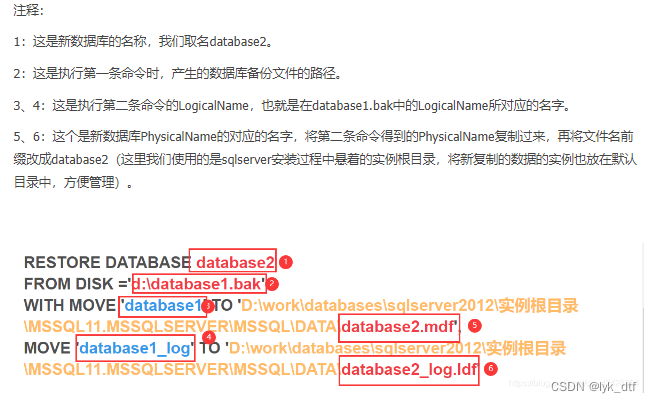
使用SQLServer复制数据库

分布式链路追踪Jaeger + 微服务Pig在Rainbond上的实践分享
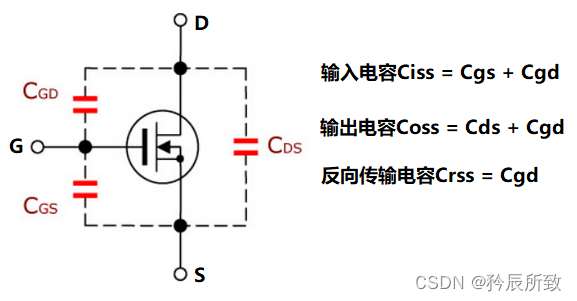
A comprehensive understanding of MOS tubes, an article is enough

Neck modules of the yolo series
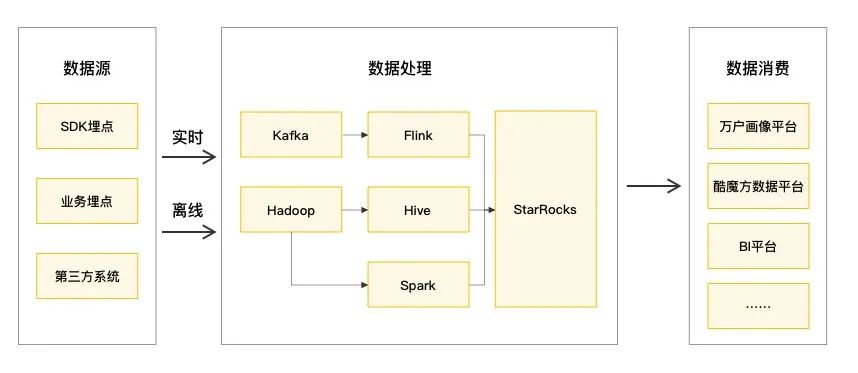
酷开科技 × StarRocks:统一 OLAP 分析引擎,全面打造数字化的 OTT 模式
树莓派入门
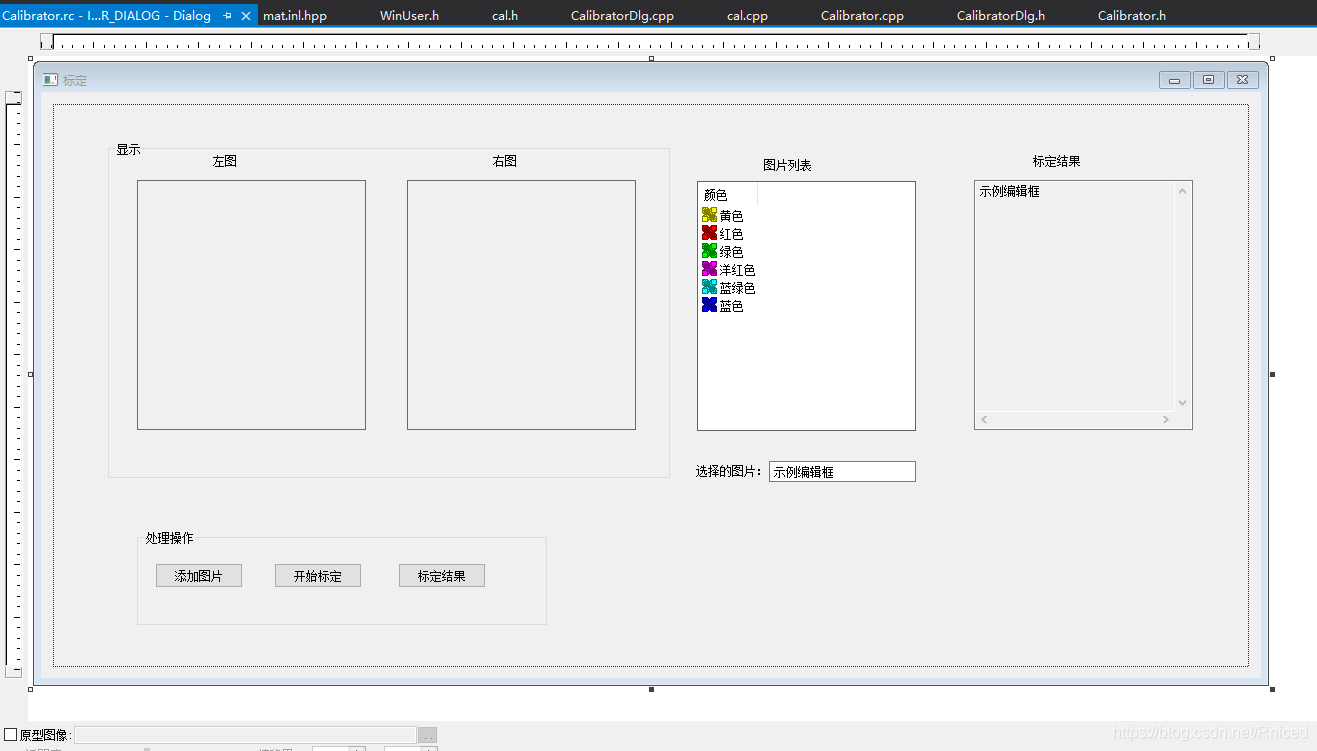
MFC的相机双目标定界面设计
随机推荐
动规(16)-并查集基础题——亲戚(Relations)
接入华为游戏防沉迷,点击防沉迷弹窗后游戏闪退
使用COLMAP初步三维重建
yolo系列的head模块
MySQL必知必会(初级篇)
为什么密码云服务平台是云时代的必然之选?
数据中台建设(九):数据中台资产运营机制
分布式链路追踪Jaeger + 微服务Pig在Rainbond上的实践分享
Chinese valentine's day of young people crazy to make money, earn 140000 a week
“蔚来杯“2022牛客暑期多校训练营3 C
WPF---Grid布局讲解
Nacos手摸手教学【二】Nacos注册中心
移动跨端技术方案分析对比
ShanDong Multi-University Training #4 A、B、C、G
LeetCode Daily Question (858. Mirror Reflection)
倒计时 3 天|一起看云原生 Meetup 的六大议题
Access Huawei game anti-addiction, click the anti-addiction pop-up window, the game crashes
Linux-Docker-Mysql安装
大神们都在用的神器,你和大神只差一个它!!
Control CD-ROM with VbScript