当前位置:网站首页>基于交替迭代法的交直流混合系统潮流计算matlab程序iEEE9节点系统算例
基于交替迭代法的交直流混合系统潮流计算matlab程序iEEE9节点系统算例
2022-07-31 06:02:00 【电磁MATLAB】
基于交替迭代法的交直流混合系统潮流计算matlab程序iEEE9节点系统算例
参考文献:
由于受端负荷量持续增大,直流输电受端系统的电压稳定性能自然引起了人们的关注。目前,交直流混合电网的电压稳定分析大致分为两类,即静态电压稳定分析和动态电压稳定分析,本聚焦于前者。传统分析中,有效短路比评价交直流电网的强度,VSI指标评价受端电网电压稳定性,但两者均未能揭示受端电网电压失稳的机理。
1 交直流系统的等值模型
如图所示为交直流系统等值的示意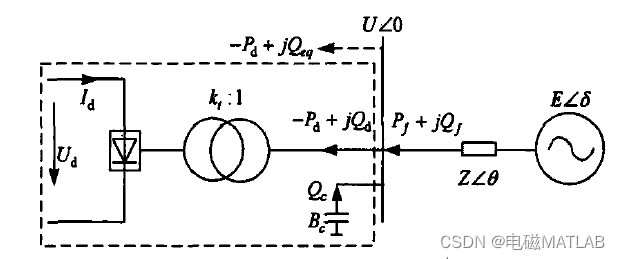
其基本特性方程可表示为式
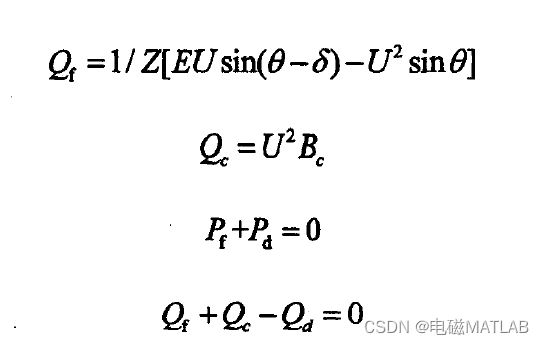

1.1 整流器定电流逆变器定电压(CC-CU)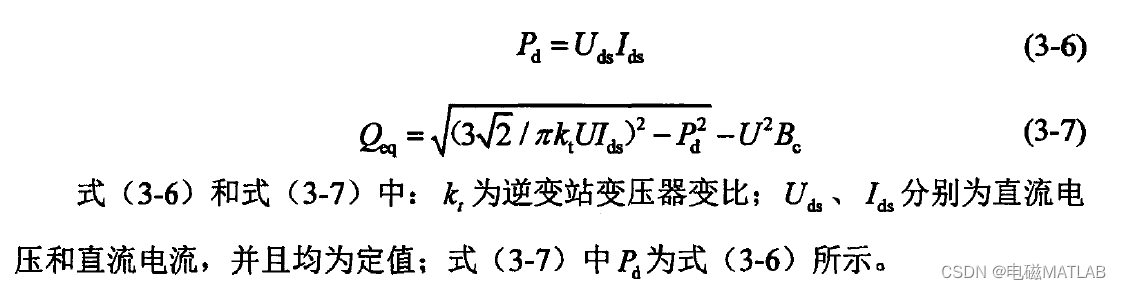
1.2 整流器定电流逆变器定关断角(CC-CIA)
1.3 整流器定功率逆变器定电压(CP-CU)
1.4 整流器定功率逆变器定关断角(CP-CIA)
2 iEEE9节点系统算例
7与8节点改为直流支路。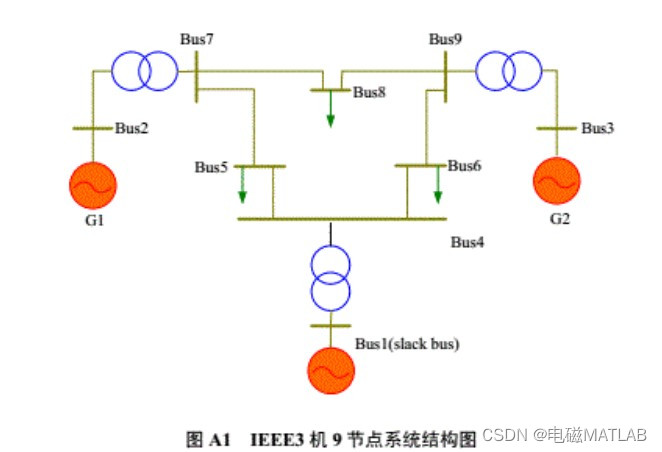
3 matlab程序运行结果
4 matlab程序
1)主函数
//基于交替迭代法的交直流混合系统潮流计算matlab程序iEEE9节点系统算例
%% 5种控制模式,直流未知数为UD ID SD PD QD Contrl_ang 参考王云鹏文章附件控制方式
%function flow_calculation
clear;
clc;
close all
tic
eval('case9')
T=0.00001;
%% 参数
kk=1;%迭代次数
line=size(Line.con,1);%支路数目
n=max(Bus.con(:,1));%找出第1,2列的最大值,即节点数
TT=ones(n,1)*T;%收敛误差设置
%% 创建导纳矩阵Y
Y=zeros(n);%创建导纳矩阵Y
U=ones(n,1);
dU=zeros(n,1);
U(PV.con(:,1))=PV.con(:,5);
U(SW.con(:,1))=SW.con(:,4);
th=zeros(n,1);
dth=zeros(n,1);
Pg=zeros(n,1);
Pl=zeros(n,1);
Ql=zeros(n,1);
Qg=zeros(n,1);
Pg(PV.con(:,1))=PV.con(:,4);
Pl(PQ.con(:,1))=PQ.con(:,4);
Ql(PQ.con(:,1))=PQ.con(:,5);
%% 计算导纳矩阵
for m=1:line
a=Line.con(m,1);%首节点a
b=Line.con(m,2);%末节点b
z=Line.con(m,8)+1i*Line.con(m,9);%节点ab间的阻抗
y2=1i*Line.con(m,10)/2;%导纳/2
if real(z)==0
k=Line.con(m,7)*Bus.con(b,2)/Bus.con(a,2);%变比K
else
k=1;
end
Y(a,b)=-1/k/z;%ab间互导纳
Y(b,a)=Y(a,b);
Y(a,a)=Y(a,a)+y2+(k-1)/(k*z)+1/k/z;%求自导纳
Y(b,b)=Y(b,b)+y2+(1-k)/k^2/z+1/k/z;
% C(a)=data(m,7);%输入节点a,b的补偿电容导纳
% C(b)=data(m,8);
end
%将节点导纳的实虚部分开
B=imag(Y);
G=real(Y);
%判断PQ、PV、平衡节点的个数
PQn=size(PQ.con,1);
PVn=size(PV.con,1);
SWn=size(SW.con,1);
%% 直流节点编号
DCn=Hvdc.con(:,[1 2])';%直流节点编号
ACn=setdiff(1:n,union(DCn,SW.con(1,1)))';
Ndc=size(DCn,1);%直流节点个数
Nac=size(ACn,1);%交流节点个数
pn=setdiff(1:n,SW.con(1,1))';
qn=setdiff(pn,PV.con(:,1));
Pn=intersect(ACn, pn);%交流节点P方程节点
Qn=intersect(ACn, qn);%交流节点Q方程节点
p=size(Pn,1); %交流节点P方程个数
q=size(Qn,1); %交流节点Q方程个数
% YK=zeros(p+q);
DPa=zeros(p,1);
DQa=zeros(q,1);
DPt=zeros(Ndc,1);
DQt=zeros(Ndc,1);
Dd1=zeros(Ndc,1);
Dd2=zeros(Ndc,1);
Dd3=zeros(Ndc,1);
Dd4=zeros(Ndc,1);
Dd5=zeros(1,1);
H=zeros(p+Ndc);
N=zeros(p+Ndc,q+Ndc);
M=zeros(q+Ndc,p+Ndc);
L=zeros(q+Ndc);
JRX=zeros(9,9);
%% 直流迭代初值设置+控制方式
Vd=ones(Ndc,1)*1.1562;%直流电压初值
Id=0.5;
% fai=ones(Ndc,1)*30/180*pi;%功率因数角初值30°
Pd=0.6.*ones(Ndc,1);
Qd=0.3.*ones(Ndc,1);
Sd=0.5.*ones(Ndc,1);
Control_ang=[20/180*pi;17/180*pi];%换流器控制角,第一个为alpha,第二个为gama
% Control_ang(2)=30/180*pi;
W=cos(Control_ang);
Kt=ones(Ndc,1);%直流支路两端变压器变比值设置
%% 直流参数设置
% ku=0.995;%换相效应常数,王锡凡181页
Rdc=0.0625;%直流电阻
Xc=[0.1345;0.1257];%整流及逆变侧变压器电抗,写入真实值
disp('请输入控制方式:')
disp('方式1:整流侧定电流,逆变侧定电压')
disp('方式2:整流侧定电流,逆变侧定熄弧角')
disp('方式3:整流侧定功率,逆变侧定电压')
disp('方式4:整流侧定功率,逆变侧定熄弧角')
disp('方式5:整流侧定触发角,逆变侧定电流')
Controlmode=input('方式:');
%% 交直流计算主循环
for mm=1:1000
H=zeros(p+Ndc);
N=zeros(p+Ndc,q+Ndc);
M=zeros(q+Ndc,p+Ndc);
L=zeros(q+Ndc);
%求ΔPa,ΔQa,ΔPt,ΔQt
Pu=0;Qu=0;
for m=1:p
for k=1:n
Pu=Pu+U(Pn(m))*U(k)*(G(Pn(m),k)*cos(th(Pn(m))-th(k))+B(Pn(m),k)*sin(th(Pn(m))-th(k)));
end
DPa(m)=Pg(Pn(m))-Pl(Pn(m))-Pu;
Pu=0;
end
for m=1:q
for k=1:n
Qu=Qu+U(Qn(m))*U(k)*(G(Qn(m),k)*sin(th(Qn(m))-th(k))-B(Qn(m),k)*cos(th(Qn(m))-th(k)));
end
DQa(m)=Qg(Qn(m))-Ql(Qn(m))-Qu;
Qu=0;
end
for m=1:Ndc
for k=1:n
Pu=Pu+U(DCn(m))*U(k)*(G(DCn(m),k)*cos(th(DCn(m))-th(k))+B(DCn(m),k)*sin(th(DCn(m))-th(k)));
Qu=Qu+U(DCn(m))*U(k)*(G(DCn(m),k)*sin(th(DCn(m))-th(k))-B(DCn(m),k)*cos(th(DCn(m))-th(k)));
end
if any(DCn(m)==Hvdc.con(:,1))
DPt(m)=Pg(DCn(m))-Pl(DCn(m))-Pu-Pd(m);
DQt(m)=Qg(DCn(m))-Ql(DCn(m))-Qu-Qd(m);
else
DPt(m)=Pg(DCn(m))-Pl(DCn(m))-Pu+Pd(m);
DQt(m)=Qg(DCn(m))-Ql(DCn(m))-Qu-Qd(m);%%再仔细想想直流无功的正负号
end
Pu=0;
Qu=0;
end
%矩阵H的形成
for x=1:(p+Ndc)
for y=1:(p+Ndc)
if pn(x)==pn(y)
for m=1:n
H(x,x)=H(x,x)+U(pn(x))*U(m)*(G(pn(x),m)*sin(th(pn(x))-th(m))-B(pn(x),m)*cos(th(pn(x))-th(m)));
end
H(x,x)=H(x,x)-U(pn(x))*U(pn(x))*(G(pn(x),pn(x))*sin(th(pn(x))-th(pn(x)))-B(pn(x),pn(x))*cos(th(pn(x))-th(pn(x))));
else
H(x,y)=-U(pn(x))*U(pn(y))*(G(pn(x),pn(y))*sin(th(pn(x))-th(pn(y)))-B(pn(x),pn(y))*cos(th(pn(x))-th(pn(y))));
end
end
end
Haa=H(Pn-1,Pn-1);
Hat=H(Pn-1,DCn-1);
Hta=H(DCn-1,Pn-1);
Htt=H(DCn-1,DCn-1);
H=[Haa,Hat;Hta,Htt];
%矩阵N的形成
for x=1:(p+Ndc)
for y=1:(q+Ndc)
if pn(x)==qn(y)
for m=1:1:n
N(x,y)=N(x,y)-U(pn(x))*U(m)*(G(pn(x),m)*cos(th(pn(x))-th(m))+B(pn(x),m)*sin(th(pn(x))-th(m)));
end
N(x,y)=N(x,y)+U(pn(x))*U(pn(x))*(G(pn(x),pn(x))*cos(th(pn(x))-th(pn(x)))+B(pn(x),pn(x))*sin(th(pn(x))-th(pn(x))))-2*U(pn(x))^2*G(pn(x),pn(x));
else
N(x,y)=-U(pn(x))*U(qn(y))*(G(pn(x),qn(y))*cos(th(pn(x))-th(qn(y)))+B(pn(x),qn(y))*sin(th(pn(x))-th(qn(y))));
end
end
end
% N(pn==DCn(1),qn==DCn(1))=N(pn==DCn(1),qn==DCn(1))-3*sqrt(2)/pi*cos(Control_ang(1))*Id;
% N(pn==DCn(2),qn==DCn(2))=N(pn==DCn(2),qn==DCn(2))-3*sqrt(2)/pi*cos(Control_ang(2))*Id;
Naa=N(Pn-1,Qn-Qn(1)+1);
Nat=N(Pn-1,DCn-Qn(1)+1);
Nta=N(DCn-1,Qn-Qn(1)+1);
Ntt=N(DCn-1,DCn-Qn(1)+1);
N=[Naa,Nat;Nta,Ntt];
%矩阵M的形成
for x=1:(q+Ndc)
for y=1:(p+Ndc)
if qn(x)==pn(y)
for m=1:1:n
M(x,y)=M(x,y)-U(qn(x))*U(m)*(G(qn(x),m)*cos(th(qn(x))-th(m))+B(qn(x),m)*sin(th(qn(x))-th(m)));
end
M(x,y)=M(x,y)+U(qn(x))*U(qn(x))*(G(qn(x),qn(x))*cos(th(qn(x))-th(qn(x)))+B(qn(x),qn(x))*sin(th(qn(x))-th(qn(x))));
else
M(x,y)=U(qn(x))*U(pn(y))*(G(qn(x),pn(y))*cos(th(qn(x))-th(pn(y)))+B(qn(x),pn(y))*sin(th(qn(x))-th(pn(y))));
end
end
end
Maa=M(Qn-Qn(1)+1,Pn-1);
Mat=M(Qn-Qn(1)+1,DCn-1);
Mta=M(DCn-Qn(1)+1,Pn-1);
Mtt=M(DCn-Qn(1)+1,DCn-1);
M=[Maa,Mat;Mta,Mtt];
%矩阵L的形成
for x=1:(q+Ndc)
for y=1:(q+Ndc)
if qn(x)==qn(y)
for m=1:1:n
L(x,y)=L(x,y)-U(qn(x))*U(m)*(G(qn(x),m)*sin(th(qn(x))-th(m))-B(qn(x),m)*cos(th(qn(x))-th(m)));
end
L(x,y)=L(x,y)+U(qn(x))*U(qn(x))*(G(qn(x),qn(x))*sin(th(qn(x))-th(qn(x)))-B(qn(x),qn(x))*cos(th(qn(x))-th(qn(x))))+2*U(qn(x))^2*B(qn(x),qn(x));
else
L(x,y)=-U(qn(x))*U(qn(y))*(G(qn(x),qn(y))*sin(th(qn(x))-th(qn(y)))-B(qn(x),qn(y))*cos(th(qn(x))-th(qn(y))));
end
end
end
% L(qn==DCn(1),qn==DCn(1))=N(qn==DCn(1),qn==DCn(1))-3*sqrt(2)/pi*cos(Control_ang(1))*Id*tan(fai(1));
% L(qn==DCn(2),qn==DCn(2))=N(qn==DCn(2),qn==DCn(2))-3*sqrt(2)/pi*cos(Control_ang(2))*Id*tan(fai(2));
Laa=L(Qn-Qn(1)+1,Qn-Qn(1)+1);
Lat=L(Qn-Qn(1)+1,DCn-Qn(1)+1);
Lta=L(DCn-Qn(1)+1,Qn-Qn(1)+1);
Ltt=L(DCn-Qn(1)+1,DCn-Qn(1)+1);
L=[Laa,Lat;Lta,Ltt];
%求Δd1----Δd3
for m=1:Ndc
Dd1(m)=Vd(m)-3*sqrt(2)/pi*U(DCn(m))*W(m)+3/pi*Xc(m)*Id;
Dd2(m)=Pd(m)-Vd(m)*Id;
Dd3(m)=Sd(m)-3*sqrt(2)/pi*U(DCn(m))*Id;
Dd4(m)=Sd(m).^2-Pd(m).^2-Qd(m).^2;
end
Dd5=(1/Rdc*Vd(1)-1/Rdc*Vd(2))-Id;
%% JPX JQX JRV JRX
switch Controlmode
case 1
JRX_1=eye(2);
JRX_2=[-3*sqrt(2)/pi*Kt(1)*U(DCn(1)),0;0,-3*sqrt(2)/pi*Kt(2)*U(DCn(2))];
JRX_3=zeros(2);
JRX=[[1;0],JRX_2,zeros(2,6);[-Id;0],JRX_3,JRX_1,JRX_3,JRX_3;[0;0],JRX_3,JRX_3,JRX_1,JRX_3;...
[0;0],JRX_3,[-2*Pd(1),0;0,-2*Pd(2)],[2*Sd(1),0;0,2*Sd(2)],[-2*Qd(1),0;0,-2*Qd(2)];1/Rdc,zeros(1,7),0];
%%为使雅可比矩阵不奇异,将JRX对角线元素为0设为1
JPX=zeros(2,9);
JPX(1,4)=-1;
JPX(2,5)=1;
JQX=zeros(2,9);
JQX(1,8)=-1;
JQX(2,9)=-1;
JRV_1=[-3*sqrt(2)/pi*W(1)*U(DCn(1)),0;0,-3*sqrt(2)/pi*W(2)*U(DCn(2))];
JRV_2=[-3*sqrt(2)/pi*Id*U(DCn(1)),0;0,-3*sqrt(2)/pi*Id*U(DCn(2))];
JRV=[JRV_1;zeros(2);JRV_2;zeros(3,2)];
J=[H,N,[zeros(6,9);JPX];M,L,[zeros(4,9);JQX];zeros(9,8),zeros(9,4),JRV,JRX];
DD=-inv(J)*[DPa;DPt;DQa;DQt;Dd1;Dd2;Dd3;Dd4;Dd5];
%将增量加到U th上
dth(Pn)=DD(1:6);
dth(DCn)=DD(7:8);
dU(Qn)=DD(9:12).*U(Qn);
dU(DCn)=DD(13:14).*U(DCn);
dVd=DD(15);
dW=DD(16:17);
dPd=DD(18:19);
dSd=DD(20:21);
dQd=DD(22:23);
th=th+dth;
U=U+dU;
Vd(1)=Vd(1)+dVd;
W=W+dW;
Pd=Pd+dPd;
Sd=Sd+dSd;
Qd=Qd+dQd;
case 2
JRX_1=eye(2);
JRX_2=[-3*sqrt(2)/pi*Kt(1)*U(DCn(1));0];
JRX_3=zeros(2);
JRX=[JRX_1,JRX_2,zeros(2,6);[-Id,0;0,-Id],[0;0],JRX_1,JRX_3,JRX_3;[0;0],JRX_3,JRX_3,JRX_1,JRX_3;...
[0;0],JRX_3,[-2*Pd(1),0;0,-2*Pd(2)],[2*Sd(1),0;0,2*Sd(2)],[-2*Qd(1),0;0,-2*Qd(2)];1/Rdc,-1/Rdc,zeros(1,7)];
%%为使雅可比矩阵不奇异,将JRX对角线元素为0设为1
JPX=zeros(2,9);
JPX(1,4)=-1;
JPX(2,5)=1;
JQX=zeros(2,9);
JQX(1,8)=-1;
JQX(2,9)=-1;
JRV_1=[-3*sqrt(2)/pi*W(1)*U(DCn(1)),0;0,-3*sqrt(2)/pi*W(2)*U(DCn(2))];
JRV_2=[-3*sqrt(2)/pi*Id*U(DCn(1)),0;0,-3*sqrt(2)/pi*Id*U(DCn(2))];
JRV=[JRV_1;zeros(2);JRV_2;zeros(3,2)];
J=[H,N,[zeros(6,9);JPX];M,L,[zeros(4,9);JQX];zeros(9,8),zeros(9,4),JRV,JRX];
DD=-inv(J)*[DPa;DPt;DQa;DQt;Dd1;Dd2;Dd3;Dd4;Dd5];
%将增量加到U th上
dth(Pn)=DD(1:6);
dth(DCn)=DD(7:8);
dU(Qn)=DD(9:12).*U(Qn);
dU(DCn)=DD(13:14).*U(DCn);
dVd=DD(15:16);
dW=DD(17);
dPd=DD(18:19);
dSd=DD(20:21);
dQd=DD(22:23);
th=th+dth;
U=U+dU;
Vd=Vd+dVd;
W(1)=W(1)+dW;
Pd=Pd+dPd;
Sd=Sd+dSd;
Qd=Qd+dQd;
case 3
JRX_1=eye(2);
JRX_2=[-3*sqrt(2)/pi*Kt(1)*U(DCn(1)),0;0,-3*sqrt(2)/pi*Kt(2)*U(DCn(2))];
JRX_3=zeros(2);
JRX=[[1;0],JRX_2,zeros(2,1),JRX_3,JRX_3,[3/pi*Xc(1);3/pi*Xc(2)];[-Id;0],JRX_3,[0;1],JRX_3,JRX_3,[-Vd(1);-Vd(2)];[0;0],JRX_3,[0;0],JRX_1,JRX_3,[-3*sqrt(2)/pi*Kt(1)*U(DCn(1));-3*sqrt(2)/pi*Kt(2)*U(DCn(2))];...
[0;0],JRX_3,[0;-2*Pd(2)],[2*Sd(1),0;0,2*Sd(2)],[-2*Qd(1),0;0,-2*Qd(2)],[0;0];1/Rdc,zeros(1,7),-1];
%%为使雅可比矩阵不奇异,将JRX对角线元素为0设为1
JPX=zeros(2,9);
JPX(2,4)=1;
JQX=zeros(2,9);
JQX(1,7)=-1;
JQX(2,8)=-1;
JRV_1=[-3*sqrt(2)/pi*W(1)*U(DCn(1)),0;0,-3*sqrt(2)/pi*W(2)*U(DCn(2))];
JRV_2=[-3*sqrt(2)/pi*Id*U(DCn(1)),0;0,-3*sqrt(2)/pi*Id*U(DCn(2))];
JRV=[JRV_1;zeros(2);JRV_2;zeros(3,2)];
%% 雅可比矩阵
J=[H,N,[zeros(6,9);JPX];M,L,[zeros(4,9);JQX];zeros(9,8),zeros(9,4),JRV,JRX];
DD=-inv(J)*[DPa;DPt;DQa;DQt;Dd1;Dd2;Dd3;Dd4;Dd5];
%将增量加到U th上
dth(Pn)=DD(1:6);
dth(DCn)=DD(7:8);
dU(Qn)=DD(9:12).*U(Qn);
dU(DCn)=DD(13:14).*U(DCn);
dVd=DD(15);
dW=DD(16:17);
dPd=DD(18);
dSd=DD(19:20);
dQd=DD(21:22);
dId=DD(23);
th=th+dth;
U=U+dU;
Vd(1)=Vd(1)+dVd;
W=W+dW;
Pd(2)=Pd(2)+dPd;
Sd=Sd+dSd;
Qd=Qd+dQd;
Id=Id+dId;
case 4
JRX_1=eye(2);
JRX_2=[-3*sqrt(2)/pi*Kt(1)*U(DCn(1));0];
JRX_3=zeros(2);
JRX=[JRX_1,JRX_2,zeros(2,1),JRX_3,JRX_3,[3/pi*Xc(1);3/pi*Xc(2)];[-Id,0;0,-Id],[0;0],[0;1],JRX_3,JRX_3,[-Vd(1);-Vd(2)];[0;0],JRX_3,[0;0],JRX_1,JRX_3,[-3*sqrt(2)/pi*Kt(1)*U(DCn(1));-3*sqrt(2)/pi*Kt(2)*U(DCn(2))];...
[0;0],JRX_3,[0;-2*Pd(2)],[2*Sd(1),0;0,2*Sd(2)],[-2*Qd(1),0;0,-2*Qd(2)],[0;0];1/Rdc,-1/Rdc,zeros(1,6),-1];
%%为使雅可比矩阵不奇异,将JRX对角线元素为0设为1
JPX=zeros(2,9);
JPX(2,4)=1;
JQX=zeros(2,9);
JQX(1,7)=-1;
JQX(2,8)=-1;
JRV_1=[-3*sqrt(2)/pi*W(1)*U(DCn(1)),0;0,-3*sqrt(2)/pi*W(2)*U(DCn(2))];
JRV_2=[-3*sqrt(2)/pi*Id*U(DCn(1)),0;0,-3*sqrt(2)/pi*Id*U(DCn(2))];
JRV=[JRV_1;zeros(2);JRV_2;zeros(3,2)];
%% 雅可比矩阵
J=[H,N,[zeros(6,9);JPX];M,L,[zeros(4,9);JQX];zeros(9,8),zeros(9,4),JRV,JRX];
DD=-inv(J)*[DPa;DPt;DQa;DQt;Dd1;Dd2;Dd3;Dd4;Dd5];
%将增量加到U th上
dth(Pn)=DD(1:6);
dth(DCn)=DD(7:8);
dU(Qn)=DD(9:12).*U(Qn);
dU(DCn)=DD(13:14).*U(DCn);
dVd=DD(15:16);
dW=DD(17);
dPd=DD(18);
dSd=DD(19:20);
dQd=DD(21:22);
dId=DD(23);
th=th+dth;
U=U+dU;
Vd=Vd+dVd;
W(1)=W(1)+dW;
Pd(2)=Pd(2)+dPd;
Sd=Sd+dSd;
Qd=Qd+dQd;
Id=Id+dId;
case 5
JRX_1=eye(2);
JRX_2=[0;-3*sqrt(2)/pi*Kt(2)*U(DCn(2))];
JRX_3=zeros(2);
JRX=[JRX_1,JRX_2,zeros(2,1),JRX_3,JRX_3,[3/pi*Xc(1);3/pi*Xc(2)];[-Id,0;0,-Id],[0;0],[1,0;0,1],JRX_3,JRX_3;[0;0],JRX_3,JRX_3,JRX_1,JRX_3;...
[0;0],JRX_3,[-2*Pd(1),0;0,-2*Pd(2)],[2*Sd(1),0;0,2*Sd(2)],[-2*Qd(1),0;0,-2*Qd(2)];1/Rdc,-1/Rdc,zeros(1,6),0];
%%为使雅可比矩阵不奇异,将JRX对角线元素为0设为1
JPX=zeros(2,9);
JPX(2,4)=1;
JQX=zeros(2,9);
JQX(1,7)=-1;
JQX(2,8)=-1;
JRV_1=[-3*sqrt(2)/pi*W(1)*U(DCn(1)),0;0,-3*sqrt(2)/pi*W(2)*U(DCn(2))];
JRV_2=[-3*sqrt(2)/pi*Id*U(DCn(1)),0;0,-3*sqrt(2)/pi*Id*U(DCn(2))];
JRV=[JRV_1;zeros(2);JRV_2;zeros(3,2)];
%% 雅可比矩阵
J=[H,N,[zeros(6,9);JPX];M,L,[zeros(4,9);JQX];zeros(9,8),zeros(9,4),JRV,JRX];
DD=-inv(J)*[DPa;DPt;DQa;DQt;Dd1;Dd2;Dd3;Dd4;Dd5];
%将增量加到U th上
dth(Pn)=DD(1:6);
dth(DCn)=DD(7:8);
dU(Qn)=DD(9:12).*U(Qn);
dU(DCn)=DD(13:14).*U(DCn);
dVd=DD(15:16);
dW=DD(17);
dPd=DD(18:19);
dSd=DD(20:21);
dQd=DD(22:23);
th=th+dth;
U=U+dU;
Vd=Vd+dVd;
W(2)=W(2)+dW;
Pd=Pd+dPd;
Sd=Sd+dSd;
Qd=Qd+dQd;
end
AP=abs(DD);%取模值
%判断是否收敛
if(max(AP)<1e-5) %E是之前定义的零阵
break;
end
kk=kk+1;
end
if mm==200
disp('注意:结果不收敛!');
end
disp(' 迭代次数:')
kk
disp('电压幅值:')
U
toc
。。。。。。。略
边栏推荐
- 04-SDRAM: Read Operation (Burst)
- 安装和使用uView
- 一文读懂 MongoDB 和 MySQL 的差异
- 运行 npm 会弹出询问 “你要如何打开这个文件?“
- Foreign trade website optimization - foreign trade website optimization tutorial - foreign trade website optimization software
- DDL+DML+DQL
- 深度解析 z-index
- 数据库概论 - MySQL的简单介绍
- 【Star项目】小帽飞机大战(八)
- 【编程题】【Scratch三级】2022.03 冬天下雪了
猜你喜欢
【微服务】Nacos集群搭建以及加载文件配置
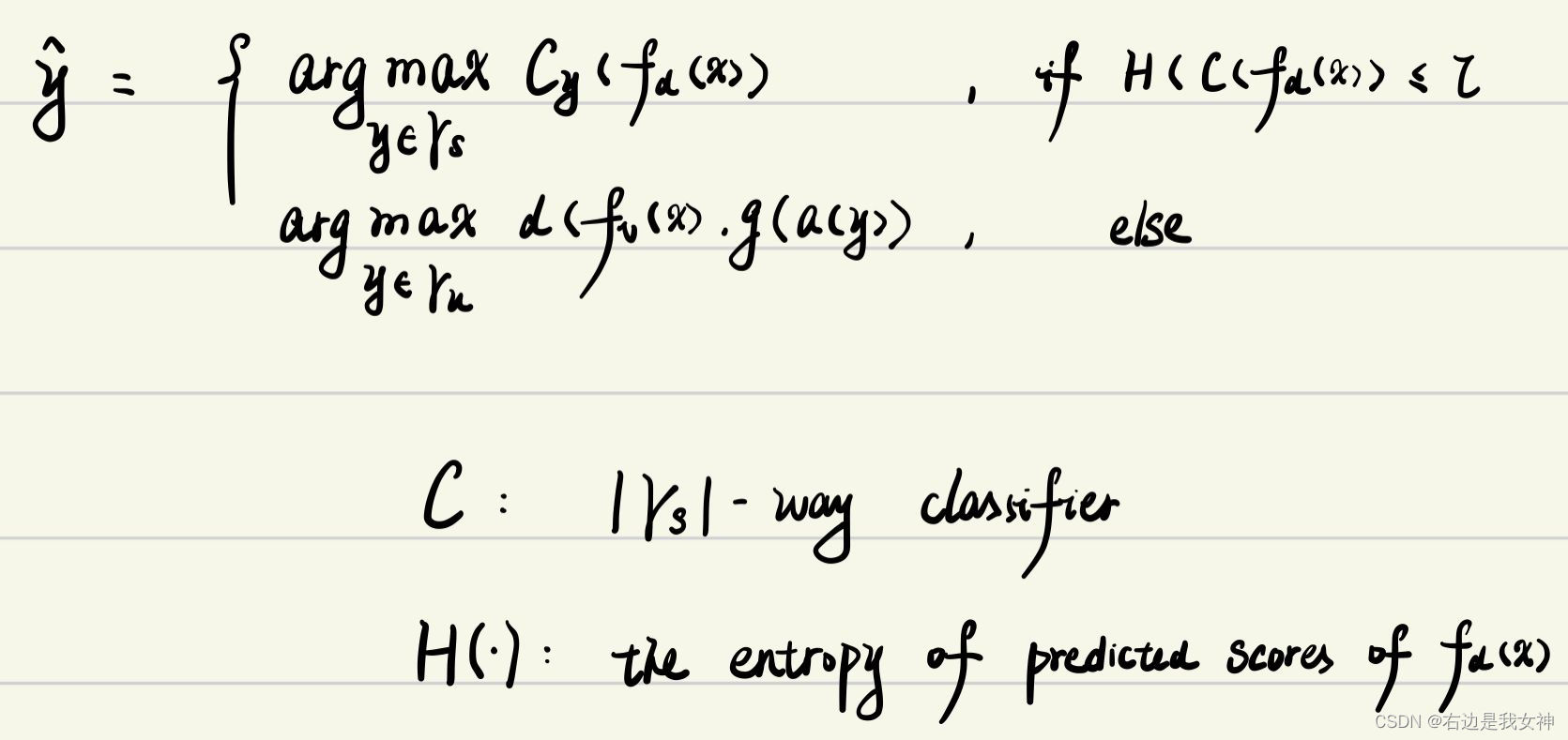
零样本学习&Domain-aware Visual Bias Eliminating for Generalized Zero-Shot Learning
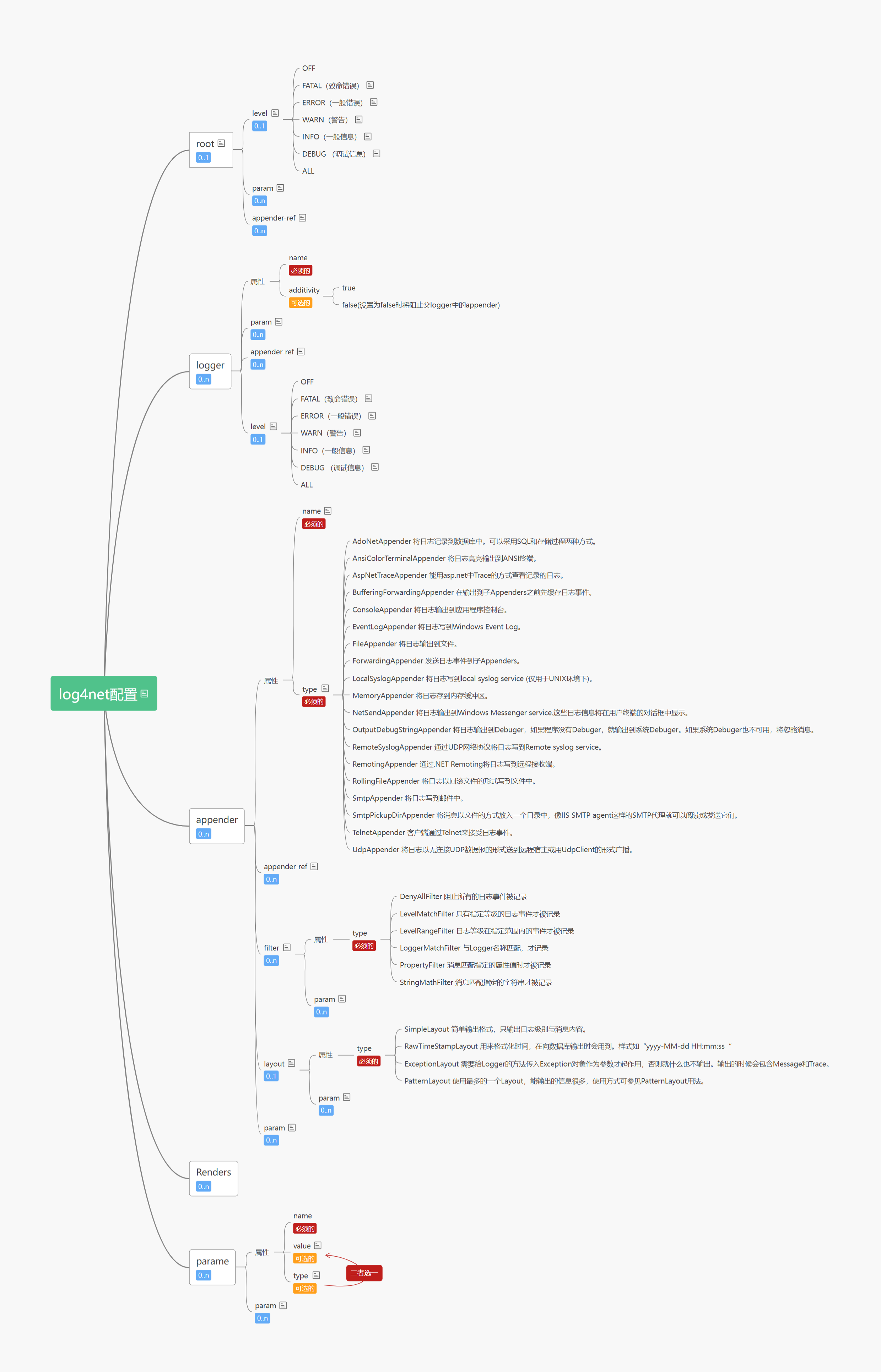
Log4net 思维导图
【网络攻防】常见的网络攻防技术——黑客攻防(通俗易懂版)

讲解实例+详细介绍@Resource与@Autowired注解的区别(全网最全)
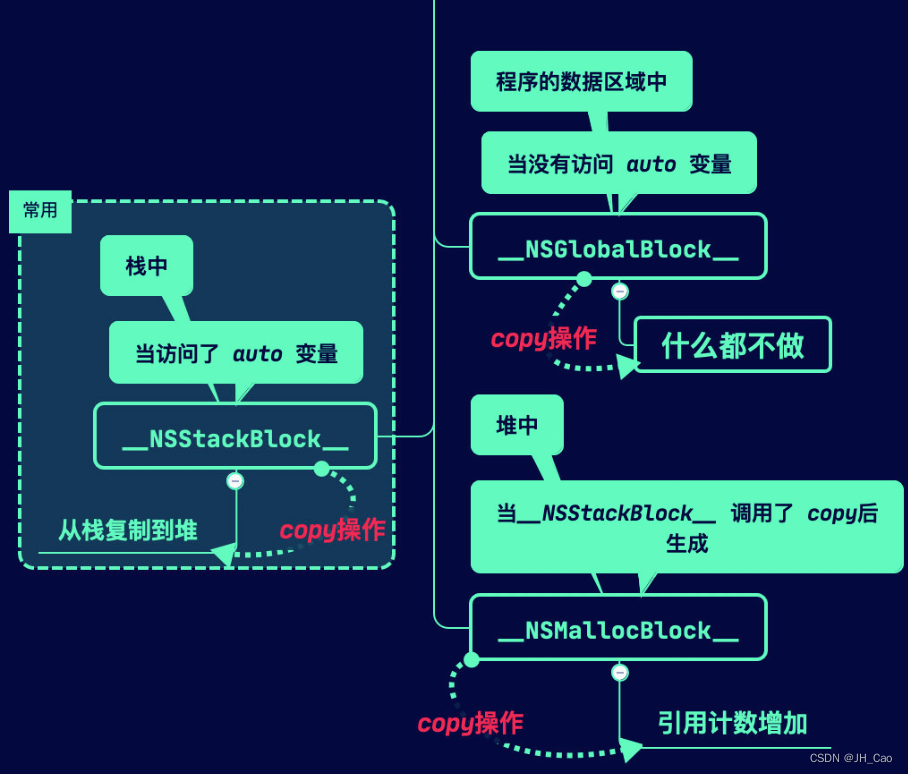
iOS大厂面试查漏补缺
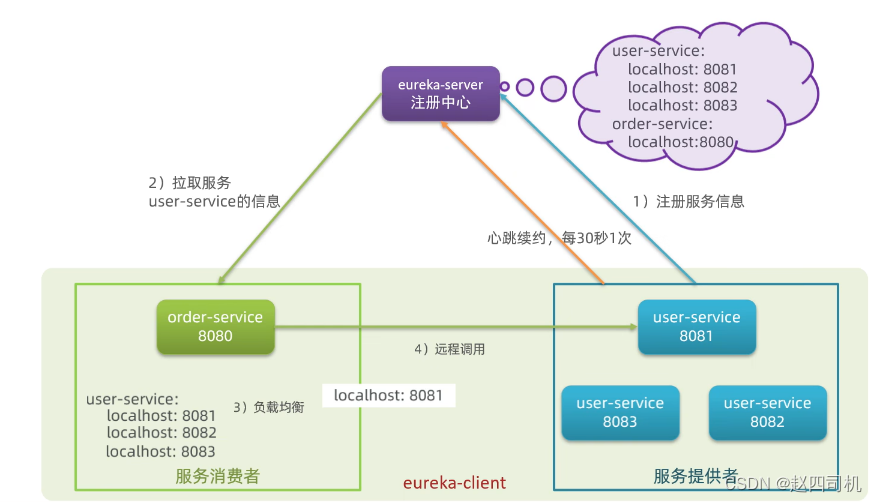
【微服务】 微服务学习笔记二:Eureka注册中心的介绍及搭建
外贸网站优化-外贸网站优化教程-外贸网站优化软件
LeetCode:952. 按公因数计算最大组件大小【欧拉筛 + 并查集】

How to use repeating-linear-gradient
随机推荐
Difficulty comparison between high concurrency and multithreading (easy to confuse)
Log4net 思维导图
【Go语言入门教程】Go语言简介
How to use repeating-linear-gradient
Automatic translation software - batch batch automatic translation software recommendation
线程唤醒机制
Chapter 17: go back to find the entrance to the specified traverse, "ma bu" or horse stance just look greedy, no back to search traversal, "ma bu" or horse stance just look recursive search NXM board
批量翻译软件免费【2022最新版】
【微服务】Nacos集群搭建以及加载文件配置
In-depth analysis of z-index
【云原生】3.3 Kubernetes 中间件部署实战
Project exercise - memorandum (add, delete, modify, check)
Jobject 使用
Install the gstreamer development dependency library to the project sysroot directory
MySql的安装配置超详细教程与简单的建库建表方法
知识、创新、回报。
One of the small practical projects - food alliance ordering system
Moment.js常用方法
MySQL笔记下
简单谈谈Feign