Easy to understand Laplace smoothing of naive Bayesian classification

Click on the above “ Xiaobai studies vision ”, Optional plus " Star standard " or “ Roof placement ”

 Heavy dry goods , First time delivery 

The four characteristics of this boy are that he is not handsome , Bad character , Short height , No progress , We finally came to the conclusion that girls don't marry ！ Many people say that this is a question of giving away points , Ha ha ha ha . We also use mathematical algorithms to show that you can't get a wife if you don't rely on the spectrum ！

So let's take another example , Suppose another couple , Of the couple , The four characteristics of boys are , Handsome , Good personality , Tall , progresses , So is his girlfriend married or not ？ There may be a little friend who says that this is a question of giving points , Is it right? , Let's speak with facts ！

Let's introduce the Laplace smoothing process through an example ！

Start with an example

Or the following training data ：

The four feature sets look like { handsome , Not handsome }、 character { Burst , good , Not good. }、 height { high , in , Short }、 Make progress or not { progresses , No progress }

At this time, we asked the boy to be handsome in four characteristics , Good personality , Tall , In the case of progress , His corresponding probability of marrying or not marrying is larger or smaller , And then come to the conclusion ！

That is to compare p( marry | Handsome , Good personality , Tall , progresses ) And p( Never marry | Handsome , Good personality , Tall , progresses ) The probability of .

According to the naive Bayesian algorithm formula , We can get the following formula ：

Because the denominator of both is p( Handsome )、p( Good personality )、p( Tall )、p（ progresses ）, Then we don't count the denominator , When comparing, only compare the molecular sizes of the two formulas .

well , Now let's start to calculate , First, under the condition of four characteristics , The probability of marriage .

We need to calculate separately p（ Good personality | marry ）、p( Handsome | marry )、p( Tall | marry )、p( progresses | marry )

First, let's calculate p( Good personality | marry )=？ We look at the training data , Found as follows ：

There is no data with this feature , that p（ Good personality | marry ） = 0, Then we can see the problem , According to the formula ：

Our last p( marry | Handsome 、 Good personality 、 Tall 、 progresses ) Because of a p（ Good personality | marry ） by 0, And the whole probability is 0, This is obviously wrong .

This error is caused by insufficient training , Will greatly reduce the quality of the classifier . To solve this problem , We introduce Laplace calibration （ This leads to our Laplace smoothing ）, Its idea is very simple , Is to add the count of all divisions under each category 1, In this way, if the number of training sample sets is large enough , No impact on results , And the above frequency is solved 0 An awkward situation .

The formula for introducing Laplace smoothing is as follows ：

among ajl, On behalf of the j Characteristics l A choice ,Sj On behalf of the j Number of features ,K Represents the number of species .

λ by 1, It's easy to understand , After adding Laplace smoothing , The probability of occurrence is 0 The situation of , It also ensures that each value is 0 To 1 Within the scope of , It also ensures that the final peace is 1 Probabilistic properties of ！

We can understand this formula more deeply through the following examples ：（ Now we are adding Laplacian smoothing ）

Add Laplacian smoothing

We need to calculate separately first p（ Good personality | marry ）、p( Handsome | marry )、p( Tall | marry )、p( progresses | marry ),p( marry )

p( Good personality | marry )=？ The statistics that meet the requirements are shown in the red part below

No satisfaction is the condition for a good personality , But the probability is not 0, According to the formula after Laplace smoothing , The number of personality traits is good , good , Not good. , Three situations , that S_j by 3, Then the final probability is 1/9 （ The number of people married is 6+ The number of features is 3）

p( Handsome | marry )=？ Statistics of the items that meet the conditions are shown in the red part below ：

It can be seen from the above figure that what meets the requirements is 3 individual , According to the formula after Laplace smoothing , The number of facial features is handsome , Not handsome , Two cases , that S_j by 2, Then the final probability p( Handsome | marry ) by 4/8 （ The number of people married is 6+ The number of features is 2）

p（ Tall | marry ） = ？ Statistics of the items that meet the conditions are shown in the red part below ：

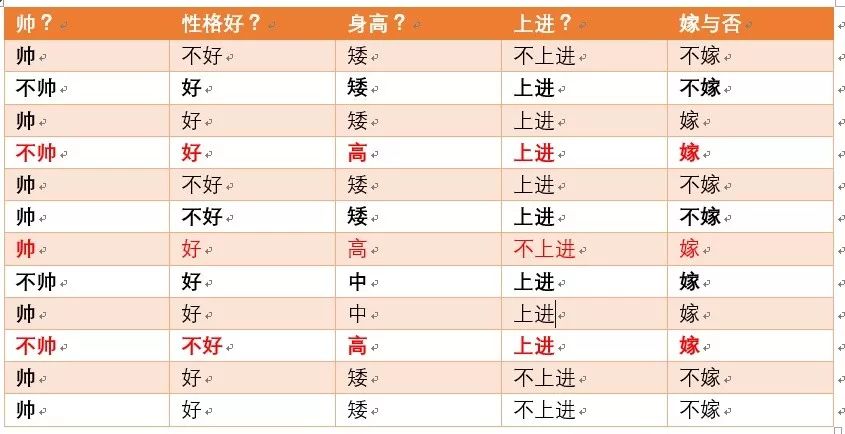
It can be seen from the above figure that what meets the requirements is 3 individual , According to the formula after Laplace smoothing , The number of height characteristics is high , in , Short condition , that S_j by 3, Then the final probability p( Tall | marry ) by 4/9 （ The number of people married is 6+ The number of features is 3）

p（ progresses | marry )=？ The statistics that meet the requirements are shown in the red part below ：

It can be seen from the above figure that what meets the requirements is 5 individual , According to the formula after Laplace smoothing , The number of progressive features is progressive , Poor performance , that S_j by 2, Then the final probability p( progresses | marry ) by 6/8 （ The number of people married is 6+ The number of features is 2）

p( marry ) = ？ The following red markings meeting the requirements ：

It can be seen from the above figure that what meets the requirements is 6 individual , According to the formula after Laplace smoothing , The number of species is , Not married , that K by 2, Then the final probability p( marry ) by 7/14 = 1/2 （ The number of people married is 6+ The number of species is 2）

So far , We have calculated that under the condition of the boy , The probability of marriage is ：

p( marry | Handsome 、 Good personality 、 Tall 、 progresses ) = 1/9*4/8*4/9*6/8*1/2

Now we need to calculate p( Never marry | Handsome 、 Good personality 、 Tall 、 progresses ) Probability , Then compare with the above values , The algorithm is exactly the same as above ！ Here, too .

We need to estimate p( Handsome | Never marry )、p( Good personality | Never marry )、p( Tall | Never marry )、p（ progresses | Never marry ）,p（ Never marry ） What are the probabilities of .

p（ Handsome | Never marry ）=？ Meet the requirements as indicated in red below ：

It can be seen from the above figure that what meets the requirements is 5 individual , According to the formula after Laplace smoothing , The number of handsome features is not handsome , Handsome situation , that S_j by 2, Then the final probability p( Not handsome | Never marry ) by 6/8 （ The number of unmarried people is 6+ The number of features is 2）

p（ Good personality | Never marry ）=？ Meet the requirements as indicated in red below ：

No satisfaction is the condition for a good personality , But the probability is not 0, According to the formula after Laplace smoothing , The number of personality traits is good , good , Not good. , Three situations , that S_j by 3, Then the final probability p（ Good personality | Never marry ） by 1/9 （ The number of unmarried people is 6+ The number of features is 3）

p（ Tall | Never marry ）=？ Meet the requirements as indicated in red below ：

No one is tall , But the probability is not 0, According to the formula after Laplace smoothing , The number of height characteristics is high , in , Short , Three situations , that S_j by 3, Then the final probability p( Tall | Never marry ) by 1/9 （ The number of unmarried people is 6+ The number of features is 3）

p（ progresses | Never marry ）=？ Meet the requirements as indicated in red below ：

It can be seen from the above figure that what meets the requirements is 3 individual , According to the formula after Laplace smoothing , The number of progressive features is progressive , Poor performance , that S_j by 2, Then the final probability p( progresses | Never marry ) by 4/8 （ The number of unmarried people is 6+ The number of features is 2）

p（ Never marry ）=？ If it meets the requirements, such as red marking ：

It can be seen from the above figure that what meets the requirements is 6 individual , According to the formula after Laplace smoothing , The number of species is , Not married , that K by 2, Then the final probability p( Never marry ) by 7/14 = 1/2 （ The number of unmarried people is 6+ The number of species is 2）

So far , We have calculated that under the condition of the boy , The probability of not marrying is ：

p( Never marry | Handsome 、 Good personality 、 Tall 、 progresses ) = 5/8*1/9*1/9*3/8*1/2

Conclusion

So we can get

p( marry | Handsome 、 Good personality 、 Tall 、 progresses ) = 1/9*4/8*4/9*6/8*1/2 > p( Never marry | Handsome 、 Good personality 、 Tall 、 progresses ) = 6/8*1/9*1/9*4/8*1/2

So we can boldly tell girls , Such a good man , Bayes told you , To marry ！！！

This is the whole algorithm process after we use Laplace smoothing ！

I hope it will be helpful to your understanding ~ Welcome to communicate with me ！

The good news ！

Xiaobai learns visual knowledge about the planet

Open to the outside world

 download 1：OpenCV-Contrib Chinese version of extension module 

 stay 「 Xiaobai studies vision 」 Official account back office reply ： Extension module Chinese course , You can download the first copy of the whole network OpenCV Extension module tutorial Chinese version , Cover expansion module installation 、SFM Algorithm 、 Stereo vision 、 Target tracking 、 Biological vision 、 Super resolution processing and other more than 20 chapters .


 download 2：Python Visual combat project 52 speak 
 stay 「 Xiaobai studies vision 」 Official account back office reply ：Python Visual combat project , You can download, including image segmentation 、 Mask detection 、 Lane line detection 、 Vehicle count 、 Add Eyeliner 、 License plate recognition 、 Character recognition 、 Emotional tests 、 Text content extraction 、 Face recognition, etc 31 A visual combat project , Help fast school computer vision .


 download 3：OpenCV Actual project 20 speak 
 stay 「 Xiaobai studies vision 」 Official account back office reply ：OpenCV Actual project 20 speak , You can download the 20 Based on OpenCV Realization 20 A real project , Realization OpenCV Learn advanced .


 Communication group 

 Welcome to join the official account reader group to communicate with your colleagues , There are SLAM、 3 d visual 、 sensor 、 Autopilot 、 Computational photography 、 testing 、 Division 、 distinguish 、 Medical imaging 、GAN、 Wechat groups such as algorithm competition （ It will be subdivided gradually in the future ）, Please scan the following micro signal clustering , remarks ：” nickname + School / company + Research direction “, for example ：” Zhang San  +  Shanghai Jiaotong University  +  Vision SLAM“. Please note... According to the format , Otherwise, it will not pass . After successful addition, they will be invited to relevant wechat groups according to the research direction . Please do not send ads in the group , Or you'll be invited out , Thanks for your understanding ~