Count the logarithm of points that cannot reach each other in an undirected graph [classic adjacency table building +dfs Statistics - > query set optimization] [query set manual / write details]

Preface

Given nodes and edges ( Node pair ), Find the connected components and their variants . The first idea is based on nodes and node pairs ( edge ) To establish adjacency matrix , stay DFS To do things .
But there is also an idea closely related to connected components , Union checking set , It does not create a complete graph , But can do the corresponding thing , So the running time is short .
It takes the original graph , Select a node as the root node , All direct / Indirectly connected nodes act as child nodes , Can solve many connected components / Connected component variation problem .
In addition to the above advantages , I feel its array hash Than hashMap fast , After all, the array is JVM level , And continuous inner layer distribution , Than API fast .

One 、 Count the logarithm of points that cannot reach each other in an undirected graph

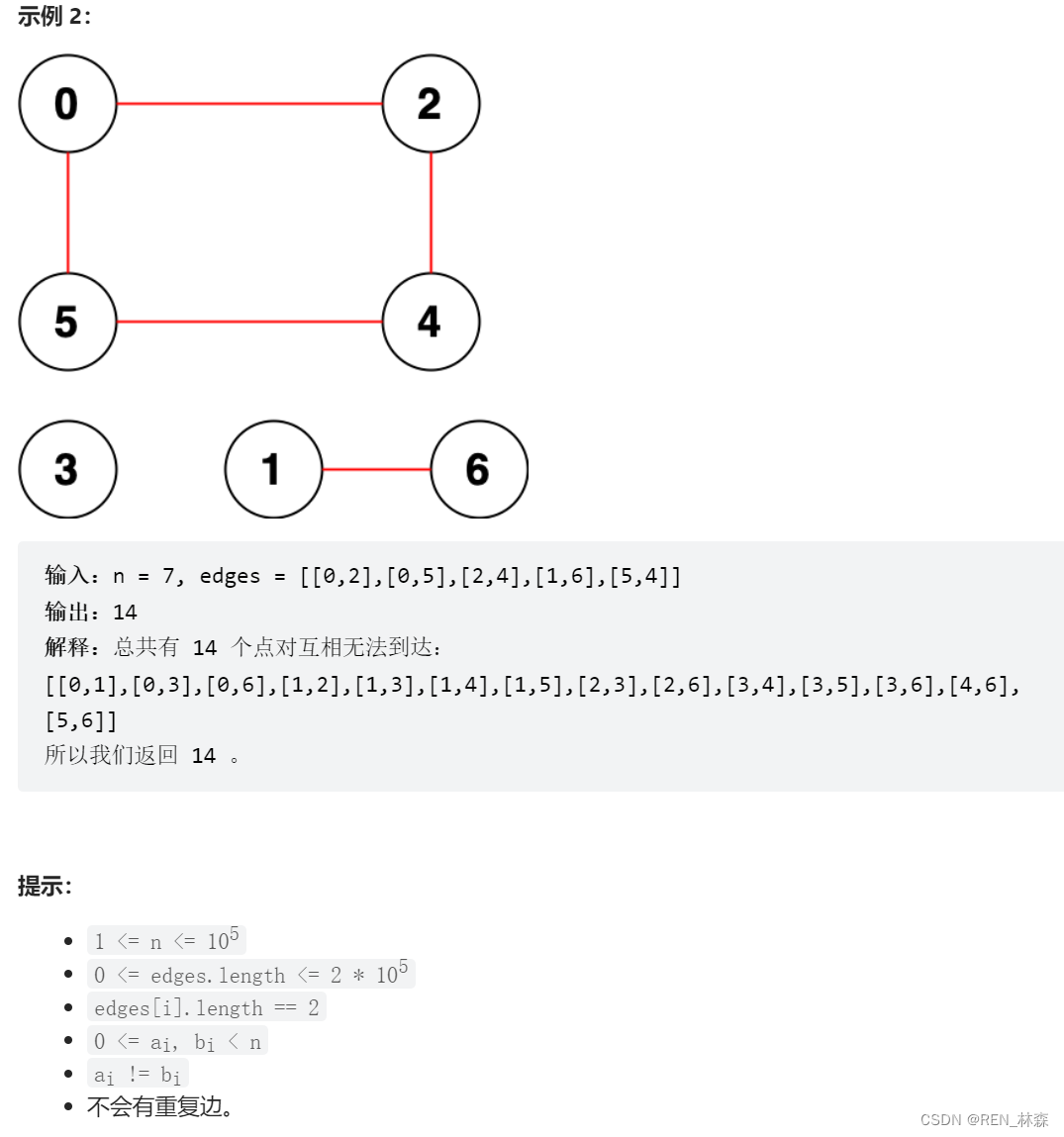
Two 、 Classic adjacency table +DFS Statistics -> And look up set optimization

1、 Classic adjacency table +DFS Statistics

public class CountPairs {
    
    public long countPairs(int n, int[][] edges) {
    
        //  Join all nodes .
        for (int i = 0; i < n; i++) addNode(i);
        for (int[] edge : edges) addEdge(edge[0], edge[1]);
        List<Long> arr = new ArrayList<>();
        for (int i = 0; i < n; i++) if (graph.containsKey(i)) arr.add(dfs(i));
        //
        long[] prefix = new long[arr.size()];
        long sum = 0, ans = 0;
        int idx = 0;

        for (long i : arr) prefix[idx++] = (sum += i);
        for (int i = 0; i < arr.size() - 1; i++) ans += arr.get(i) * (prefix[arr.size() - 1] - prefix[i]);
        return ans;
    }

    private long dfs(int n) {
    
        long rs = 1;
        Set<Integer> next = graph.get(n);
        if (next == null) return rs;
        graph.remove(n);
        for (Integer i : next) {
    
            if (graph.containsKey(i)) rs += dfs(i);
        }
        return rs;
    }

    private void addEdge(int a, int b) {
    
        addNode(a);
        addNode(b);

        graph.get(a).add(b);
        graph.get(b).add(a);
    }

    private void addNode(int b) {
    
        if (!graph.containsKey(b)) graph.put(b, new HashSet<>());
    }

    Map<Integer, Set<Integer>> graph = new HashMap<>();
}

2、 And look up set optimization

//  Practice hashing , It is a sharp weapon about connected components .
class CountPairs2 {
    
    public long countPairs(int n, int[][] edges) {
    
        //  And the first step of the search set standard ： initialization .
        int[] father = new int[n];
        Arrays.fill(father, -1);
        //  And the second step of the search set standard ：union
        cnt = n;//  Here, I want to count the number of connected components , The number of nodes of each connected component will be counted , You can use arrays , Not expandable list.|  Or directly list
        for (int[] edge : edges) union(father, edge[0], edge[1]);
        //  Nonspecific logic , The specific requirements shall be specified .
        //  Count the number of nodes of each connected component .
        int[] arr = new int[cnt];
        cnt = 0;
        for (int f : father) if (f < 0) arr[cnt++] = -f;
        //  Nonspecific logic , The specific requirements shall be specified .
        //  Get the number of nodes with different connected components , Use prefixes and , Space for time .
        long[] prefix = new long[arr.length];
        long sum = 0;
        cnt = 0;
        for (int a : arr) prefix[cnt++] = (sum += a);
        //  Get the results 
        long ans = 0;
        for (int i = 0; i < arr.length - 1; i++) ans += arr[i] * (prefix[prefix.length - 1] - prefix[i]);
        return ans;
    }

    int cnt = 0;//  The number of connected components .

    private void union(int[] father, int m, int n) {
    
        //  And the third step of the search set standard ：findFather
        int r1 = findFather(father, m);
        int r2 = findFather(father, n);
        //  Not the same logic , Write according to the actual situation .
        if (r1 != r2) {
    
            //  Combine the two , Just take one as the root , Get the number of nodes of the whole tree , A negative number here means .
            father[r1] += father[r2];
            //  And take the other as a subtree , And modify its root node .
            father[r2] = r1;
            //  Optional operation , When used list when , Are not .
            --cnt;
        }
    }

    private int findFather(int[] father, int r) {
    
        //  All the way back to the root , And take the root as the root of each node on the path .
        //  Embodied in  if (father[r] != r) father[r] = findFather(father, father[r]); return father[r]; This will tile the deep trees .

        //  But not here , Because the value of the root node is not equal to its subscript , It's a negative number , Count the number of nodes .
        //  There is a need to change the traditional practice , Be flexible .

        //  If the node is the root 
        if (father[r] < 0) return r;
        return father[r] = findFather(father, father[r]);
    }
}

summary

1） Classic adjacency table establishment + stay dfs Traverse （ Figure basis of operation ） Do your own thing .
2） And look up the set to change the shape of the graph , But it does not affect problem solving , Then its reduced running time becomes an advantage .
3） In addition to the above advantages , I feel its array hash Than hashMap fast , After all, the array is JVM level , And continuous inner layer distribution , Than API fast .
4） And the classic three steps of searching sets , Each step can be based on specific needs , And flexible writing . The specific three steps are ： Initialize array father[size]{}( Array hash very nice)、union(int[],int,int) Connect two nodes 、findFather(int[],int) Find the root node .

reference

[1] LeetCode Count the logarithm of points that cannot reach each other in an undirected graph