当前位置:网站首页>Codeforces Global Round 21(A-E)
Codeforces Global Round 21(A-E)
2022-07-04 08:34:00 【ccsu_yuyuzi】
目录
C. Fishingprince Plays With Array
A. NIT orz
签到
#include<map>
#include<cmath>
#include<set>
#include<queue>
#include<string>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_set>
#include<unordered_map>
#define int long long
using namespace std;
const int N =5e5+10,mod=998244353;
void solve()
{
int n,z,ans=0,x;
cin>>n>>z;
for(int i=1;i<=n;i++)
{
cin>>x;
if((x|z)>=ans)
ans=x|z;
}
cout<<ans<<"\n";
return ;
}
signed main()
{
int t;
cin>>t;
while(t--)
solve();
return 0;
}B. NIT Destroys the Universe
题意:给你一个数组,我们可以进行操作:选择一个区间,让这个区间的数字全部变成这个区间没有出现过的最小的非负数(mex).问多少步可以把这个数组全部置为0.
思路:最多只需要两步就可以让全部置为0,我们一开始选择整个数组变成他们的mex,这个时候所有的数字都会变成一个非0的数(如果不包含0一步即可,直接全部变成0).第二步再次选择整个数组,这个时候0肯定不存在,所以就会变成0.
#include<map>
#include<cmath>
#include<set>
#include<queue>
#include<string>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_set>
#include<unordered_map>
#define int long long
using namespace std;
const int N =5e5+10,mod=998244353;
int arr[100005];
void solve()
{
int n,cnt=0;
cin>>n;
for(int i=1;i<=n;i++)
cin>>arr[i];
if(arr[1]!=0)
cnt++;
for(int i=2;i<=n;i++)
if(arr[i]>0&&arr[i-1]==0)
cnt++;
if(cnt==0)
cout<<"0";
else if(cnt==1)
cout<<"1";
else
cout<<"2";
cout<<"\n";
return ;
}
signed main()
{
int t;
cin>>t;
while(t--)
solve();
return 0;
}C. Fishingprince Plays With Array
Problem - C - Codeforces https://codeforces.com/contest/1696/problem/C
https://codeforces.com/contest/1696/problem/C
题意:给你两个长度和两个数组,还有一个限定长度k,当数组中某个元素是k的倍数时,就可以把它分成k个这个元素除以k的平均数.同理,有k个相连的相同的数时,可以合并成一个数字,为k乘以这个相同的数.问可否有第一个数组得到第二个数组.
思路:把两个数组按照第一条规则拆分,看全部拆分后的两个数组是否相同即可,注意数据范围,我是用结构体来记录的数字的值和连续个数.
#include<map>
#include<cmath>
#include<set>
#include<queue>
#include<string>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_set>
#include<unordered_map>
#define int long long
using namespace std;
int a[50004],b[50004];
struct node
{
int num,sum;
}anum[50004],bnum[50004];
void solve()
{
int n,m,k,x,cnt;
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
anum[i]={-1,0};
}
scanf("%lld",&k);
for(int i=1;i<=k;i++)
{
scanf("%lld",&b[i]);
bnum[i]={-1,0};
}
int tot1=1;
for(int i=1;i<=n;i++)
{
x=a[i];
cnt=1;
while(x%m==0)
{
x/=m;
cnt*=m;
}
if(x==anum[tot1].num)
anum[tot1].sum+=cnt;
else
{
if(anum[tot1].num!=-1)
tot1++;
anum[tot1].num=x;
anum[tot1].sum=cnt;
}
}
int tot2=1;
for(int i=1;i<=k;i++)
{
x=b[i];
cnt=1;
while(x%m==0)
{
x/=m;
cnt*=m;
}
if(x==bnum[tot2].num)
bnum[tot2].sum+=cnt;
else
{
if(bnum[tot2].num!=-1)
tot2++;
bnum[tot2].num=x;
bnum[tot2].sum=cnt;
}
}
if(tot1!=tot2)
{
printf("NO\n");
return ;
}
for(int i=1;i<=tot1;i++)
{
if(anum[i].num!=bnum[i].num||anum[i].sum!=bnum[i].sum)
{
printf("NO\n");
return ;
}
}
printf("YES\n");
return ;
}
signed main()
{
int t;
cin>>t;
while(t--)
solve();
return 0;
}D. Permutation Graph
Problem - D - Codeforces https://codeforces.com/contest/1696/problem/D
https://codeforces.com/contest/1696/problem/D
题意:给出一个数组,如果满足 i 和 j 分别是区间内[a[i] a[i+1] ......a[j] ]的最小值和最大值,则之间有边,问从1号点走到n号点至少需要多少步.
思路:看到区间最大最小值肯定直接上st表或者线段树进行查询.我们先对着整个区间进行最大最小值的查询.如果查询到了,就说明两个点可以进行连线,这两个点连接了之后,他们所包围的区间就不用在进行连接处理,因为已经求出了这一段的最短路,就是1,那么再针对没有找到最短路的区间进行上述操作递归递归即可.(因为上述操作要求我们要知道最大最小值的位置,所以还要开一个pos数组记录位置)
#include<map>
#include<cmath>
#include<set>
#include<queue>
#include<string>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_set>
#include<unordered_map>
using namespace std;
struct node
{
int l,r,mx,mn;
}tr[4*250004];
int a[250004],pos[250004];
void build(int node,int l,int r)
{
tr[node].l=l,tr[node].r=r;
if(l==r)
{
tr[node].mx=a[l];
tr[node].mn=a[l];
return ;
}
int mid=(l+r)>>1;
build(node*2,l,mid);
build(node*2+1,mid+1,r);
tr[node].mx=max(tr[node*2].mx,tr[node*2+1].mx);
tr[node].mn=min(tr[node*2].mn,tr[node*2+1].mn);
return;
}
int querymx(int node,int l,int r)
{
if(l<=tr[node].l&&tr[node].r<=r)
return tr[node].mx;
int mid=(tr[node].l+tr[node].r)>>1;
int ans=-1e9;
if(l<=mid)
ans=max(ans,querymx(node*2,l,r));
if(r>mid)
ans=max(ans,querymx(node*2+1,l,r));
return ans;
}
int querymn(int node,int l,int r)
{
if(l<=tr[node].l&&tr[node].r<=r)
return tr[node].mn;
int mid=(tr[node].l+tr[node].r)>>1;
int ans=1e9;
if(l<=mid)
ans=min(ans,querymn(node*2,l,r));
if(r>mid)
ans=min(ans,querymn(node*2+1,l,r));
return ans;
}
bool check(int l,int r)
{
if(a[l]==querymn(1,l,r)&&a[r]==querymx(1,l,r))
return true;
else
return false;
}
int dfs(int l,int r)
{
if(l+1==r) return 1;
if(l>=r) return 0;
int L=pos[querymn(1,l,r)];
int R=pos[querymx(1,l,r)];
if(L>R)
{
int t=L;
L=R;
R=t;
}
return 1+dfs(l,L)+dfs(R,r);
}
void solve()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),pos[a[i]]=i;
if(n==1)
{
printf("0\n");
return ;
}
build(1,1,n);
printf("%d\n",dfs(1,n));
return ;
}
signed main()
{
int t;
cin>>t;
while(t--)
solve();
return 0;
}E. Placing Jinas
Problem - E - Codeforces https://codeforces.com/contest/1696/problem/E
https://codeforces.com/contest/1696/problem/E
很妙的一个组合数学.
题意:给出一个不会增长的数组a,第 i 列在<a[i]的行的格子都是白色.有一个娃娃从(0,0)出发,每次它都也可以向下和向右进行分身.每次分完身,就会拿取分身之前那个格子里面的娃娃.问要把白色格子里的娃娃拿完,共拿了多少娃娃.
思路:这个,每格的娃娃数量就相当于走到当前点的路径数量,是一个很经典的组合数模型,针对于每个点(x,y),可以取到的娃娃数量就是 那么每一列的白色格子上可以取的娃娃格子个数就是
那么每一列的白色格子上可以取的娃娃格子个数就是![\sum_{i=0}^{a[i-1]}(_{a[i]-1}^{a[i]-1+i}\textrm{})](http://img.inotgo.com/imagesLocal/202207/04/202207040834089542_4.gif) 再对每一列进行求和即可,下面是详细的推导过程:
再对每一列进行求和即可,下面是详细的推导过程:

#include<map>
#include<cmath>
#include<set>
#include<queue>
#include<string>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_set>
#include<unordered_map>
#define int long long
const int mod=1e9+7;
using namespace std;
int fact[400005];
int infact[400005];
int a[400005];
int ksm(int x,int y)
{
int res=1;
while(y)
{
if(y&1)
res=res*x%mod;
y>>=1;
x=x*x%mod;
}
return res;
}
void init()
{
fact[0]=1;
infact[0]=1;
for(int i=1;i<=4e5+2;i++)
{
fact[i]=fact[i-1]*i%mod;
infact[i]=infact[i-1]*ksm(i,mod-2)%mod;
}
}
int c(int a,int b)
{
if(a<b)
return 0;
return fact[a]*infact[b]%mod*infact[a-b]%mod;
}
void solve()
{
int n;
cin>>n;
int ans=0;
for(int i=0;i<=n;i++)
{
cin>>a[i];
ans=(ans+c(a[i]+i,i+1))%mod;
}
cout<<ans<<"\n";
return ;
}
signed main()
{
init();
solve();
return 0;
}斗奋力努
边栏推荐
- R language uses cforest function in Party package to build random forest based on conditional inference trees, uses varimp function to check feature importance, and uses table function to calculate co
- R language ggplot2 visualization: ggplot2 visualization grouping box diagram, place the legend and title of the visualization image on the top left of the image and align them to the left, in which th
- How to send pictures to the server in the form of file stream through the upload control of antd
- yolov5 xml数据集转换为VOC数据集
- Use preg_ Match extracts the string into the array between: & | people PHP
- 【性能測試】一文讀懂Jmeter
- Parallel shift does not provide any acceleration - C #
- Leetcode topic [array] -136- numbers that appear only once
- Four essential material websites for we media people to help you easily create popular models
- AcWing 244. Enigmatic cow (tree array + binary search)
猜你喜欢
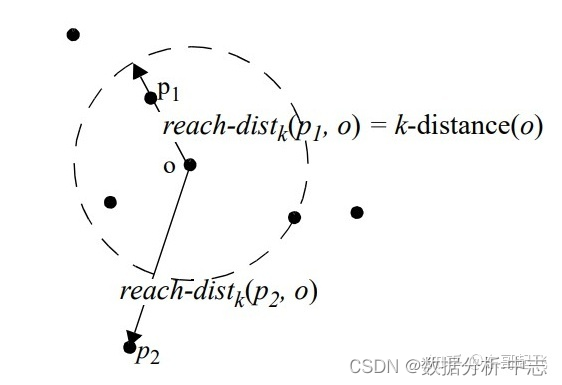
一文了解数据异常值检测方法
![Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 007 - production and setting skybox resources](/img/f9/6c97697896cd1bd0f1d62542959f29.jpg)
Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 007 - production and setting skybox resources
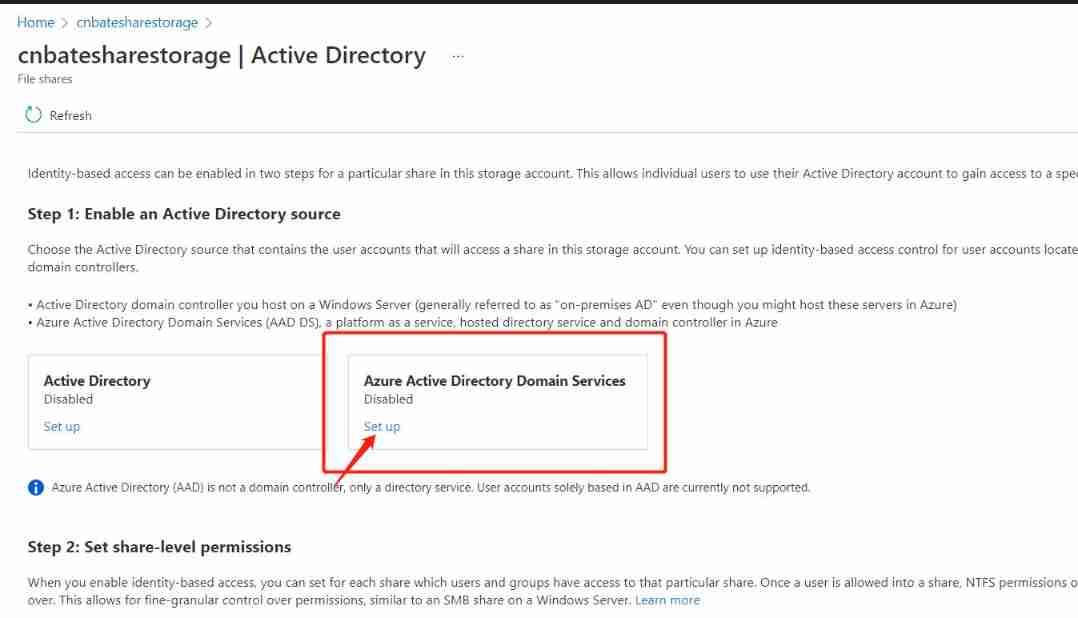
Azure ad domain service (II) configure azure file share disk sharing for machines in the domain service

ES6 summary
根据数字显示中文汉字
![[test de performance] lire jmeter](/img/c9/25a0df681c7ecb4a0a737259c882b3.png)
[test de performance] lire jmeter

Display Chinese characters according to numbers
manjaro安装微信

【Go基础】1 - Go Go Go
没有Kubernetes怎么玩Dapr?
随机推荐
[test de performance] lire jmeter
Collections in Scala
Parallel shift does not provide any acceleration - C #
manjaro安装微信
C#实现一个万物皆可排序的队列
Sort by item from the list within the list - C #
ctfshow web255 web 256 web257
C # implements a queue in which everything can be sorted
How to get bytes containing null terminators from a string- c#
1. Kalman filter - the best linear filter
一文了解数据异常值检测方法
NPM run build error
Group programming ladder race - exercise set l2-002 linked list de duplication
What sparks can applet container technology collide with IOT
How college students choose suitable computers
Add log file to slim frame - PHP
How to re enable local connection when the network of laptop is disabled
Use preg_ Match extracts the string into the array between: & | people PHP
How to solve the problem that computers often flash
The basic syntax of mermaid in typera
 https://codeforces.com/contest/1696/problem/A
https://codeforces.com/contest/1696/problem/A