当前位置:网站首页>[set theory] binary relation (example of binary relation on a | binary relation on a)
[set theory] binary relation (example of binary relation on a | binary relation on a)
2022-07-03 04:27:00 【Programmer community】
List of articles
- One 、 A Upper binary relation
- Two 、 A The number of upper binary relations
- 3、 ... and 、 A Upper binary relation Example ( There are two elements in the set )
- Four 、 A Upper binary relation Example ( There are two elements in the set )
One 、 A Upper binary relation
A
A
A Upper binary relation :
yes
A
×
A
A \times A
A×A Any subset of the Cartesian product
R
R
R yes
A
A
A The binary relationship on
⇔
\Leftrightarrow
⇔
R
⊆
A
×
A
R \subseteq A \times A
R⊆A×A
⇔
\Leftrightarrow
⇔
R
∈
P
(
A
×
A
)
R \in P(A \times A)
R∈P(A×A)
Two 、 A The number of upper binary relations
aggregate
A
A
A The number of elements is
∣
A
∣
=
m
|A| = m
∣A∣=m
A
×
A
A \times A
A×A Cartesian product set in Ordered pair The number of elements is
∣
A
×
A
∣
=
m
2
|A \times A| = m^2
∣A×A∣=m2 individual ;
A
×
A
A \times A
A×A Cartesian product The number of power sets is
∣
P
(
A
×
A
)
∣
=
2
m
2
|P(A \times A)| = 2^{m^2}
∣P(A×A)∣=2m2
A
A
A The number of binary relations on has
2
m
2
2^{m^2}
2m2 individual ;
If
A
A
A There are
1
1
1 Elements ,
A
A
A The binary relation on has
2
1
2
=
2
2^{1^2} = 2
212=2 individual ;
If
A
A
A There are
2
2
2 Elements ,
A
A
A The binary relation on has
2
2
2
=
16
2^{2^2} = 16
222=16 individual ;
If
A
A
A There are
3
3
3 Elements ,
A
A
A The binary relation on has
2
3
2
=
512
2^{3^2} = 512
232=512 individual ;
3、 ... and 、 A Upper binary relation Example ( There are two elements in the set )
B
=
{
b
}
B = \{ b \}
B={ b}
aggregate
B
B
B The number of elements is
∣
B
∣
=
1
|B| = 1
∣B∣=1
B
×
B
B \times B
B×B Cartesian product set in Ordered pair The number of elements is
∣
B
×
B
∣
=
1
2
=
1
|B \times B| = 1^2 = 1
∣B×B∣=12=1 individual ;
B
×
B
B \times B
B×B Cartesian product The number of power sets is
∣
P
(
B
×
B
)
∣
=
2
1
2
=
2
|P(B \times B)| = 2^{1^2} = 2
∣P(B×B)∣=212=2
A
A
A The number of binary relations on has
2
1
2
=
2
2^{1^2} = 2
212=2 individual ;
0
0
0 individual Ordered pair The binary relationship of :
R
1
=
∅
R_1 = \varnothing
R1=∅
1
1
1 individual Ordered pair The binary relationship of :
R
2
=
{
b
,
b
}
R_2 = \{ b , b \}
R2={ b,b}
Four 、 A Upper binary relation Example ( There are two elements in the set )
aggregate
A
=
{
a
1
,
a
2
}
A = \{ a_1 , a_2 \}
A={ a1,a2}
be
A
A
A The binary relation on has
16
16
16 individual ;
A
×
A
A \times A
A×A Cartesian product set The number of ordered pairs in
4
4
4 individual ;
A
×
A
A \times A
A×A Cartesian product set The number of power sets is
2
4
=
16
2^4 = 16
24=16 ;
0
0
0 individual Ordered pair The binary relationship of :
1
1
1 individual
R
1
=
∅
R_1 = \varnothing
R1=∅
1
1
1 individual Ordered pair The binary relationship of :
4
4
4 individual
R
2
=
{
a
1
,
a
1
}
R_2 = \{ a_1 , a_1 \}
R2={ a1,a1}
R
3
=
{
a
1
,
a
2
}
R_3 = \{ a_1 , a_2 \}
R3={ a1,a2}
R
4
=
{
a
2
,
a
1
}
R_4 = \{ a_2 , a_1 \}
R4={ a2,a1}
R
5
=
{
a
2
,
a
2
}
R_5 = \{ a_2 , a_2 \}
R5={ a2,a2}
2
2
2 individual Ordered pair The binary relationship of :
6
6
6 individual
R
6
=
{
{
a
1
,
a
1
}
,
{
a
1
,
a
2
}
}
R_6 = \{ \{ a_1 , a_1 \}, \{ a_1 , a_2 \} \}
R6={ { a1,a1},{ a1,a2}}
R
7
=
{
{
a
1
,
a
1
}
,
{
a
2
,
a
1
}
}
R_7 = \{ \{ a_1 , a_1 \}, \{ a_2 , a_1 \} \}
R7={ { a1,a1},{ a2,a1}}
R
8
=
{
{
a
1
,
a
1
}
,
{
a
2
,
a
2
}
}
R_8 = \{ \{ a_1 , a_1 \}, \{ a_2 , a_2 \} \}
R8={ { a1,a1},{ a2,a2}}
R
9
=
{
{
a
1
,
a
2
}
,
{
a
2
,
a
1
}
}
R_9= \{ \{ a_1 , a_2 \} , \{ a_2 , a_1 \} \}
R9={ { a1,a2},{ a2,a1}}
R
10
=
{
{
a
1
,
a
2
}
,
{
a
2
,
a
2
}
}
R_{10}= \{ \{ a_1 , a_2 \} , \{ a_2 , a_2 \} \}
R10={ { a1,a2},{ a2,a2}}
R
11
=
{
{
a
2
,
a
1
}
,
{
a
2
,
a
2
}
}
R_{11}= \{ \{ a_2 , a_1 \} , \{ a_2 , a_2 \} \}
R11={ { a2,a1},{ a2,a2}}
3
3
3 individual Ordered pair The binary relationship of :
4
4
4 individual
R
12
=
{
{
a
1
,
a
1
}
,
{
a
1
,
a
2
}
,
{
a
2
,
a
1
}
}
R_{12} = \{ \{ a_1 , a_1 \}, \{ a_1 , a_2 \} , \{ a_2 , a_1 \} \}
R12={ { a1,a1},{ a1,a2},{ a2,a1}}
R
13
=
{
{
a
1
,
a
1
}
,
{
a
1
,
a
2
}
,
{
a
2
,
a
2
}
}
R_{13} = \{ \{ a_1 , a_1 \}, \{ a_1 , a_2 \} , \{ a_2 , a_2 \}\}
R13={ { a1,a1},{ a1,a2},{ a2,a2}}
R
14
=
{
{
a
1
,
a
1
}
,
{
a
2
,
a
1
}
,
{
a
2
,
a
2
}
}
R_{14} = \{ \{ a_1 , a_1 \}, \{ a_2 , a_1 \} , \{ a_2 , a_2 \}\}
R14={ { a1,a1},{ a2,a1},{ a2,a2}}
R
15
=
{
{
a
1
,
a
2
}
,
{
a
2
,
a
1
}
,
{
a
2
,
a
2
}
}
R_{15} = \{ \{ a_1 , a_2 \} , \{ a_2 , a_1 \} , \{ a_2 , a_2 \}\}
R15={ { a1,a2},{ a2,a1},{ a2,a2}}
4
4
4 individual Ordered pair The binary relationship of :
1
1
1 individual
R
16
=
{
{
a
1
,
a
1
}
,
{
a
1
,
a
2
}
,
{
a
2
,
a
1
}
,
{
a
2
,
a
2
}
}
R_{16} = \{ \{ a_1 , a_1 \}, \{ a_1 , a_2 \} , \{ a_2 , a_1 \} , \{ a_2 , a_2 \}\}
R16={ { a1,a1},{ a1,a2},{ a2,a1},{ a2,a2}}
边栏推荐
- [fxcg] inflation differences will still lead to the differentiation of monetary policies in various countries
- 类的基础语法
- What are the Bluetooth headsets with good sound quality in 2022? Inventory of four high-quality Bluetooth headsets
- X-ray normal based contour rendering
- Small program animation realizes the running lantern and animation object
- 金仓数据库KingbaseES 插件kdb_database_link
- Priv-app permission异常
- GFS distributed file system (it's nice to meet it alone)
- Joint set search: merge intervals and ask whether two numbers are in the same set
- How to connect WiFi with raspberry pie
猜你喜欢
Daily question - ugly number

Function introduction of member points mall system
Why should programmers learn microservice architecture if they want to enter a large factory?

Bugku CTF daily question baby_ flag. txt
Web - Information Collection

Golang -- realize file transfer
一名外包仔的2022年中总结

Prefix and (continuously updated)

Busycal latest Chinese version
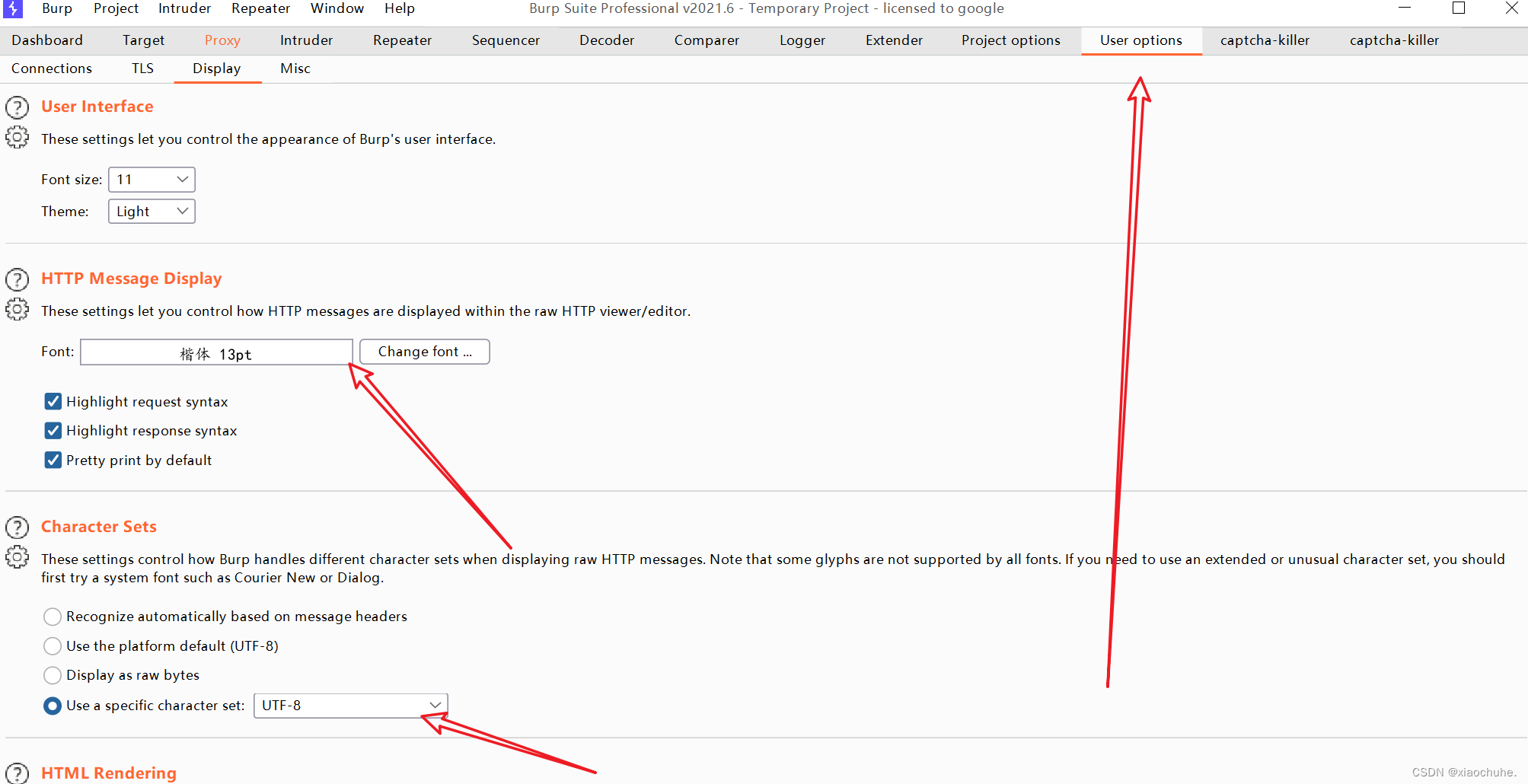
Solve BP Chinese garbled code
随机推荐
Square root of X
[set theory] set concept and relationship (set family | set family examples | multiple sets)
GFS分布式文件系统(光是遇见已经很美好了)
[no title] 2022 chlorination process examination content and free chlorination process examination questions
BMZCTF simple_ pop
FFMpeg example
Export of zip file
How do you use lodash linking function- How do you chain functions using lodash?
Priv app permission exception
[free completion] development of course guidance platform (source code +lunwen)
Web - Information Collection
Mongodb slow query optimization analysis strategy
Basic use of continuous integration server Jenkins
vulnhub HA: Natraj
Ffmpeg tanscoding transcoding
[set theory] set concept and relationship (true subset | empty set | complete set | power set | number of set elements | power set steps)
Joint search set: the number of points in connected blocks (the number of points in a set)
Fcpx template: sweet memory electronic photo album photo display animation beautiful memory
Database management tool, querious direct download
Supervised pre training! Another exploration of text generation!