Leetcode-106: construct a binary tree according to the sequence of middle and later traversal

1. Title Description

Given two arrays of integers inorder and postorder , among inorder Is the middle order traversal of a binary tree , postorder Is the post order traversal of the same tree , Please construct and return this Binary tree .

link ：https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal
Example 1：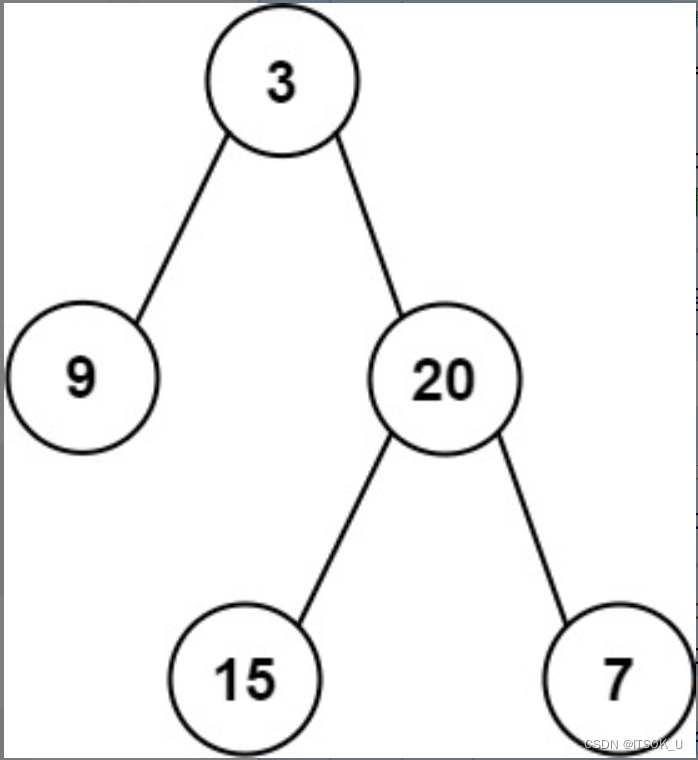

inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
Output ：[3,9,20,null,null,15,7]

Example 2：

Input ：inorder = [-1], postorder = [-1]
Output ：[-1]

2. Problem analysis and solution

2.1 recursive

2.1.1 Recursive thinking

This problem is similar to the previous 105. Construction of binary trees from traversal sequences of preorder and middle order The solution is basically the same , So we can simulate the recursive implementation of the previous problem to solve this problem . In this process, the grasp of subscript changes can be assisted by writing a sequence by yourself , It's easy to understand .

Take the traversal result of the following tree as an example , We can still determine the root node according to the last value of post order traversal , Then, in the middle order traversal, the middle order sequence is divided into left and right parts according to this root node , Node clusters of left and right subtrees as root nodes respectively . According to this idea, we can realize the following recursive process .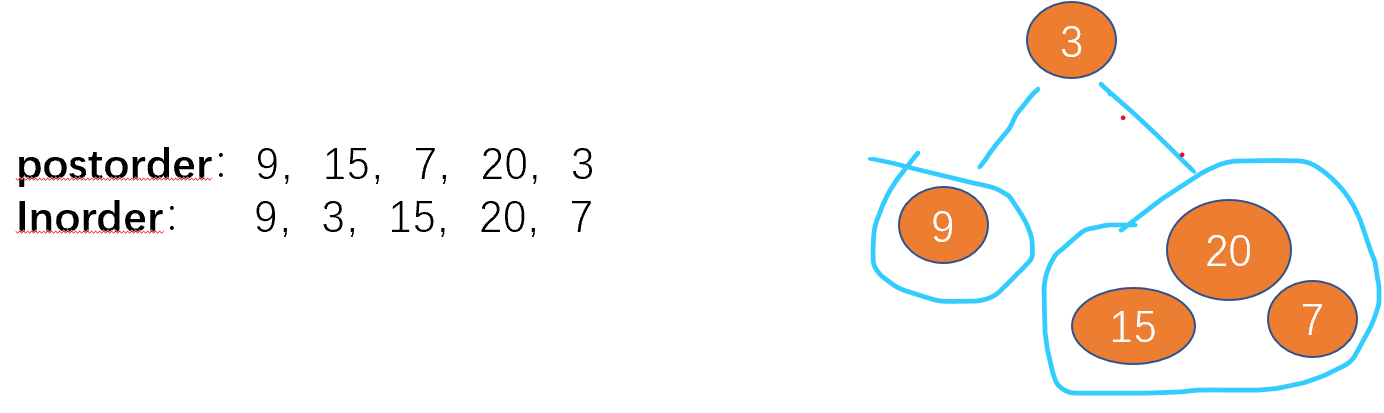

2.1.2 Recursive code （O(N),O(N)）

class Solution {
    
    //  The relation between the node value and the subscript value of the tree in the preorder traversal map mapping 
    unordered_map<int,int> index;
public:
TreeNode* build(vector<int>& inorder,vector<int>& postorder,int inLeft,int inRight,int postLeft,int postRight){
    
        //  The traversal list is empty and returns an empty tree 
        if(inLeft>inRight){
    
            return nullptr;
        }
        //  Record the root node of the tree in post order traversal and the root node of the tree in mid order traversal 
        int postRoot = postRight;
        int inorderRoot = index[postorder[postRoot]];
        //  Construct a tree with only root nodes 
        TreeNode* root = new TreeNode(postorder[postRoot]);
        //  Determine the number of nodes of the left subtree of the tree 
        int leftSize = inorderRoot - inLeft;    
        // Construct the left subtree 
        root->left = build(inorder,postorder,inLeft,inorderRoot-1,postLeft,postLeft+leftSize-1);
        // Construct the right subtree 
        root->right = build(inorder,postorder,inorderRoot+1,inRight,postLeft+leftSize,postRoot-1);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    
        
        size_t size = postorder.size();
        for(int i=0;i<size;i++){
    
            index[inorder[i]] = i;
        }
        if(size == 0) return nullptr;
        return build(inorder,postorder,0,size-1,0,size-1);
    }
};

2.1.3 Recursive code 2（O(N),O(N)）

class Solution {
    
    //  Record the root node in the post order traversal 
    int postIndex;
    //  The relation between the node value and the subscript value of the tree in the preorder traversal map mapping 
    unordered_map<int,int> index;
public:
TreeNode* build(vector<int>& inorder,vector<int>& postorder,int inLeft,int inRight) {
    
        //  The traversal list is empty and returns an empty tree 
        if(inLeft>inRight)  return nullptr;
        //  Record the current root node value 
        int rootVal = postorder[postIndex];
        //  Build a tree with only root nodes 
        TreeNode* root = new TreeNode(rootVal);
        //  Find the subscript value of the root node in the middle order traversal 
        int rootIndex = index[rootVal];
        //  After traversing the root node, the subscript minus one shifts left 
        postIndex--;
        //  Build the right subtree , Note that the right subtree must be constructed first ,
        //  Otherwise, when building the left subtree postIndex-- Will move incorrectly 
        //  Due to the traversal order , The elements closest to the left of the root node in the subsequent order are all in the right subtree 
        root->right = build(inorder,postorder,rootIndex+1,inRight);
        //  Build the left subtree 
        root->left = build(inorder,postorder,inLeft,rootIndex-1);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    
        
        size_t size = postorder.size();
        postIndex = size -1;

        for(int i=0;i<size;i++){
    
            index[inorder[i]] = i;
        }
        if(size == 0) return nullptr;
        return build(inorder,postorder,0,size-1);
    }
};

2.2 iteration

Iteration is also the same as before 105. Construction of binary trees from traversal sequences of preorder and middle order Basically the same , We analyze the relationship between nodes in post order traversal . Suppose there are two adjacent nodes in the post order traversal sequence u and v, Then there are only two situations in their relationship ：

• u yes v The right child
• u yes v The left child of an ancestor of

in other words , as long as u yes v The children of , That must be the right child , Otherwise, it cannot be u The children of . This is related to the post order traversal order of binary tree , Because the order of post order traversal is the left child - The right child - root , The relationship between seats and adjacent nodes can only be one of the above two .
Therefore, we can realize the logic of iteration according to this .

But how can we determine which of the two cases is in the solution process , This requires the help of middle order traversal . For middle order traversal , The first node value must be the leftmost node value of the current tree , The last node value must be the rightmost node value of the current tree . Let's continue to look at a tree below

Move the traversal sequence of the middle order traversal from back to front , We'll find out , Each node is the rightmost node of the tree after removing all subsequent nodes . We know that if a node is the rightmost node , Then he has no left child . Knowing this, we can use this to determine the situation of the newly added node .

• If the newly added node is on the rightmost side of the current sequence traversal , Then the next node must not be a right child
• If the newly added node is not on the far right of the current sequence , Then the next node is still a right child .

So we can maintain a stack to save all nodes without adding left children so that we can add right children later , adopt inorderIndex To mark the tree maintained by the current sequence . The specific code is as follows ：

class Solution {
    
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    
        size_t size = postorder.size();
        //  Empty tree 
        if(size == 0)   return nullptr;
        //  With size Record the subscript value of sequential access 
        size--;
        //  Construct a tree with only root nodes 
        TreeNode* root = new TreeNode(postorder[size]);
        stack<TreeNode*> st;
        //  Root node stack 
        st.push(root);
        //  Middle order access subscript 
        int  inorderIndex = size;
        //  Handle nodes other than the root node 
        while(size--){
    
            //  Take the newly accessed post order to traverse the node （ From back to front ）
            int postVal = postorder[size];
            //  Take the top node of the stack 
            TreeNode* node = st.top();
            //  The new node is the right child of the top node of the stack 
            if(node->val != inorder[inorderIndex]){
    
                node->right = new TreeNode(postVal);
                st.push(node->right);
            }else{
    
                //  The new node is not the child of the top node 
                //  That is the left child of an ancestor at the top of the stack 
                while(!st.empty() && st.top()->val == inorder[inorderIndex]){
    
                    node = st.top();
                    st.pop();
                    --inorderIndex;
                }
                node->left = new TreeNode(postVal);
                st.push(node->left);
            }
        }
        return root;
    }
};

summary ： Recursively solving binary tree correlation is relatively easy to understand