当前位置:网站首页>Leetcode-112:路径总和
Leetcode-112:路径总和
2022-07-03 09:22:00 【ITSOK_U】
112. 路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。
如果存在,返回 true ;否则,返回 false 。叶子节点是指没有子节点的节点。
这道题和题257. 二叉树的所有路径十分类似,代码也相似。
深度优先(O(N),O(N))
在本题使用深度优先的话可以使用前序递归来模拟实现,但是在递归中需要处理的是每个节点的路径和的计算要确保不对其它的节点路径和计算造成影响,所以使用递归的话在其回溯过程会需要处理那些多余的叶节点。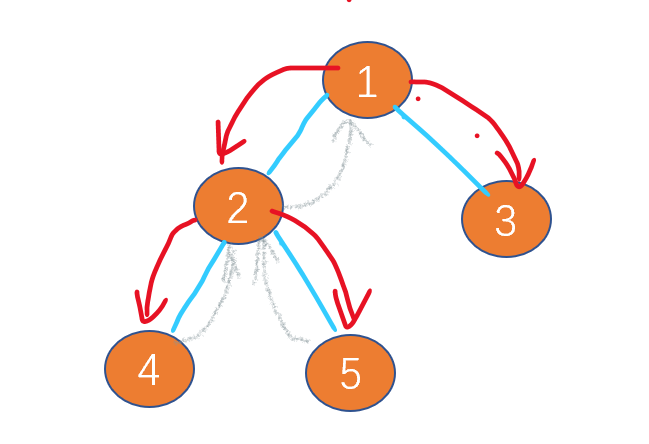
如在上述的路径和计算中,第一条叶子节点的路径和计算为1+2+4,如果此时不满足要求,则需要进行回溯,所以要更新已有结果为1+2,使用递归的话可以完美的解决这种问题,如下面代码中的return就可以实现有效的回溯。
if(root->left == nullptr && root->right == nullptr){
if(num == target) falg = true;
// 否则继续递归
return;
}
具体解题代码如下:
class Solution {
public:
void findPath(TreeNode* root,int num,int target,bool &falg){
// 新加入了节点更新路径和
num += root->val;
// 到达叶子节点
if(root->left == nullptr && root->right == nullptr){
// 满足求解条件,结果标志为真
if(num == target){
falg = true;
}
// 否则继续递归
return;
}
// 左子树递归
if(root->left) findPath(root->left,num,target,falg);
// 右子树递归
if(root->right) findPath(root->right,num,target,falg);
}
bool hasPathSum(TreeNode* root, int targetSum) {
// 根节点为空,返回false
if(root == nullptr) return false;
// falg用来标记求解结果
bool falg = false;
findPath(root,0,targetSum,falg);
return falg;
}
};
广度优先(O(N),O(N))
使用广度优先的话就是模拟一次层序遍历。不过相比于普通的打印路径之类的求解,此时我们需要维护一个各个节点已有的路径和队列。如下图所示。我们的路径和队列是和树节点队列一一位置对应的,也就是说,与树节点队列相同位置的路径和队列的值就是到该树节点的路径和。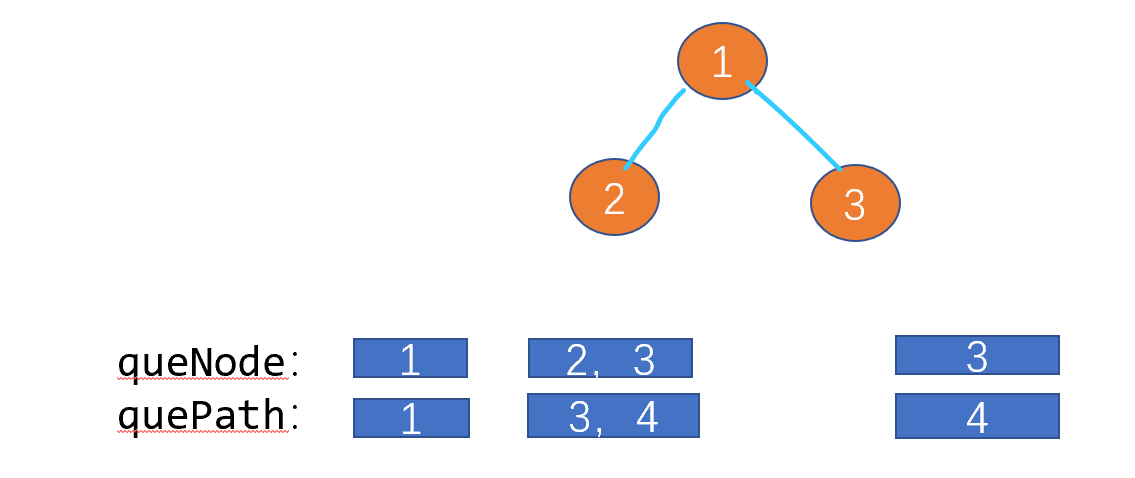
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
// 空树直接返回false
if(root == nullptr) return false;
// 初始化广度遍历的树节点队列
queue<TreeNode*> que;
queue<int> num;
que.push(root);
num.push(root->val);
// 队列不为空则节点未处理完
while(!que.empty()){
// 取出树节点队列以及路径和队列的首元素
TreeNode* node = que.front();
int res=num.front();
que.pop();
num.pop();
// 如果到了叶子节点而且路径和满足要求则直接跳出遍历,返回true
if(node->left==nullptr && node->right==nullptr && res==targetSum)
return true;
if(node->left){
que.push(node->left);
// 下一层节点入队,并将其对应的节点路径和存储
num.push(node->left->val + res);
}
if(node->right){
que.push(node->right);
// 下一层节点入队,并将其对应的节点路径和存储
num.push(node->right->val + res);
}
}
// 节点处理完仍然没有找到加和为targetSum的路径,返回false
return false;
}
};
边栏推荐
- Opencv Harris corner detection
- LeetCode - 508. 出现次数最多的子树元素和 (二叉树的遍历)
- CV learning notes - Stereo Vision (point cloud model, spin image, 3D reconstruction)
- Swing transformer details-2
- The underlying principle of vector
- Windows下MySQL的安装和删除
- Opencv gray histogram, histogram specification
- is_ power_ of_ 2 judge whether it is a multiple of 2
- Drive and control program of Dianchuan charging board for charging pile design
- After clicking the Save button, you can only click it once
猜你喜欢
Crash工具基本使用及实战分享

LeetCode 面试题 17.20. 连续中值(大顶堆+小顶堆)

2. Elment UI date selector formatting problem

Opencv note 21 frequency domain filtering

2021-10-28

2.1 Dynamic programming and case study: Jack‘s car rental
ADS simulation design of class AB RF power amplifier

Not many people can finally bring their interests to college graduation
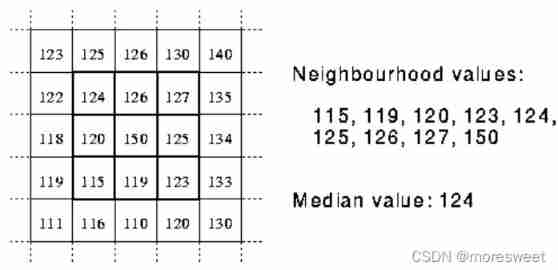
CV learning notes - image filter
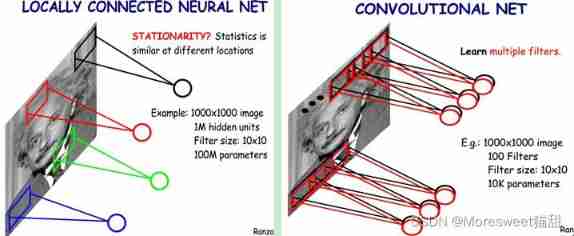
CV learning notes convolutional neural network
随机推荐
LeetCode 面试题 17.20. 连续中值(大顶堆+小顶堆)
el-table X轴方向(横向)滚动条默认滑到右边
03 FastJson 解决循环引用
2021-01-03
[combinatorics] combinatorial existence theorem (three combinatorial existence theorems | finite poset decomposition theorem | Ramsey theorem | existence theorem of different representative systems |
My 4G smart charging pile gateway design and development related articles
CV learning notes - feature extraction
03 fastjason solves circular references
Opencv note 21 frequency domain filtering
Positive and negative sample division and architecture understanding in image classification and target detection
[keil5 debugging] warning:enumerated type mixed with other type
4G module initialization of charge point design
CV learning notes - BP neural network training example (including detailed calculation process and formula derivation)
Vgg16 migration learning source code
Leetcode bit operation
Opencv image rotation
Toolbutton property settings
pycharm 无法引入自定义包
Opencv feature extraction sift
Leetcode interview question 17.20 Continuous median (large top pile + small top pile)