当前位置:网站首页>Some properties of leetcode139 Yang Hui triangle
Some properties of leetcode139 Yang Hui triangle
2022-07-07 10:22:00 【qq_ forty-two million one hundred and twenty thousand eight hun】
Yang Hui triangle has special properties
- Each line of numbers is symmetrical from 1 Start getting bigger and smaller , And finally back to 1.
- The first n That's ok ( from 0 open beginning Ed Number ) Count word Yes n + 1 term , front n That's ok common Yes n ( n + 1 ) 2 individual Count The first n That's ok ( from 0 Numbered starting ) The numbers are n+1 term , front n All lines have \frac{n(n+1)}{2} Number The first n That's ok ( from 0 open beginning Ed Number ) Count word Yes n+1 term , front n That's ok common Yes 2n(n+1) individual Count
- The first n That's ok Of The first m individual Count ( from 0 open beginning Ed Number ) can surface in by Group close Count C n m = n ! m ! ( n − m ) ! The first n OK, No m Number ( from 0 Numbered starting ) Can be expressed as a combined number \mathrm{C}_n^m = \frac{n!}{m!(n-m)!} The first n That's ok Of The first m individual Count ( from 0 open beginning Ed Number ) can surface in by Group close Count Cnm=m!(n−m)!n!
- Each number is equal to the sum of the left and right numbers in the previous line
- ( a + b ) n Of exhibition open type ( Two term type exhibition open ) in Of various term system Count In accordance with the Time Yes Should be Yang Brightness 3、 ... and horn The first n That's ok in Of Every time One term ( Such as : ( a + b ) 2 = a 2 + 2 a b + b 2 ) \ (a+b)^n The expansion of ( Binomial expansion ) The coefficients in correspond to Yang Hui triangle n Each item in the line ( Such as : \ (a+b)^2 = a^2 + 2ab + b^2) (a+b)n Of exhibition open type ( Two term type exhibition open ) in Of various term system Count In accordance with the Time Yes Should be Yang Brightness 3、 ... and horn The first n That's ok in Of Every time One term ( Such as : (a+b)2=a2+2ab+b2)

边栏推荐
- ES类和对象、原型
- 2022.7.5DAY597
- 2022.7.3DAY595
- The request object parses the request body and request header parameters
- Chris Lattner, père de llvm: Pourquoi reconstruire le logiciel d'infrastructure ai
- 大整数类实现阶乘
- Easyexcel read write simple to use
- Postman tutorial - scripting
- MCU is the most popular science (ten thousand words summary, worth collecting)
- UnityWebRequest基础使用之下载文本、图片、AB包
猜你喜欢
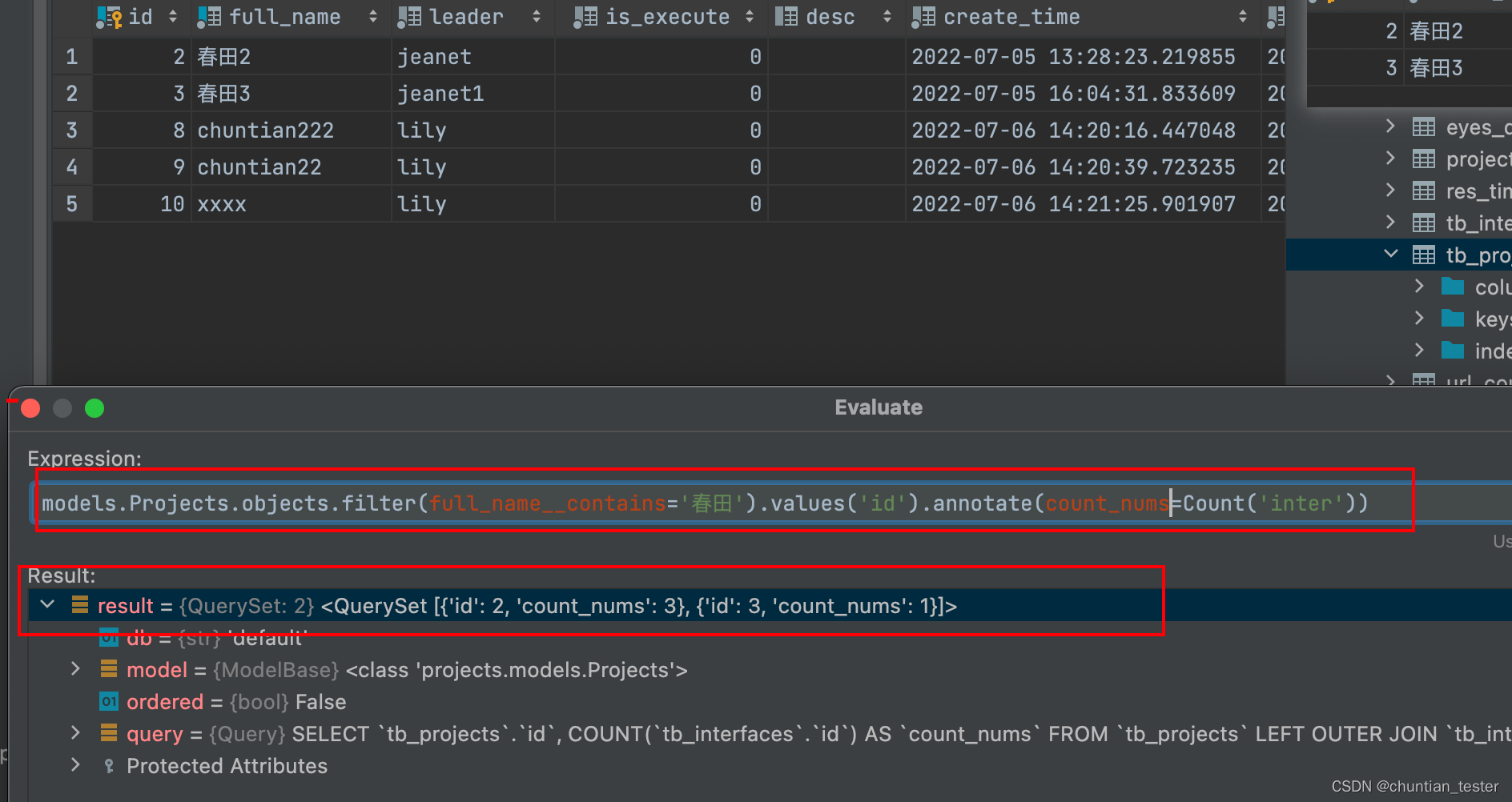
ORM -- grouping query, aggregation query, query set queryset object properties

JMeter installation
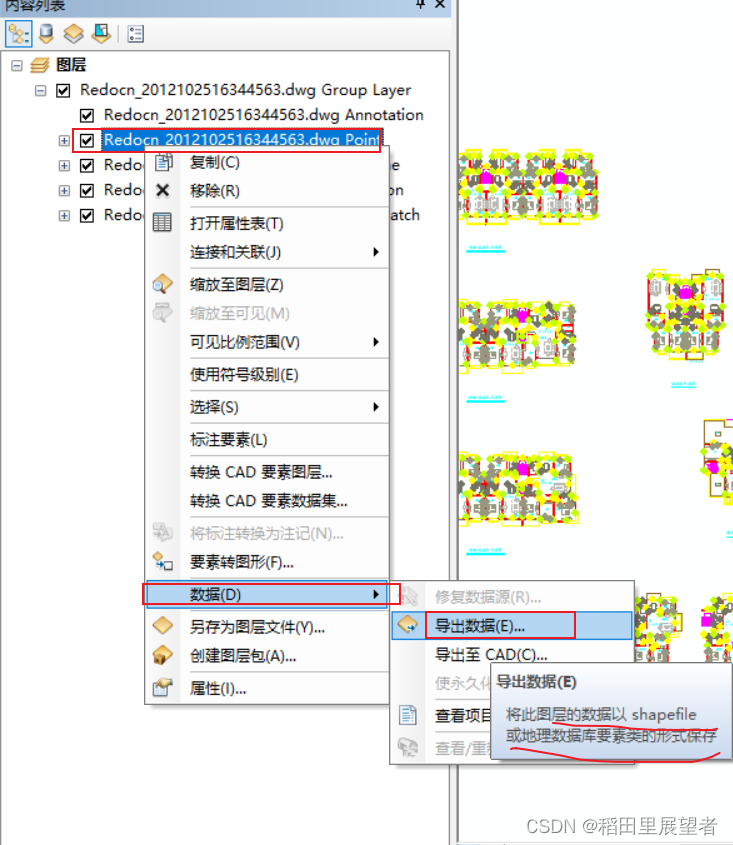
ArcGIS operation: converting DWG data to SHP data

LLVM之父Chris Lattner:為什麼我們要重建AI基礎設施軟件
![[learning notes - Li Hongyi] Gan (generation of confrontation network) full series (I)](/img/94/b4df1ce2861a851fcd8de3e08540b0.png)
[learning notes - Li Hongyi] Gan (generation of confrontation network) full series (I)
【STM32】STM32烧录程序后SWD无法识别器件的问题解决方法

一文讲解单片机、ARM、MUC、DSP、FPGA、嵌入式错综复杂的关系
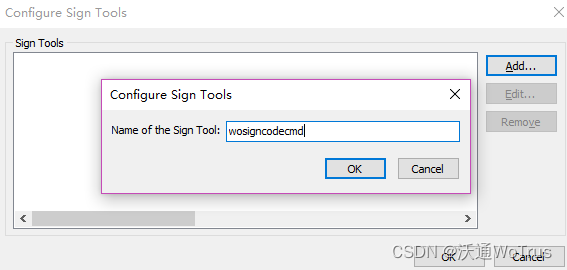
Inno setup packaging and signing Guide

Guide de signature du Code Appx
STM32基础知识—内存映射
随机推荐
【ORM框架】
字符串格式化
Enterprise practice | construction of banking operation and maintenance index system under complex business relations
对存储过程进行加密和解密(SQL 2008/SQL 2012)
CONDA creates virtual environment offline
ORM -- query type, association query
一文讲解单片机、ARM、MUC、DSP、FPGA、嵌入式错综复杂的关系
虚数j的物理意义
STM32中AHB总线_APB2总线_APB1总线这些是什么
STM32 ADC and DMA
Appx代码签名指南
ORM -- database addition, deletion, modification and query operation logic
Postman interface test VII
JMeter installation
Download Text, pictures and ab packages used by unitywebrequest Foundation
Finally, there is no need to change a line of code! Shardingsphere native driver comes out
[ORM framework]
IPv4 socket address structure
Some test points about coupon test
2022.7.6DAY598