当前位置:网站首页>[combinatorics] exponential generating function (proving that the exponential generating function solves the arrangement of multiple sets)
[combinatorics] exponential generating function (proving that the exponential generating function solves the arrangement of multiple sets)
2022-07-03 18:18:00 【Programmer community】
List of articles
- One 、 Prove that the exponential generating function solves the arrangement of multiple sets
Reference blog : Look in order
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
- 【 Combinatorial mathematics 】 Generating function ( Use the generating function to solve multiple sets r Combinatorial number )
- 【 Combinatorial mathematics 】 Generating function ( Use generating function to solve the number of solutions of indefinite equation )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations )
- 【 Combinatorial mathematics 】 Generating function ( Examples of using generating functions to solve the number of solutions of indefinite equations 2 | Extended to integer solutions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | disorder | Orderly | Allow repetition | No repetition | Unordered and unrepeated splitting | Unordered repeated split )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Unordered non repeated split example )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Basic model of positive integer splitting | Disorderly splitting with restrictions )
- 【 Combinatorial mathematics 】 Generating function ( Positive integer split | Repeated ordered splitting | Do not repeat orderly splitting | Proof of the number of repeated ordered splitting schemes )
- 【 Combinatorial mathematics 】 Exponential generating function ( The concept of exponential generating function | Permutation number exponential generating function = General generating function of combinatorial number | Example of exponential generating function )
One 、 Prove that the exponential generating function solves the arrangement of multiple sets
Multiple sets
S
=
{
n
1
⋅
a
1
,
n
2
⋅
a
2
,
⋯
,
n
k
⋅
a
k
}
S=\{ n_1 \cdot a_1 , n_2 \cdot a_2 , \cdots , n_k \cdot a_k \}
S={ n1⋅a1,n2⋅a2,⋯,nk⋅ak}
Multiple sets
S
S
S Of
r
r
r Number of permutations Composition sequence
{
a
r
}
\{ a_r \}
{ ar} , The corresponding exponential generating function is :
G
e
(
x
)
=
f
n
1
(
x
)
f
n
2
(
x
)
⋯
f
n
k
(
x
)
G_e(x) = f_{n_1}(x) f_{n_2}(x) \cdots f_{n_k}(x)
Ge(x)=fn1(x)fn2(x)⋯fnk(x) *
Each generated function item
f
n
i
(
x
)
f_{n_i}(x)
fni(x) yes
f
n
i
(
x
)
=
1
+
x
+
x
2
2
!
+
⋯
+
x
n
i
n
i
!
f_{n_i}(x) = 1 + x + \cfrac{x^2}{2!} + \cdots + \cfrac{x^{n_i}}{n_i!}
fni(x)=1+x+2!x2+⋯+ni!xni *
take
G
e
(
x
)
G_e(x)
Ge(x) an , Among them
r
r
r The coefficient is the permutation number of multiple sets ; *
Prove the purpose of the above exponential generating function :
Put the above Exponential generating function an ,
Exponential generating function term
G
e
(
x
)
=
f
n
1
(
x
)
f
n
2
(
x
)
⋯
f
n
k
(
x
)
G_e(x) = f_{n_1}(x) f_{n_2}(x) \cdots f_{n_k}(x)
Ge(x)=fn1(x)fn2(x)⋯fnk(x) , from
k
k
k Multiply the factors to get ,
Each factor will provide a
x
m
1
m
1
!
\cfrac{x^{m_1}}{m_1!}
m1!xm1 composition ,
x
m
1
m
1
!
\cfrac{x^{m_1}}{m_1!}
m1!xm1 From the first factor ,
x
m
2
m
2
!
\cfrac{x^{m_2}}{m_2!}
m2!xm2 From the second factor ,
⋮
\vdots
⋮
x
m
k
m
k
!
\cfrac{x^{m_k}}{m_k!}
mk!xmk From
k
k
k Personal factor ,
Multiply the above factors
x
m
1
m
1
!
⋅
x
m
2
m
2
!
⋯
x
m
k
m
k
!
\cfrac{x^{m_1}}{m_1!} \cdot \cfrac{x^{m_2}}{m_2!} \cdots \cfrac{x^{m_k}}{m_k!}
m1!xm1⋅m2!xm2⋯mk!xmk
among
m
1
+
m
2
+
⋯
+
m
r
=
r
,
m_1 + m_2 + \cdots + m_r = r \ \ \ ,
m1+m2+⋯+mr=r ,
0
≤
m
i
≤
n
i
,
0 \leq m_i \leq n_i \ \ ,
0≤mi≤ni ,
i
=
0
,
1
,
2
,
⋯
,
k
i= 0,1,2, \cdots , k
i=0,1,2,⋯,k
x
m
1
m
1
!
⋅
x
m
2
m
2
!
⋯
x
m
k
m
k
!
\cfrac{x^{m_1}}{m_1!} \cdot \cfrac{x^{m_2}}{m_2!} \cdots \cfrac{x^{m_k}}{m_k!}
m1!xm1⋅m2!xm2⋯mk!xmk Corresponding to the subitem after the expansion of the exponential generating function ;
x
m
1
m
1
!
⋅
x
m
2
m
2
!
⋯
x
m
k
m
k
!
\ \ \ \ \cfrac{x^{m_1}}{m_1!} \cdot \cfrac{x^{m_2}}{m_2!} \cdots \cfrac{x^{m_k}}{m_k!}
m1!xm1⋅m2!xm2⋯mk!xmk
=
x
m
1
+
m
2
+
⋯
+
m
k
m
1
!
m
2
!
⋯
m
k
!
=\cfrac{x^{m_1 + m_2 + \cdots + m_k}}{m_1!m_2!\cdots m_k!}
=m1!m2!⋯mk!xm1+m2+⋯+mk
=
x
r
m
1
!
m
2
!
⋯
m
k
!
⋅
r
!
r
!
=\cfrac{x^{r}}{m_1!m_2!\cdots m_k!} \cdot \cfrac{r!}{r!}
=m1!m2!⋯mk!xr⋅r!r!
=
x
r
r
!
⋅
r
!
m
1
!
m
2
!
⋯
m
k
!
=\cfrac{x^{r}}{r!} \cdot \cfrac{r!}{m_1!m_2!\cdots m_k!}
=r!xr⋅m1!m2!⋯mk!r!
r
!
m
1
!
m
2
!
⋯
m
k
!
\cfrac{r!}{m_1!m_2!\cdots m_k!}
m1!m2!⋯mk!r! Is a multiple set
r
r
r The total number of permutations of elements
Yes
r
r
r Elements , The number of methods selected is
m
1
+
m
2
+
⋯
+
m
r
=
r
m_1 + m_2 + \cdots + m_r = r
m1+m2+⋯+mr=r Number of nonnegative integer solutions , When the configuration is complete , Again Make a full arrangement , You can get
r
r
r array ;
( First choose , And then we'll do a full permutation )
a
r
=
∑
r
!
m
1
!
m
2
!
⋯
m
k
!
a_r = \sum\cfrac{r!}{m_1!m_2!\cdots m_k!}
ar=∑m1!m2!⋯mk!r!
Sum above , Each item is satisfied
m
1
+
m
2
+
⋯
+
m
r
=
r
m_1 + m_2 + \cdots + m_r = r
m1+m2+⋯+mr=r Nonnegative integer solution of the equation , Each nonnegative integer solution corresponds to the
S
S
S Of
r
r
r Combine ;
The total permutation of the combination is
r
!
m
1
!
m
2
!
⋯
m
k
!
\cfrac{r!}{m_1!m_2!\cdots m_k!}
m1!m2!⋯mk!r! ,
Sum above
a
r
=
∑
r
!
m
1
!
m
2
!
⋯
m
k
!
a_r = \sum\cfrac{r!}{m_1!m_2!\cdots m_k!}
ar=∑m1!m2!⋯mk!r! yes Sum all nonnegative integer solutions that satisfy the equation ;
边栏推荐
- A. Berland Poker & 1000 [simple mathematical thinking]
- Computer graduation design PHP makeup sales Beauty shopping mall
- PHP MySQL create database
- What kind of experience is it when the Institute earns 20000 yuan a month?
- Ml (machine learning) softmax function to realize the classification of simple movie categories
- OpenSSL的SSL/BIO_get_fd
- Investigation on the operation prospect of the global and Chinese Anti enkephalinase market and analysis report on the investment strategy of the 14th five year plan 2022-2028
- 小程序 多tab 多swiper + 每个tab分页
- 网格图中递增路径的数目[dfs逆向路径+记忆dfs]
- 聊聊支付流程的设计与实现逻辑
猜你喜欢

Sensor 调试流程

Valentine's day, send you a little red flower~
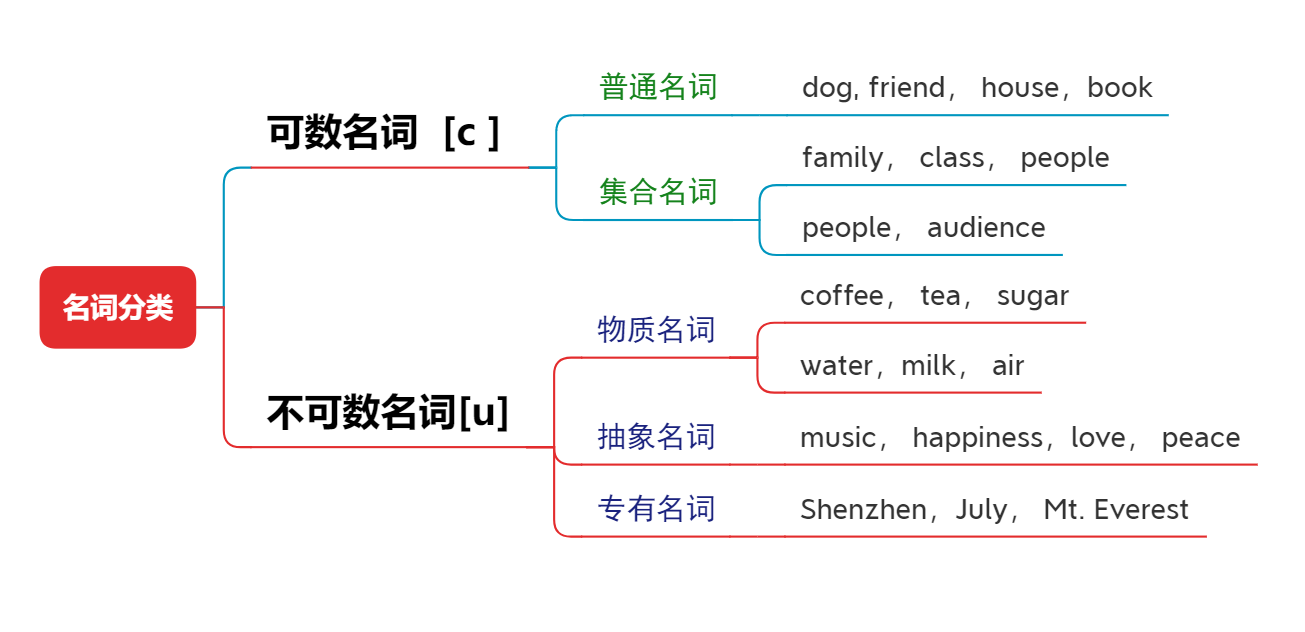
English語法_名詞 - 分類

Ml (machine learning) softmax function to realize the classification of simple movie categories

Global and Chinese pediatric palliative care drug market development research and investment planning recommendations report 2022-2028
![Lesson 13 of the Blue Bridge Cup -- tree array and line segment tree [exercise]](/img/da/0a282b4773fe3909d1e5e9d19f8549.jpg)
Lesson 13 of the Blue Bridge Cup -- tree array and line segment tree [exercise]
On Data Mining
![AcWing 271. Teacher Yang's photographic arrangement [multidimensional DP]](/img/3d/6d61fefc62063596221f98999a863b.png)
AcWing 271. Teacher Yang's photographic arrangement [multidimensional DP]

Interviewer: why is the value nil not equal to nil?

2022-2028 global petroleum pipe joint industry research and trend analysis report
随机推荐
Talk about the design and implementation logic of payment process
Closure and closure function
小程序 多tab 多swiper + 每个tab分页
Five problems of database operation in commodity supermarket system
(8) HS corner detection
How to install PHP on Ubuntu 20.04
MySQL has been stopped in the configuration interface during installation
模块九作业
Market demand survey and marketing strategy analysis report of global and Chinese pet milk substitutes 2022-2028
Getting started with deops
Golang string (string) and byte array ([]byte) are converted to each other
[combinatorics] generating function (use generating function to solve the number of solutions of indefinite equation example 2 | extended to integer solution)
Computer graduation design PHP makeup sales Beauty shopping mall
Redis core technology and practice - learning notes (VI) how to achieve data consistency between master and slave Libraries
What kind of experience is it when the Institute earns 20000 yuan a month?
网格图中递增路径的数目[dfs逆向路径+记忆dfs]
[linux]centos 7 reports an error when installing MySQL "no package MySQL server available" no package ZABBIX server MySQL available
Talk about the design and implementation logic of payment process
Theoretical description of linear equations and summary of methods for solving linear equations by eigen
How do microservices aggregate API documents? This wave of operation is too good