Differential (one-dimensional, two-dimensional, three-dimensional) Blue Bridge Cup three body attack

If one dimension and two dimensions are OK, you can jump directly

• Three dimensional difference

One dimensional difference

First, give an original array a：a[1], a[2], a[3], a[n];
Then we construct an array b ： b[1] ,b[2] , b[3], b[i];
bring a[i] = b[1] + b[2 ]+ b[3] +, + b[i]

a An array is b Array prefix and array , In turn, we put b The array is called a Differential array of arrays .

Consider constructive difference b Array
The most direct way
as follows ：
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
…
b[n] = a[n] - a[n-1];
Yes b Array , By prefix and operation , You can go to O(n) Get... In time a Array .

One dimensional difference —— The template questions AcWing 797. Difference
Give interval [l, r] Add to each number in c：b[l] += c, b[r + 1] -= c
Example
AcWing797. Difference
Enter a length of n Integer sequence of . Next input m Operations , Each operation contains three integers l,r,c, Indicates that... Will be in the sequence [l,r] Add... To each number between c.
Please output the sequence after all operations .

Input format
The first line contains two integers n and m.
The second line contains n It's an integer , Represents a sequence of integers .
Next m That's ok , Each line contains three integers l,r,c, Represents an operation .

Output format
All in one line , contain n It's an integer , Represents the final sequence .

Data range
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤ The value of an element in an integer sequence ≤1000
sample input ：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
sample output ：
3 4 5 3 4 2

#include<bits/stdc+. and >
using namespace std;
const int N=1e5+10;
int a[N],b[N]; 
int main()
{
     
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) 
    {
    
        scanf("%d",&a[i]);
        b[i]=a[i]-a[i-1];      // Build a differential array 
    }
    int l,r,c;
    while(m--)
    {
    
        scanf("%d%d%d",&l,&r,&c);
        b[l]+=c;     // Put... In the sequence [l, r] Add... To every number between c
        b[r+1]-=c;
    }
    for(int i=1;i<=n;i++) 
    {
    
        a[i]=b[i]+a[i-1];    // Prefixes and operations 
        printf("%d ",a[i]);
    }
    return 0;
}

Two dimensional difference

author ：z When the forest is deep, see the deer
If extended to 2D , We need to add... To the value of each element in the selected submatrix of the two-dimensional array c, Whether it can also achieve O(1) Time complexity of . The answer is yes , Consider two-dimensional difference .

a[][] An array is b[][] Array prefix and array , that b[][] yes a[][] The differential array of
Original array ： a[i][j]
Let's construct a differential array ： b[i][j]
bring a Array a[i][j] yes b The upper left corner of the array (1,1) To the lower right corner (i,j) The sum of the elements of the enclosed rectangle .

How to construct b Array? ？

Let's think backwards .

Same as one-dimensional difference , We construct a two-dimensional difference fraction group to Let the original two-dimensional array a Add... To each element in the selected neutron matrix c The operation of , Can be O(n*n) The time complexity is optimized to O(1)

Known original array a The selected submatrix in is With (x1,y1) It's the upper left corner , With (x2,y2) Is the rectangular area enclosed by the lower right corner ;

Always remember ,a An array is b Array prefix and array , For example, yes. b Array of b[i][j] Modification of , Will affect a Array from a[i][j] And every number from now on .

Suppose we have constructed b Array , Analogy to one-dimensional difference , We do the following
Add... To the value of each element in the selected submatrix c Time complexity o(1)

b[x1][y1] + = c;

b[x1,][y2+1] - = c;

b[x2+1][y1] - = c;

b[x2+1][y2+1] + = c;

Every time the b The array does the above , Equivalent to ： Time complexity o(n2)

for(int i=x1;i<=x2;i++)
  for(int j=y1;j<=y2;j++)
       a[i][j]+=c;

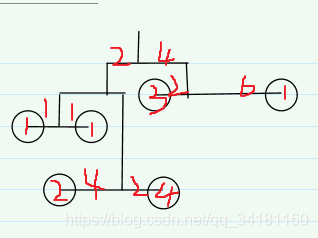
Let's draw a picture to understand the process ：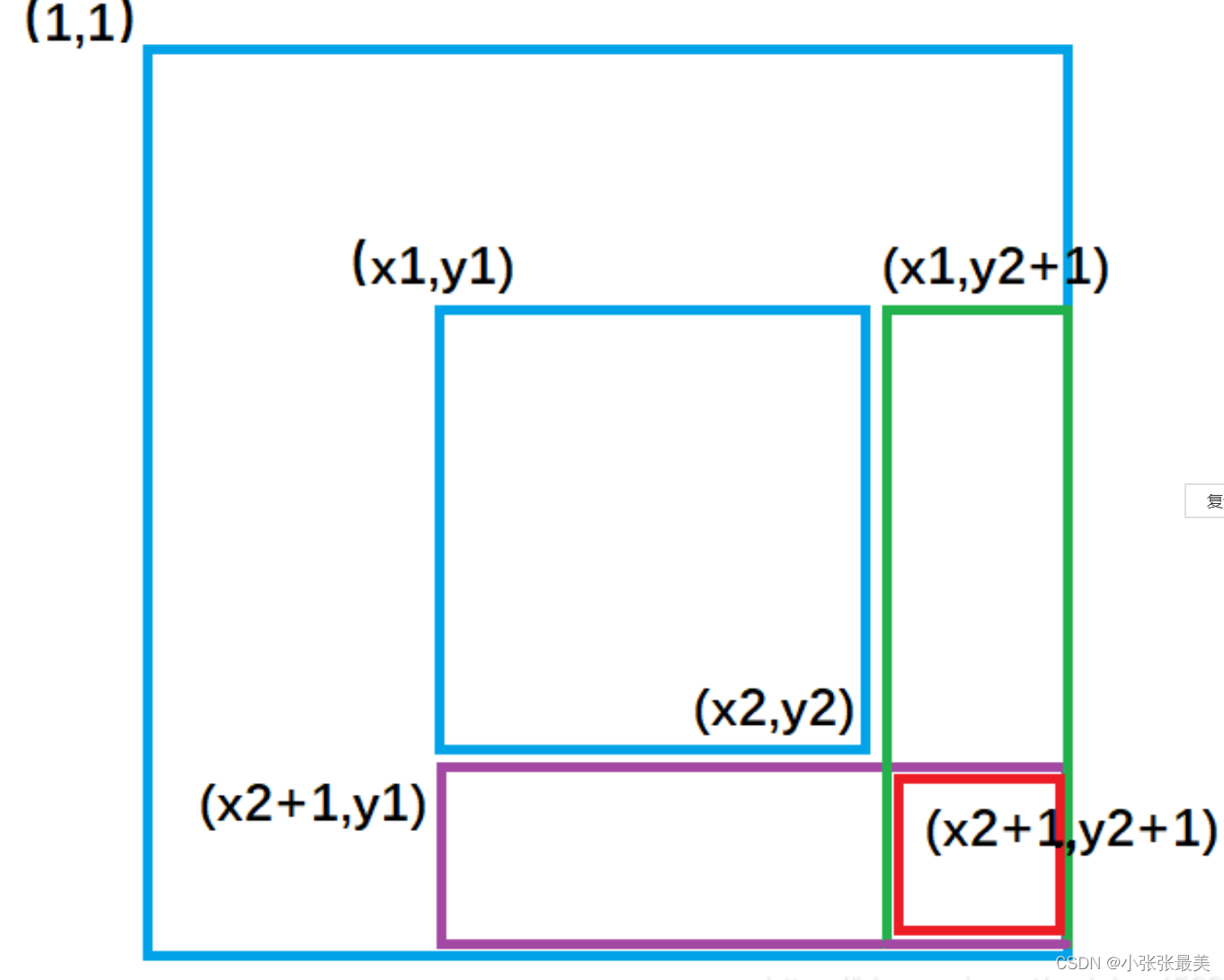

b[x1][ y1 ] +=c ; Corresponding graph 1 , Let the whole a The elements of the blue rectangular area in the array are added c.
b[x1,][y2+1]-=c ; Corresponding graph 2 , Let the whole a Subtract... From the elements of the green rectangular area in the array c, Keep its elements unchanged .
b[x2+1][y1]- =c ; Corresponding graph 3 , Let the whole a Subtract... From the area of the purple rectangle in the array c, Keep its elements unchanged .
b[x2+1][y2+1]+=c; Corresponding graph 4, Let the whole a The element of the red rectangular area in the array plus c, The in red is equivalent to being subtracted twice , One more time c, To restore it .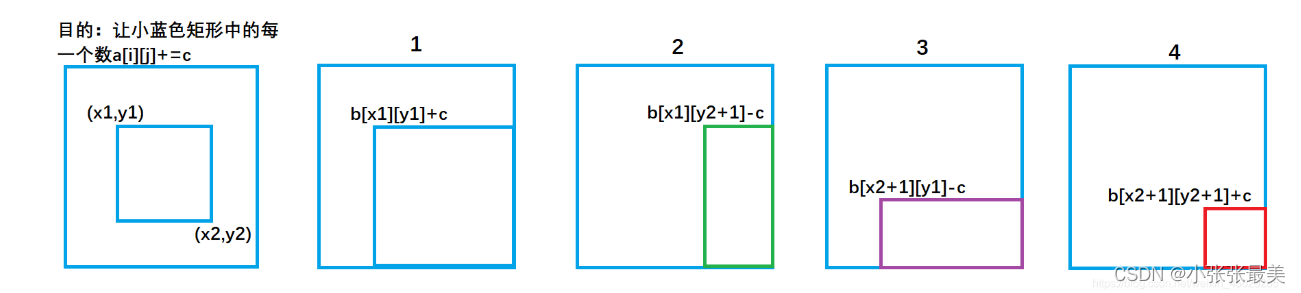

We encapsulate the above operations into an insert function :

void insert(int x1,int y1,int x2,int y2,int c)
{
         // Yes b The array performs an insert operation , It is equivalent to a Array (x1,y1) To (x2,y2) The elements between are added c
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}

We can imagine a Array is empty , that b The array is also empty at first , But actually a The array is not empty , So every time we let (i,j) From the upper left corner to (i,j) Is the element in the upper right corner area ( It's actually the area of a small square ) To insert c=a[i][j], Equivalent to the original array a in (i,j) To (i,j) Within the scope of Combined with the a[i][j] , So execute n*m Insert operations , We successfully built the differential b Array .

This is called saving the country by curve .

The code is as follows ：

  for(int i=1;i<=n;i++)
  {
    
      for(int j=1;j<=m;j++)
      {
    
          insert(i,j,i,j,a[i][j]);    // Build a differential array 
      }
  }

Two dimensional difference —— The template questions AcWing 798. Difference matrix
Give (x1, y1) It's the upper left corner ,(x2, y2) Add... To all elements of the submatrix in the lower right corner c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

Example
AcWing 798. Difference matrix
Enter a n That's ok m The integer matrix of columns , Input again q Operations , Each operation contains five integers x1,y1,x2,y2,c, among (x1,y1) and (x2,y2) Represents the upper left and lower right coordinates of a submatrix .
For each operation, add the value of each element in the selected sub matrix c.
Please output the matrix after all operations .

Input format
The first line contains integers n,m,q.

Next n That's ok , Each row contains m It's an integer , Represents an integer matrix .

Next q That's ok , Each row contains 5 It's an integer x1,y1,x2,y2,c, Represents an operation .

Output format
common n That's ok , Each row m It's an integer , Represents the final matrix after all operations are completed .

Data range
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤ The values of the elements in the matrix ≤1000
sample input ：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
sample output ：
2 3 4 1
4 3 4 1
2 2 2 2

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
    
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
int main()
{
    
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i++)
    {
    
        for (int j = 1; j <= m; j++)
        {
    
            insert(i, j, i, j, a[i][j]);      // Build a differential array 
        }
    }
    while (q--)
    {
    
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    for (int i = 1; i <= n; i++)
    {
    
        for (int j = 1; j <= m; j++)
        {
    
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  // Two dimensional prefixes and 
        }
    }
    for (int i = 1; i <= n; i++)
    {
    
        for (int j = 1; j <= m; j++)
        {
    
            printf("%d ", b[i][j]);
        }
        printf("\n");
    }
    return 0;
}

Three dimensional difference

Observe one dimension

b[l] = s[l] - s[l-1]  

+s[l] , -s[l-1]
A two-dimensional

b[i][j] = s[i][j] - s[i-1][j] - s[i][j-1] + s[i-1][j-1]

-s[i-1][j] , -s[i][j-1] , +s[i][j] , +s[i-1][j-1]
If there is an odd number minus one, it is negative , Even minus one is positive
0 0 { s[ i - 0 ][ j - 0 ] = s[ i ][ j ] } +1
0 1 { s[ i - 0 ][ j - 1 ] = s[ i ][ j - 1] } -1
1 0 { s[ i - 1 ][ j- 0 ] = s[ i - 1 ][ j ] } -1
1 1 { s[ i - 1][ j - 1 ]} -1
If will be located (x1, y1) and (x2, y2) Add c:

b[x1][y1] += c;  //00
b[x1][y2+1] -= c; //01
b[x2+1][y1] -= c; //10
b[x2+1][y2+1] += c; //11

In the same way
The three dimensional

b[i][j][k] = s[i][j][k] - s[i-1][j][k] - s[i][j-1][k] + s[i-1][j-1][k]- s[i][j][k-1] + s[i-1][j][k-1] + s[i][j-1][k-1] - s[i-1][j-1][k-1];

Will be located at (x1, y1, z1) and (x2, y2, z2) Add c:

b[x1    ][y1    ][z1    ]   += c;  // 000
b[x1    ][y1    ][z2 + 1]   -= c;  // 001
b[x1    ][y2 + 1][z1    ]   -= c;  // 010
b[x1    ][y2 + 1][z2 + 1]   += c;  // 011
b[x2 + 1][y1    ][z1    ]   -= c;  // 100
b[x2 + 1][y1    ][z2 + 1]   += c;  // 101
b[x2 + 1][y2 + 1][z1    ]   += c;  // 110
b[x2 + 1][y2 + 1][z2 + 1]   -= c;  // 111

Example
AcWing 1232. Three body attack
The triad will attack the earth .
To defend against attack , The earth people sent A×B×C warship , Line up in space A layer B That's ok C The cube of columns .
among , The first i Layer j Xing di k The ships of the line （ It's a warship (i,j,k)） The life value of is d(i,j,k).
The triad will launch a war against the earth m round “ Cube attack ”, Each attack deals the same damage to all warships in a cube .
In particular , The first t Round attack 7 Parameters lat,rat,lbt,rbt,lct,rct,ht describe ;
All satisfied i∈[lat,rat],j∈[lbt,rbt],k∈[lct,rct] The warships of (i,j,k) Will receive ht The damage of .
If a warship's total cumulative damage exceeds its defense , Then this warship will explode .
Earth Commander wants you to tell him , After which attack did the first warship explode .

Input format
The first line includes 4 A positive integer A,B,C,m;

The second line contains A×B×C It's an integer , Among them the first ((i−1)×B+(j−1))×C+(k−1)+1 The number is d(i, j, k);
The first 3 To the first m+2 In line , The first (t − 2) Line inclusion 7 A positive integer lat, rat, lbt, rbt, lct, rct, ht.

Output format
The warship that outputs the first explosion exploded after which round of attack .
There must be such a warship .

Data range
1≤A×B×C≤106,
1≤m≤106,
0≤d(i, j, k), ht≤109,
1≤lat≤rat≤A,
1≤lbt≤rbt≤B,
1≤lct≤rct≤C
layer 、 That's ok 、 The column numbers are from 1 Start .

sample input ：
2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2
sample output ：
2
Sample explanation
In the 2 After a round of attack , Warship (1,1,1) A total of 2 Point injury , Exceeding its defense will lead to an explosion .

Be careful A×B×C<=1e6, Opening a three-dimensional array may timeout , Convert the corresponding three-dimensional coordinates into one-dimensional coordinates (i×B+j)×k
Too many queries , Two point solution , Find No 1 A bombed warship
Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int const N=2e6+10;// One more side  (i,j,k,+1);
int a,b,c,m;
ll s[N];// Original array ;
ll bb[N],dp[N]; // Difference array ;
 int op[N/2][7];
int d[8][4]=
{
    
    {
    0,0,0,1},{
    0,0,1,-1},{
    0,1,0,-1},{
    0,1,1,1},
    {
    1,0,0,-1},{
    1,0,1,1},{
    1,1,0,1},{
    1,1,1,-1},
};
int get(int i,int j,int k)  // In the form of a one-dimensional array 
{
    
    return (i*b+j)*c+k;
}
bool check(int mid)// Judge whether it was the first one to be destroyed ;
{
    
    memcpy(bb,dp,sizeof bb);// Copy ;
    for(int i=1; i<=mid; i++)
    {
    
        // Will be located at (x1, y1, z1) and (x2, y2, z2) Between the original sequences are subtracted h:
        int x1 = op[i][0], x2 = op[i][1];
        int y1 = op[i][2], y2 = op[i][3];
        int z1 = op[i][4], z2 = op[i][5], h = op[i][6];
        bb[get(x1,     y1,     z1)]     -= h;
        bb[get(x1,     y1,     z2 + 1)] += h;
        bb[get(x1,     y2 + 1, z1)]     += h;
        bb[get(x1,     y2 + 1, z2 + 1)] -= h;
        bb[get(x2 + 1, y1,     z1)]     += h;
        bb[get(x2 + 1, y1,     z2 + 1)] -= h;
        bb[get(x2 + 1, y2 + 1, z1)]     -= h;
        bb[get(x2 + 1, y2 + 1, z2 + 1)] += h;
    }
    memset(s,0,sizeof s);  // The prefix sum is changed to the original array ;
    for(int i=1; i<=a; i++)
        for(int j=1; j<=b; j++)
            for(int k=1; k<=c; k++)
            {
    
                s[get(i,j,k)]=bb[get(i,j,k)];
                for(int u=1; u<8; u++)
                {
    
                    int x=i-d[u][0],y=j-d[u][1];
                    int z=k-d[u][2],t=d[u][3];
                    s[get(i,j,k)]-=s[get(x,y,z)]*t;
                }
                if(s[get(i,j,k)]<0)
                    return true;
            }
    return false;

}
int main()
{
    
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);

    cin>>a>>b>>c>>m;

    for(int i=1; i<=a; i++)
        for(int j=1; j<=b; j++)
            for(int k=1; k<=c; k++)
                cin>>s[get(i,j,k)];

    // Difference 
    for(int i=1; i<=a; i++)
        for(int j=1; j<=b; j++)
            for(int k=1; k<=c; k++)
                for(int u=0; u<8; u++) // altogether 8 In this case ;000 001 010...
                {
    
                    int x=i-d[u][0],y=j-d[u][1],z=k-d[u][2],t=d[u][3];
                    dp[get(i,j,k)]+=s[get(x,y,z)]*t;
                }

    // Input m Operations ;
    for(int i=1; i<=m; i++)
        for(int j=0; j<7; j++)
            cin>>op[i][j];

    // Two points search 
    int l=1,r=m;
    while(l<r)
    {
    
        int mid=l+r >> 1;
        if(check(mid)) // If the first mid The operation has blown up , Look forward to 
            r=mid;
        else
            l=mid+1;
    }

    cout<<r<<endl;

    return 0;
}