Record of force deduction and question brushing

Dynamic programming

The first example Problem analysis and problem solving ideas of the longest palindrome substring

---

---

Preface

Tips ： Here you can add the general content to be recorded in this article ：
I am a novice , Blogging is pure self memory , Convenient to review , No joy, no spray.

---

Tips ： The following is the main body of this article , The following cases can be used for reference

One 、 What is dynamic planning ？

It's straight from the bottom , The most simple , The smallest problem f(1) and f(2) Start pushing up , Until we get the answer we want f(20), This is the idea of dynamic planning , That's why dynamic programming is generally free of recursion , It 's the loop iteration that does the calculation .

Two 、 The steps to solve the problem

1. Problem description

Give you a string s, find s The longest palindrome substring in .
1 <= s.length <= 1000
s It consists only of numbers and English letters
Be careful ： The substring is continuous

Input ：s = “babad”
Output ：“bab”
explain ：“aba” It's the same answer .

Input ：s = “cbbd”
Output ：“bb”

2. Problem analysis

The problem of finding the longest palindrome substring can be transformed into ： When from the first i Character to character j individual The substring composed of characters is the longest palindrome substring , solve i and j

3. Problem solving steps

1. State definition ：

Definition dp[ i ][ j ] Express s Of the i Character to character j A substring of characters , Whether it can form a palindrome substring
true Represents the interval [i,j] Palindrome string
false Represents the interval [i,j] Not a palindrome string

2. State transition equation ：

dp[ i ][ j ] Can it form a palindrome substring , It depends on two factors

• The current first element is the same ,s[i] == s[j]
• The preceding substring is palindrome ,dp[i+1][j-1] == true

3. The state transition equation supplements the special case

The second use case above ,s = “cbbd”, When left = 1,right = 2 when , The judgment is ：

s[1] == s[2] -> true
dp[2][1] -> false
Which leads to d[1][2] Wrong set as false
The root of the mistake is , When 「 The leading and trailing elements are next to 」 When left + 1 and right - 1 The problems caused

therefore , according to 「 Whether the leading and trailing elements are next to 」 Rearrange the state transition equation

• When the leading and trailing elements are next to ,right - left == 1
  If the first and last elements are the same , Can form palindrome string
  If the first and last elements are different , Does not form a palindrome string
• When there is a gap between the first and last elements ,right - left > 1
  The current leading and trailing elements are the same s[i] == s[j], And the preceding substring is palindrome dp[i+1][j-1] == true, Can form palindrome string

4. Problem solving steps

1. Initialize 2D array

example ：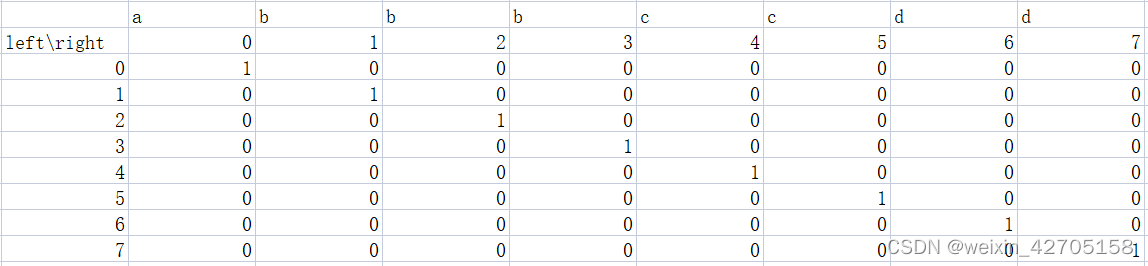

2. The code is as follows （ Example ）

class Solution {
    
public:
    string longestPalindrome(string s) {
    
       int n=s.size();
       vector<vector<bool>>dp(n,vector<bool>(n,false));
       for(int i=0;i<n;i++)
       {
    
           dp[i][i]=true;
       }
       int begin=0;
       int maxlength=1;
       for(int left=n-1;left>=0;left--)
       {
    
           for(int right=left+1;right<n;right++)
           {
    
               if(right-left==1)
               {
    
                   if(s[left]==s[right])
                   {
    
                       dp[left][right]=true;
                   }
                   else{
    
                       dp[left][right]=false;
                   }
               }
               else{
    
                   if(s[left]==s[right]&&dp[left+1][right-1]==true)
                   {
    
                       dp[left][right]=true;
                   }
                   else{
    
                       dp[left][right]=false;
                   }
               }
               if(dp[left][right]==true&&right-left+1>maxlength)
               {
    
                   begin=left;
                   maxlength=right-left+1;
               }
           }
       }
       return s.substr(begin,maxlength);
    }
};

3. Thought analysis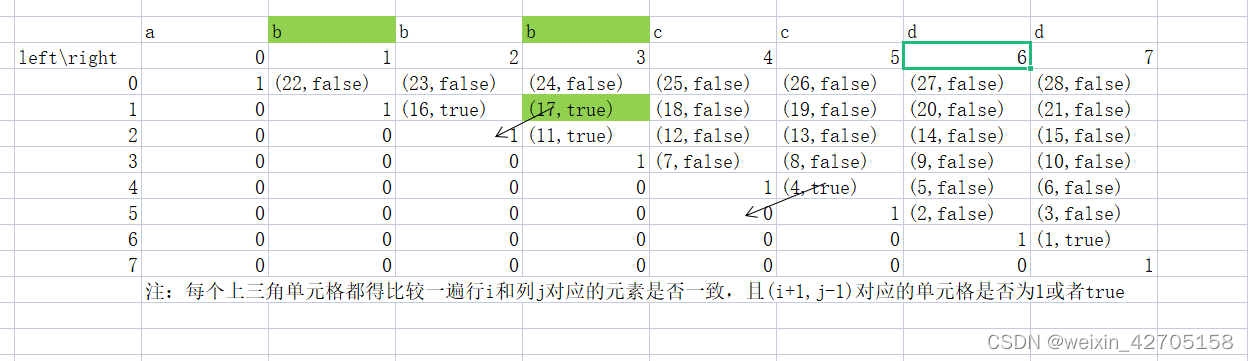

---

Here is the reference

Quote the original ：

`
https://leetcode-cn.com/problems/longest-palindromic-substring/solution/by-dodo_1202-k031/
、