当前位置:网站首页>差分(一维,二维,三维) 蓝桥杯三体攻击
差分(一维,二维,三维) 蓝桥杯三体攻击
2022-07-06 09:25:00 【是小张张呀 zsy】
如果一维二维已经没问题的可直接跳转
一维差分
首先给定一个原数组a:a[1], a[2], a[3], a[n];
然后我们构造一个数组b : b[1] ,b[2] , b[3], b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +, + b[i]
a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。
考虑构造差分b数组
最为直接的方法
如下:
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] =a [3] - a[2];
…
b[n] = a[n] - a[n-1];
有b数组,通过前缀和运算,就可以在O(n) 的时间内得到a数组 。
一维差分 —— 模板题 AcWing 797. 差分
给区间[l, r]中的每个数加上c:b[l] += c, b[r + 1] -= c
例题
AcWing797. 差分
输入一个长度为 n 的整数序列。接下来输入 m 个操作,每个操作包含三个整数 l,r,c,表示将序列中 [l,r] 之间的每个数加上 c。
请你输出进行完所有操作后的序列。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数序列。
接下来 m 行,每行包含三个整数 l,r,c,表示一个操作。
输出格式
共一行,包含 n 个整数,表示最终序列。
数据范围
1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000
输入样例:
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例:
3 4 5 3 4 2
#include<bits/stdc+.和>
using namespace std;
const int N=1e5+10;
int a[N],b[N];
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
b[i]=a[i]-a[i-1]; //构建差分数组
}
int l,r,c;
while(m--)
{
scanf("%d%d%d",&l,&r,&c);
b[l]+=c; //将序列中[l, r]之间的每个数都加上c
b[r+1]-=c;
}
for(int i=1;i<=n;i++)
{
a[i]=b[i]+a[i-1]; //前缀和运算
printf("%d ",a[i]);
}
return 0;
}
二维差分
作者:z林深时见鹿
如果扩展到二维,我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的,考虑二维差分。
a[][]数组是b[][]数组的前缀和数组,那么b[][]是a[][]的差分数组
原数组: a[i][j]
我们去构造差分数组: b[i][j]
使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。
如何构造b数组呢?
我们去逆向思考。
同一维差分,我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作,可以由O(n*n)的时间复杂度优化成O(1)
已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角,以(x2,y2)为右下角所围成的矩形区域;
始终要记得,a数组是b数组的前缀和数组,比如对b数组的b[i][j]的修改,会影响到a数组中从a[i][j]及往后的每一个数。
假定我们已经构造好了b数组,类比一维差分,我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c 时间复杂度o(1)
b[x1][y1] + = c;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
每次对b数组执行以上操作,等价于: 时间复杂度o(n2)
for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
a[i][j]+=c;
我们画个图去理解一下这个过程: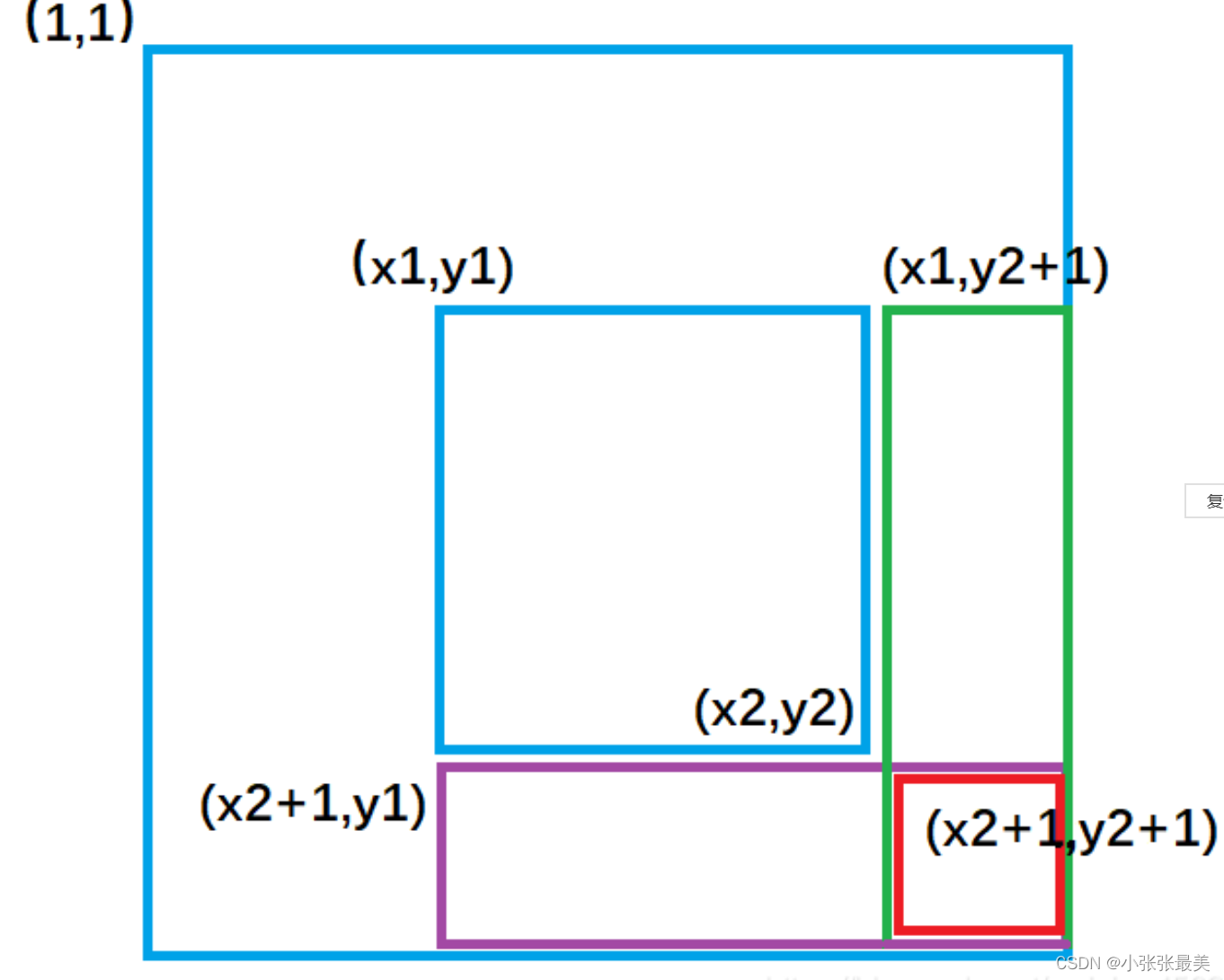
b[x1][ y1 ] +=c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2+1]-=c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y1]- =c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y2+1]+=c; 对应图4,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。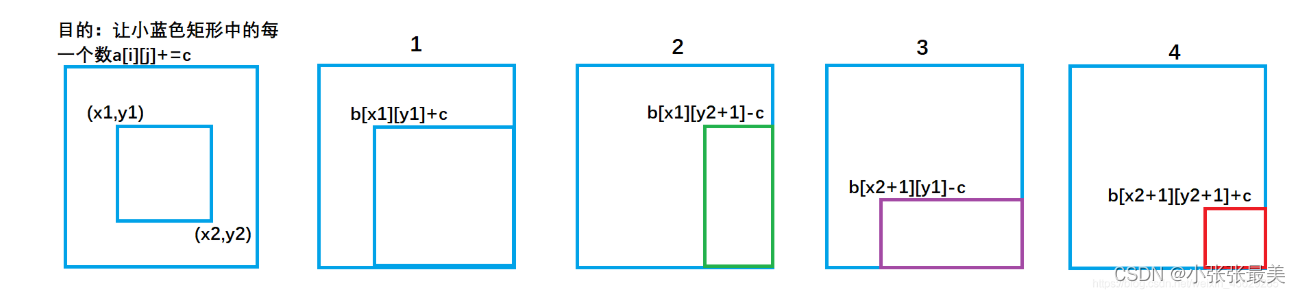
我们将上述操作封装成一个插入函数:
void insert(int x1,int y1,int x2,int y2,int c)
{
//对b数组执行插入操作,等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
我们可以先假想a数组为空,那么b数组一开始也为空,但是实际上a数组并不为空,因此我们每次让以(i,j)为左上角到以(i,j)为右上角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j],等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n*m次插入操作,就成功构建了差分b数组.
这叫做曲线救国。
代码如下:
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
insert(i,j,i,j,a[i][j]); //构建差分数组
}
}
二维差分 —— 模板题 AcWing 798. 差分矩阵
给以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵中的所有元素加上c:
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c
例题
AcWing 798. 差分矩阵
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 n,m,q。
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1≤n,m≤1000,
1≤q≤100000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤c≤1000,
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> a[i][j];
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
insert(i, j, i, j, a[i][j]); //构建差分数组
}
}
while (q--)
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
printf("%d ", b[i][j]);
}
printf("\n");
}
return 0;
}
三维差分
观察一维
b[l] = s[l] - s[l-1]
+s[l] , -s[l-1]
二维
b[i][j] = s[i][j] - s[i-1][j] - s[i][j-1] + s[i-1][j-1]
-s[i-1][j] , -s[i][j-1] , +s[i][j] , +s[i-1][j-1]
有奇数个减一是负,偶数个减一是正
0 0 { s[ i - 0 ][ j - 0 ] = s[ i ][ j ] } +1
0 1 { s[ i - 0 ][ j - 1 ] = s[ i ][ j - 1] } -1
1 0 { s[ i - 1 ][ j- 0 ] = s[ i - 1 ][ j ] } -1
1 1 { s[ i - 1][ j - 1 ]} -1
若将位于(x1, y1)和(x2, y2)之间的原序列都加上c:
b[x1][y1] += c; //00
b[x1][y2+1] -= c; //01
b[x2+1][y1] -= c; //10
b[x2+1][y2+1] += c; //11
同理得到
三维
b[i][j][k] = s[i][j][k] - s[i-1][j][k] - s[i][j-1][k] + s[i-1][j-1][k]- s[i][j][k-1] + s[i-1][j][k-1] + s[i][j-1][k-1] - s[i-1][j-1][k-1];
将位于(x1, y1, z1)和(x2, y2, z2)之间的原序列都加上c:
b[x1 ][y1 ][z1 ] += c; // 000
b[x1 ][y1 ][z2 + 1] -= c; // 001
b[x1 ][y2 + 1][z1 ] -= c; // 010
b[x1 ][y2 + 1][z2 + 1] += c; // 011
b[x2 + 1][y1 ][z1 ] -= c; // 100
b[x2 + 1][y1 ][z2 + 1] += c; // 101
b[x2 + 1][y2 + 1][z1 ] += c; // 110
b[x2 + 1][y2 + 1][z2 + 1] -= c; // 111
例题
AcWing 1232. 三体攻击
三体人将对地球发起攻击。
为了抵御攻击,地球人派出了 A×B×C 艘战舰,在太空中排成一个 A 层 B 行 C 列的立方体。
其中,第 i 层第 j 行第 k 列的战舰(记为战舰 (i,j,k))的生命值为 d(i,j,k)。
三体人将会对地球发起 m 轮“立方体攻击”,每次攻击会对一个小立方体中的所有战舰都造成相同的伤害。
具体地,第 t 轮攻击用 7 个参数 lat,rat,lbt,rbt,lct,rct,ht 描述;
所有满足 i∈[lat,rat],j∈[lbt,rbt],k∈[lct,rct] 的战舰 (i,j,k) 会受到 ht 的伤害。
如果一个战舰累计受到的总伤害超过其防御力,那么这个战舰会爆炸。
地球指挥官希望你能告诉他,第一艘爆炸的战舰是在哪一轮攻击后爆炸的。
输入格式
第一行包括 4 个正整数 A,B,C,m;
第二行包含 A×B×C 个整数,其中第 ((i−1)×B+(j−1))×C+(k−1)+1 个数为 d(i, j, k);
第 3 到第 m+2 行中,第 (t − 2) 行包含 7 个正整数 lat, rat, lbt, rbt, lct, rct, ht。
输出格式
输出第一个爆炸的战舰是在哪一轮攻击后爆炸的。
保证一定存在这样的战舰。
数据范围
1≤A×B×C≤106,
1≤m≤106,
0≤d(i, j, k), ht≤109,
1≤lat≤rat≤A,
1≤lbt≤rbt≤B,
1≤lct≤rct≤C
层、行、列的编号都从 1 开始。
输入样例:
2 2 2 3
1 1 1 1 1 1 1 1
1 2 1 2 1 1 1
1 1 1 2 1 2 1
1 1 1 1 1 1 2
输出样例:
2
样例解释
在第 2 轮攻击后,战舰 (1,1,1) 总共受到了 2 点伤害,超出其防御力导致爆炸。
注意A×B×C<=1e6,开三维数组可能会超时,把对应三维坐标转化成一维坐标(i×B+j)×k
查询次数过多,二分解决,找到第1个被炸毁的战舰
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int const N=2e6+10;//多出一个面 (i,j,k,+1);
int a,b,c,m;
ll s[N];//原数组;
ll bb[N],dp[N]; //差分数组;
int op[N/2][7];
int d[8][4]=
{
{
0,0,0,1},{
0,0,1,-1},{
0,1,0,-1},{
0,1,1,1},
{
1,0,0,-1},{
1,0,1,1},{
1,1,0,1},{
1,1,1,-1},
};
int get(int i,int j,int k) //以一维数组的形式
{
return (i*b+j)*c+k;
}
bool check(int mid)//判断是否是第一个被炸毁的;
{
memcpy(bb,dp,sizeof bb);//拷贝;
for(int i=1; i<=mid; i++)
{
//将位于(x1, y1, z1)和(x2, y2, z2)之间的原序列都减去h:
int x1 = op[i][0], x2 = op[i][1];
int y1 = op[i][2], y2 = op[i][3];
int z1 = op[i][4], z2 = op[i][5], h = op[i][6];
bb[get(x1, y1, z1)] -= h;
bb[get(x1, y1, z2 + 1)] += h;
bb[get(x1, y2 + 1, z1)] += h;
bb[get(x1, y2 + 1, z2 + 1)] -= h;
bb[get(x2 + 1, y1, z1)] += h;
bb[get(x2 + 1, y1, z2 + 1)] -= h;
bb[get(x2 + 1, y2 + 1, z1)] -= h;
bb[get(x2 + 1, y2 + 1, z2 + 1)] += h;
}
memset(s,0,sizeof s); //前缀和求更改后原数组;
for(int i=1; i<=a; i++)
for(int j=1; j<=b; j++)
for(int k=1; k<=c; k++)
{
s[get(i,j,k)]=bb[get(i,j,k)];
for(int u=1; u<8; u++)
{
int x=i-d[u][0],y=j-d[u][1];
int z=k-d[u][2],t=d[u][3];
s[get(i,j,k)]-=s[get(x,y,z)]*t;
}
if(s[get(i,j,k)]<0)
return true;
}
return false;
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
cin>>a>>b>>c>>m;
for(int i=1; i<=a; i++)
for(int j=1; j<=b; j++)
for(int k=1; k<=c; k++)
cin>>s[get(i,j,k)];
//差分
for(int i=1; i<=a; i++)
for(int j=1; j<=b; j++)
for(int k=1; k<=c; k++)
for(int u=0; u<8; u++) //一共8种情况;000 001 010...
{
int x=i-d[u][0],y=j-d[u][1],z=k-d[u][2],t=d[u][3];
dp[get(i,j,k)]+=s[get(x,y,z)]*t;
}
//输入m个操作;
for(int i=1; i<=m; i++)
for(int j=0; j<7; j++)
cin>>op[i][j];
//二分查找
int l=1,r=m;
while(l<r)
{
int mid=l+r >> 1;
if(check(mid)) //如果第mid操作有炸毁,往前找
r=mid;
else
l=mid+1;
}
cout<<r<<endl;
return 0;
}
边栏推荐
猜你喜欢

STM32如何使用STLINK下载程序:点亮LED跑马灯(库版本)
UCORE lab5 user process management experiment report
JS --- BOM details of JS (V)
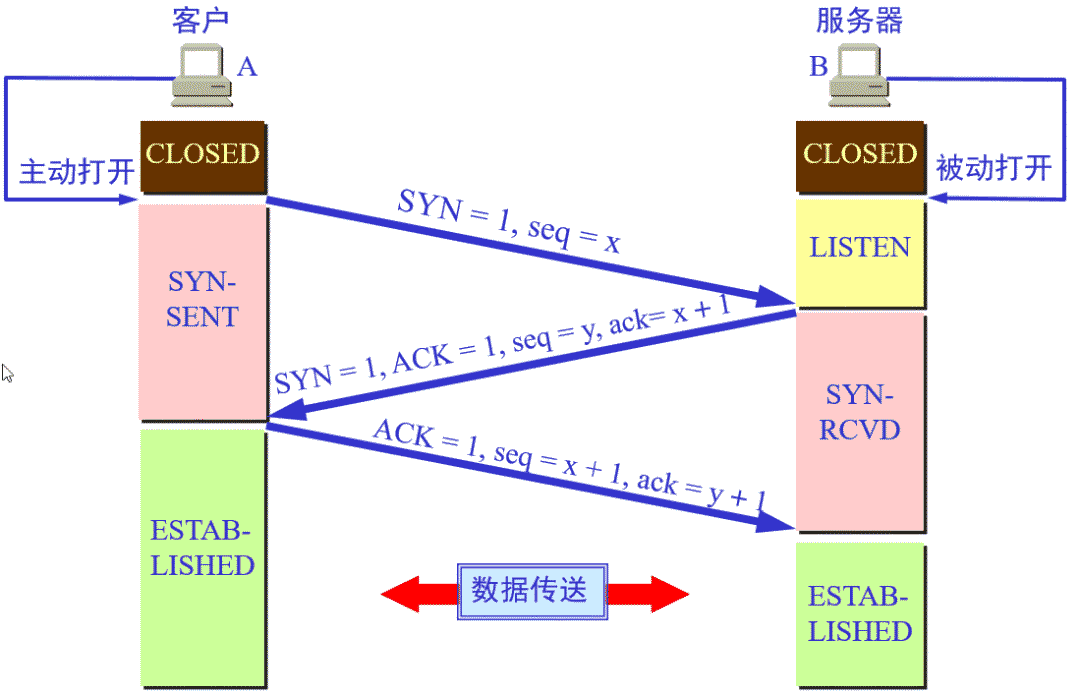
TCP的三次握手与四次挥手

How to become a good software tester? A secret that most people don't know
Eslint--- error: newline required at end of file but not found (EOL last) solution

Winter vacation daily question - maximum number of balloons
ucore lab7
What are the software testing methods? Show you something different

动态规划前路径问题优化方式
随机推荐
MySQL transactions
Es6---es6 content details
Cost accounting [16]
Cost accounting [14]
JS --- all basic knowledge of JS (I)
JS --- JS function and scope (II)
Lab 8 文件系统
JS --- detailed explanation of JS facing objects (VI)
动态规划前路径问题
The most detailed postman interface test tutorial in the whole network. An article meets your needs
Flex --- detailed explanation of flex layout attributes
ucorelab3
ucore lab5
学习记录:使用STM32外部输入中断
ucore lab 6
数据在内存中的存储&载入内存,让程序运行起来
ucore lab5
JS --- all knowledge of JS objects and built-in objects (III)
Mysql database (III) advanced data query statement
编程到底难在哪里?
