当前位置:网站首页>Introduction to deep learning linear algebra (pytorch)
Introduction to deep learning linear algebra (pytorch)
2022-07-03 10:33:00 【-Plain heart to warm】
Teacher Li Mu's study notes
linear algebra
linear algebra

Scalar
Simple operation
c = a + b
c = a·b
c = sin a
length
∣ a ∣ = { a i f a > 0 − a o t h e r w i s e |a| = \begin{cases} a& ifa > 0 \\ -a& otherwise \end{cases} ∣a∣={ a−aifa>0otherwise
∣ a + b ∣ ≤ ∣ a ∣ + ∣ b ∣ |a+b|\le|a| + |b| ∣a+b∣≤∣a∣+∣b∣
∣ a ⋅ b ∣ = ∣ a ∣ ⋅ ∣ b ∣ |a·b|=|a|·|b| ∣a⋅b∣=∣a∣⋅∣b∣
vector
Simple operation
c = a + b w h e r e c i = a i + b i c=a+b\ \ \ where\ c_i=a_i+b_i c=a+b where ci=ai+bi
c = α ⋅ b w h e r e c i = α b i c=\alpha·b\ \ \ where\ c_i=\alpha b_i c=α⋅b where ci=αbi
c = s i n a w h e r e c i = s i n a i c=sina\ \ \ where\ c_i=sina_i c=sina where ci=sinai
length
The length of the vector , That is, sum the squares of each element of the vector and then open the root
∣ ∣ a ∣ ∣ 2 = [ ∑ i = 1 m a i 2 ] 1 2 ||a||_2=[\sum_{i=1}^ma_i^2]^{1 \over 2} ∣∣a∣∣2=[∑i=1mai2]21
∣ ∣ a ∣ ∣ ≥ 0 f o r a l l a ||a|| \ge 0\ for\ all\ a ∣∣a∣∣≥0 for all a
Trigonometric Theorem ∣ ∣ a + b ∣ ∣ ≤ ∣ ∣ a ∣ ∣ + ∣ ∣ b ∣ ∣ ||a+b|| \le ||a|| + ||b|| ∣∣a+b∣∣≤∣∣a∣∣+∣∣b∣∣
If a Is a constant ∣ ∣ a ⋅ b ∣ ∣ = ∣ a ∣ ⋅ ∣ ∣ b ∣ ∣ ||a·b|| = |a|·||b|| ∣∣a⋅b∣∣=∣a∣⋅∣∣b∣∣
Green is c
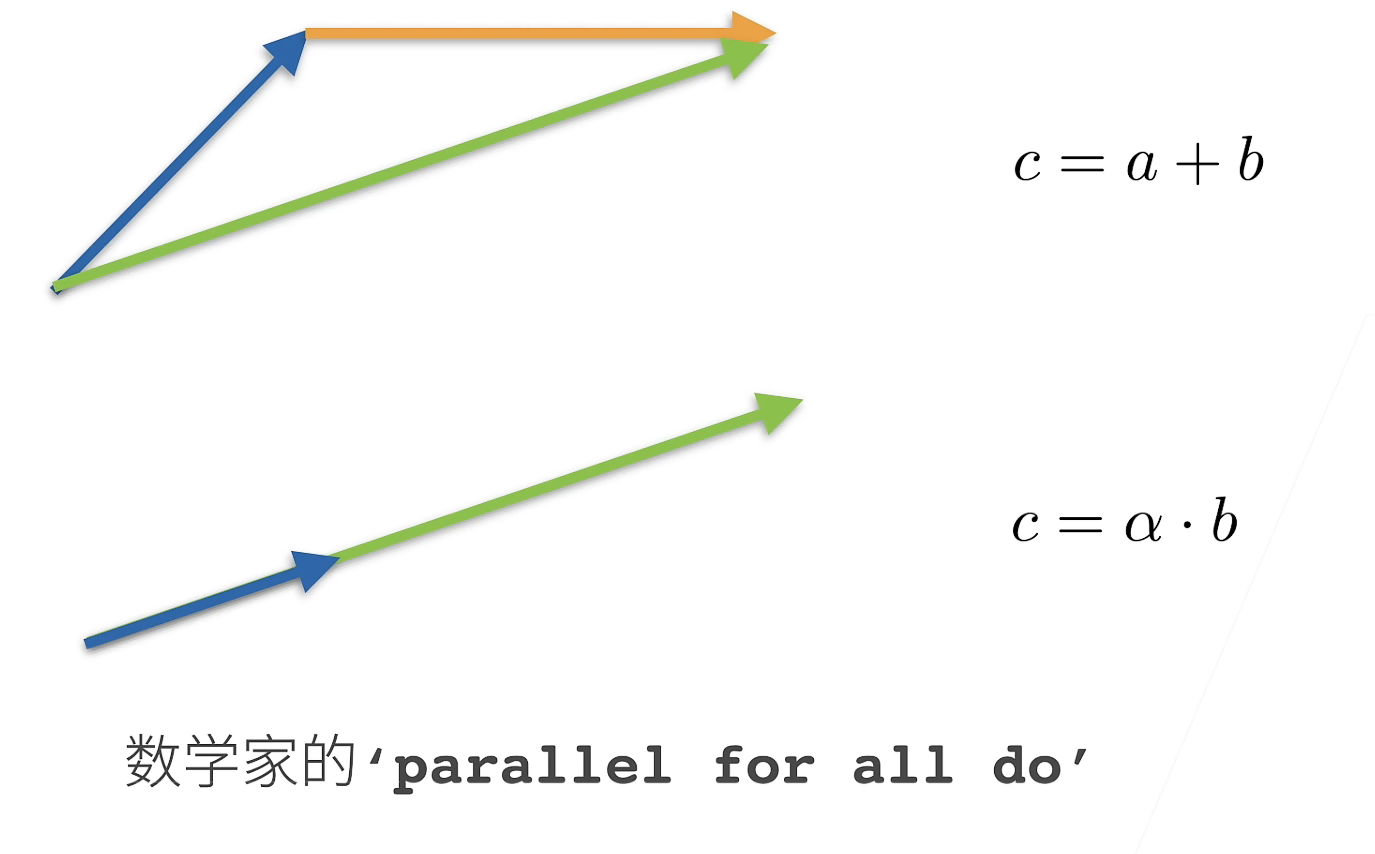
Point multiplication
a T b = ∑ i a i b i a^Tb=\sum_ia_ib_i aTb=∑iaibi
orthogonal
a T b = ∑ i a i b i = 0 a^Tb=\sum_ia_ib_i=0 aTb=∑iaibi=0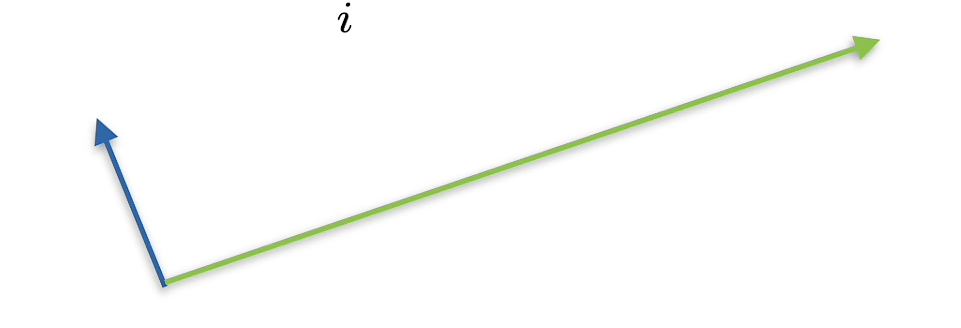
matrix
Simple operation

Multiplication ( Matrix times vector )

Multiplication ( Matrix times matrix )
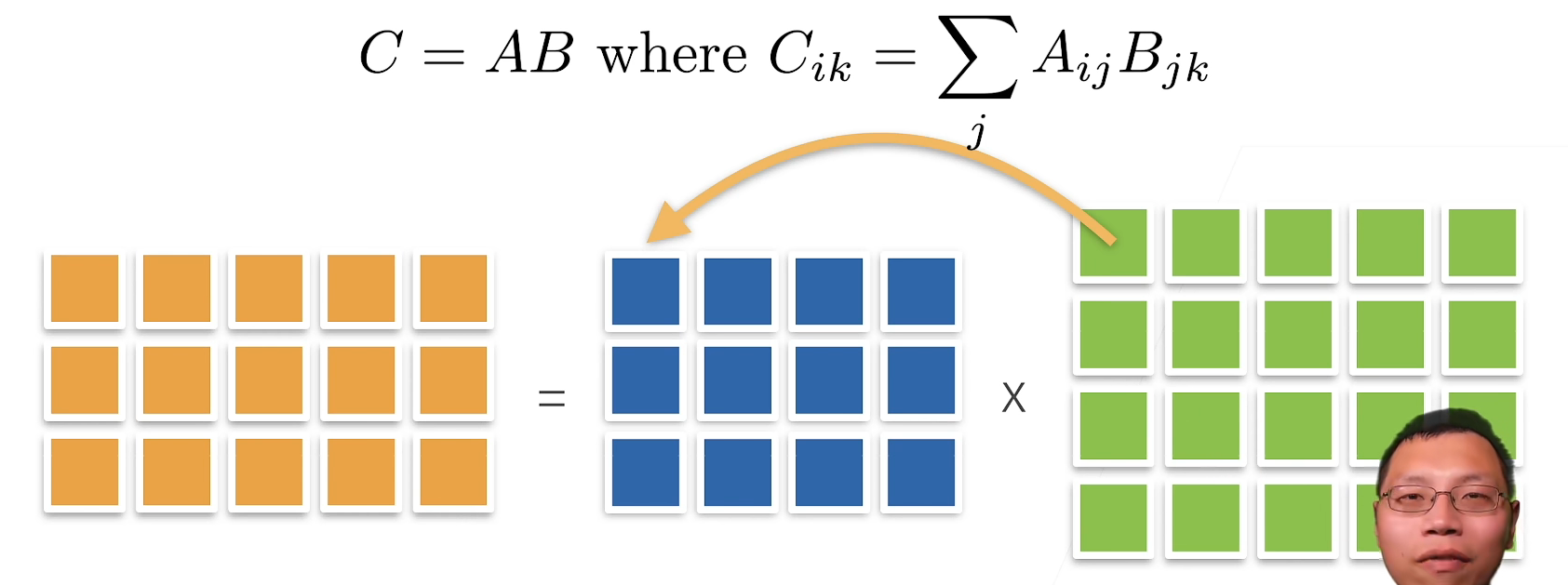
norm
c = A ⋅ b h e n c e ∣ ∣ c ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ⋅ ∣ ∣ b ∣ ∣ c=A·b\ hence\ ||c||\le||A||·||b|| c=A⋅b hence ∣∣c∣∣≤∣∣A∣∣⋅∣∣b∣∣
- Depends on how you measure b and c The length of
- Common norm
- Matrix constant : The minimum value that satisfies the above formula
- Frobenius norm
∣ ∣ A ∣ ∣ F r o b = [ ∑ i j A i j 2 ] 1 2 ||A||_{Frob}=[\sum_{ij}A^2_{ij}]^{1 \over 2} ∣∣A∣∣Frob=[ij∑Aij2]21
Special matrix
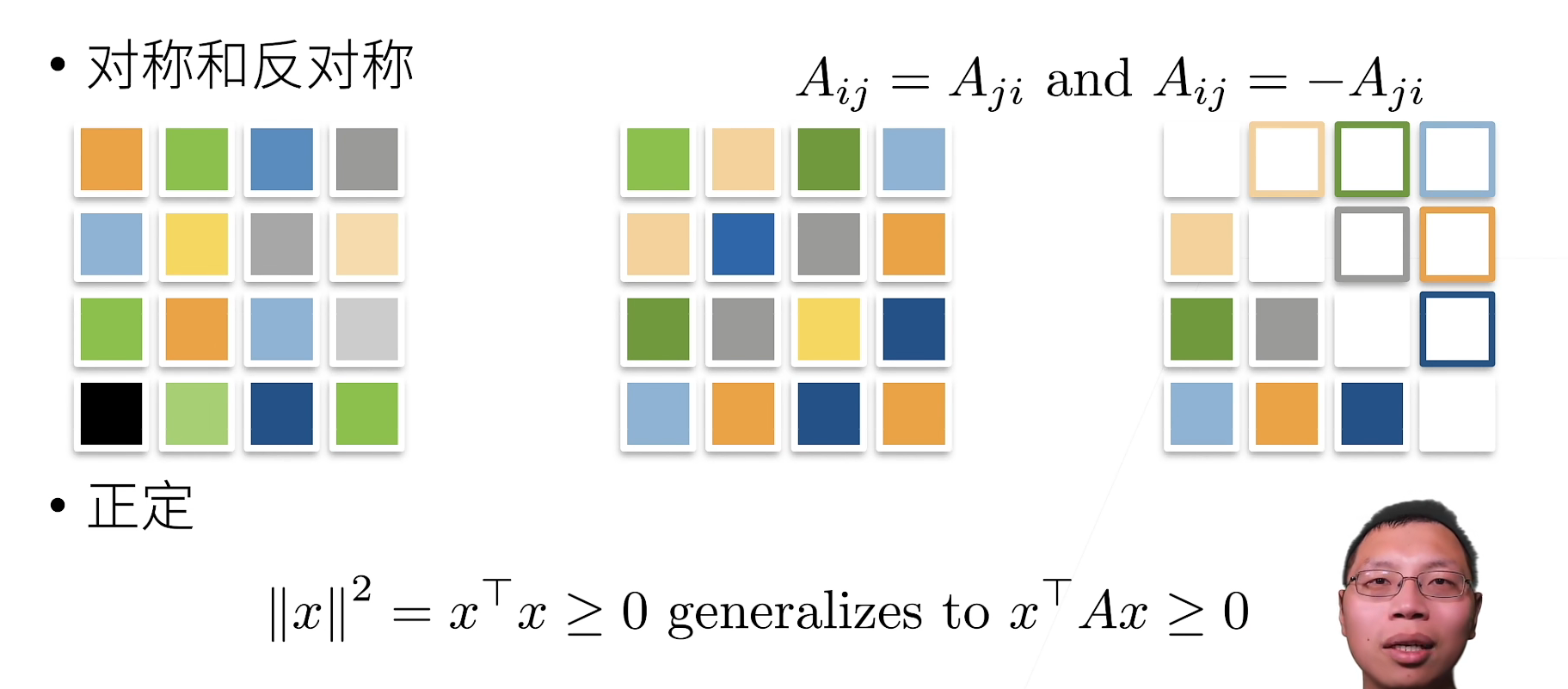
Orthogonal matrix
All rows are orthogonal to each other
All lines have a unit length \qquad U w i t h ∑ j U i j U k j = δ i k U\ with \sum_jU_{ij}U_{kj}=\delta_{ik} U with∑jUijUkj=δik
It can be written. U U T = 1 UU^T=1 UUT=1Permutation matrix
P w h e r e P i j = 1 i f a n d o n l y i f j = π ( i ) P\ where\ P_{ij}=1\ if\ and \ only\ if\ j=π(i) P where Pij=1 if and only if j=π(i)
A permutation matrix is an orthogonal matrix
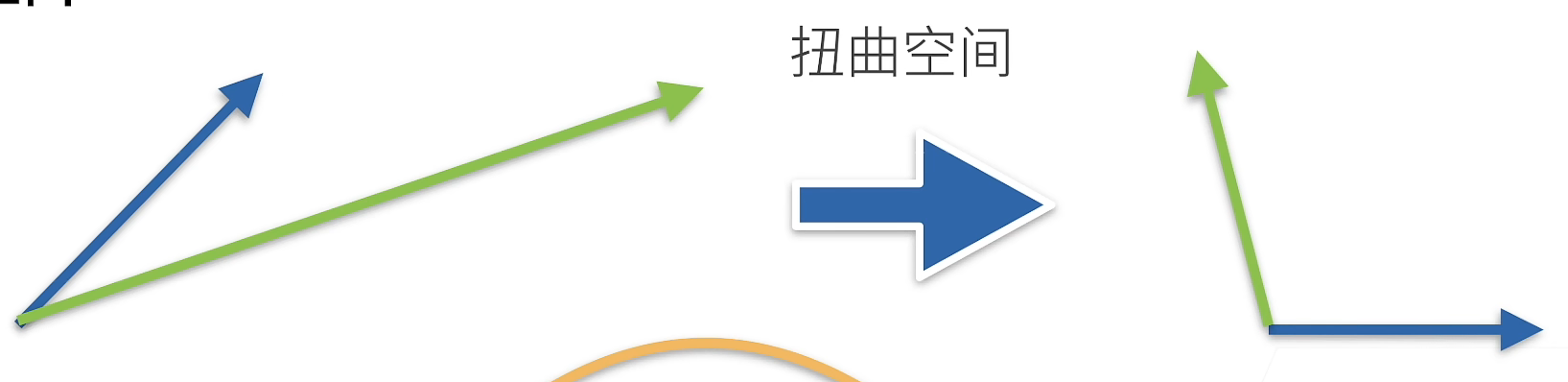
Eigenvectors and eigenvalues
Matrix is to distort space
- A vector that is not redirected by a matrix

- Symmetric matrices always find eigenvectors
Linear algebraic implementation
Scalar
Scalars are represented by tensors with only one element
import torch
x = torch.tensor([3.0])
y = torch.tensor([2.0])
x + y, x * y, x / y, x ** y
(tensor([5.]), tensor([6.]), tensor([1.5000]), tensor([9.]))
vector
You can think of vectors as a list of scalars
x = torch.arange(4)
x
tensor([0, 1, 2, 3])
Any element is accessed through the index of the tensor
x[3]
tensor(3)
index from 0 At the beginning , Mathematical index It's from 1 At the beginning
The length of the access tensor
len(x)
4
Tensor with only one axis , Character has only one element
x.shape
torch.size([4])
matrix
By specifying two components m and n To create a character named m × n Matrix
A = torch.arange(20).reshape(5, 4)
A
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
The transpose of the matrix
A.T
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
Symmetric matrix (symmetric matrix)A Equal to its transpose : A = A T A=A^T A=AT
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
tensor([[1, 2, 3],
[2, 0, 4],
[3, 4, 5]])
B == B.T
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
Just like a vector is a generalization of scalar , A matrix is a generalization of a vector , We can build data structures with more axes
X = torch.arange(24).reshape(2, 3, 4)
X
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
Given any two tensors with the same properties , Any structure settled by element duality will be a tensor of the same character .
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # By allocating new memory , take A A copy of is assigned to B
A, A+B
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]]),
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]]))
The multiplication of two matrices by elements is called Hadamaji (Hadamard product)( Mathematical symbols ⊙)
A * B
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]])
a = 2
X =torch.arange(24).reshape(2, 3, 4)
a+X, (a*X).shape
(tensor([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]]),
torch.Size([2, 3, 4]))
Calculate the sum of its elements
x = torch.arange(4, dtype=torch.float32)
x, x.sum()
(tensor([0., 1., 2., 3.]), tensor(6.))
Specifies the axis of the summation tensor
A = torch.arange(20*2).reshape(2, 5, 4)
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
(tensor([[20, 22, 24, 26],
[28, 30, 32, 34],
[36, 38, 40, 42],
[44, 46, 48, 50],
[52, 54, 56, 58]]),
torch.Size([5, 4]))
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
(tensor([[ 40, 45, 50, 55],
[140, 145, 150, 155]]),
torch.Size([2, 4]))
A.sum(axis=[0, 1, 2]) # Same as `A.sum()`
tensor(780)
It can be understood as axis=? , Just get rid of that dimension
A quantity related to summation is Average (mean or average)
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A.mean(), A.sum() / A.numel()
(tensor(9.5000), tensor(9.5000))
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
(tensor([ 8., 9., 10., 11.]), tensor([ 8., 9., 10., 11.]))
Keep the number of axes unchanged when calculating the sum or mean
sum_A = A.sum(axis=1, keepdims=True)
sum_A
tensor([[ 6.],
[22.],
[38.],
[54.],
[70.]])

Broadcast A Divide sum_A
A / sum_A
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
[0.1818, 0.2273, 0.2727, 0.3182],
[0.2105, 0.2368, 0.2632, 0.2895],
[0.2222, 0.2407, 0.2593, 0.2778],
[0.2286, 0.2429, 0.2571, 0.2714]])
Calculation of an axis A Cumulative sum of elements
A.cumsum(axis=0)
tensor([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]])
Dot product is the sum of the product of elements in the same position
y = torch.ones(4, dtype=torch.float32)
x, y, torch.dot(x, y)
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
We can perform multiplication by element , Then sum to represent the dot product of the two vectors
torch.sum(x * y)
tensor(6.)
Matrix vector product Ax Is a length of m The column vector , Its i t h i^{th} ith Elements are dot products a i T x a_i^Tx aiTx
print(A)
print(x)
A.shape, x.shape, torch.mv(A, x)
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([0., 1., 2., 3.])
(torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.]))
We can put the matrix - Matrix multiplication AB Think of it as simply performing m Submatrix - Vector product , And spliced the results together , formation n X m matrix
B = torch.ones(4, 3)
torch.mm(A, B)
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])
L 2 L_2 L2 norm Is the square root of the sum of squares of vector elements :
∣ ∣ x ∣ ∣ 2 = ∑ i = 1 n x i 2 ||x||_2= \sqrt{\sum_{i=1}^nx_i^2} ∣∣x∣∣2=i=1∑nxi2
u = torch.tensor([3.0, -4.0])
torch.norm(u)
tensor(5.)
norm Is the length of a vector or matrix
L 1 L_1 L1 norm , It is expressed as the sum of the absolute values of the vector elements :
∣ ∣ x ∣ ∣ 1 = ∑ i = 1 n ∣ x i ∣ ||x||_1=\sum_{i=1}^n|x_i| ∣∣x∣∣1=i=1∑n∣xi∣
torch.abs(u).sum()
tensor(7.)
Matrix Frobenius norm (Frobenius norm) Is the square root of the sum of squares of matrix elements :
∣ ∣ X ∣ ∣ F = ∑ i = 1 m ∑ j = 1 n x i j 2 ||X||_F=\sqrt{\sum_{i=1}^m \sum_{j=1}^n x_{ij}^2} ∣∣X∣∣F=i=1∑mj=1∑nxij2
torch.norm(torch.ones((4, 9)))
tensor(6.)
Equivalence then pulls this matrix into a vector , Then do the norm of the vector
QA
Q1: Why should machine learning be represented by tensors ?
Statistics use tensors to express .
Q2:copy and clone The difference between ?
copy Memory may not be copied , There are shallow copy and deep copy
clone Memory must be copied
Q3:torch Do not distinguish between line vectors and column vectors ?
If you want to distinguish line vectors and column vectors , You need to use a matrix .
If you use vectors , A vector is a one-dimensional array for a computer .
边栏推荐
- 20220605 Mathematics: divide two numbers
- What did I read in order to understand the to do list
- Training effects of different data sets (yolov5)
- Raspberry pie 4B deploys lnmp+tor and builds a website on dark web
- Hands on deep learning pytorch version exercise solution - 3.1 linear regression
- 【SQL】一篇带你掌握SQL数据库的查询与修改相关操作
- Inverse code of string (Jilin University postgraduate entrance examination question)
- High imitation Netease cloud music
- Ind wks first week
- Yolov5 creates and trains its own data set to realize mask wearing detection
猜你喜欢

Neural Network Fundamentals (1)
Anaconda安装包 报错packagesNotFoundError: The following packages are not available from current channels:

神经网络入门之矩阵计算(Pytorch)

Model evaluation and selection
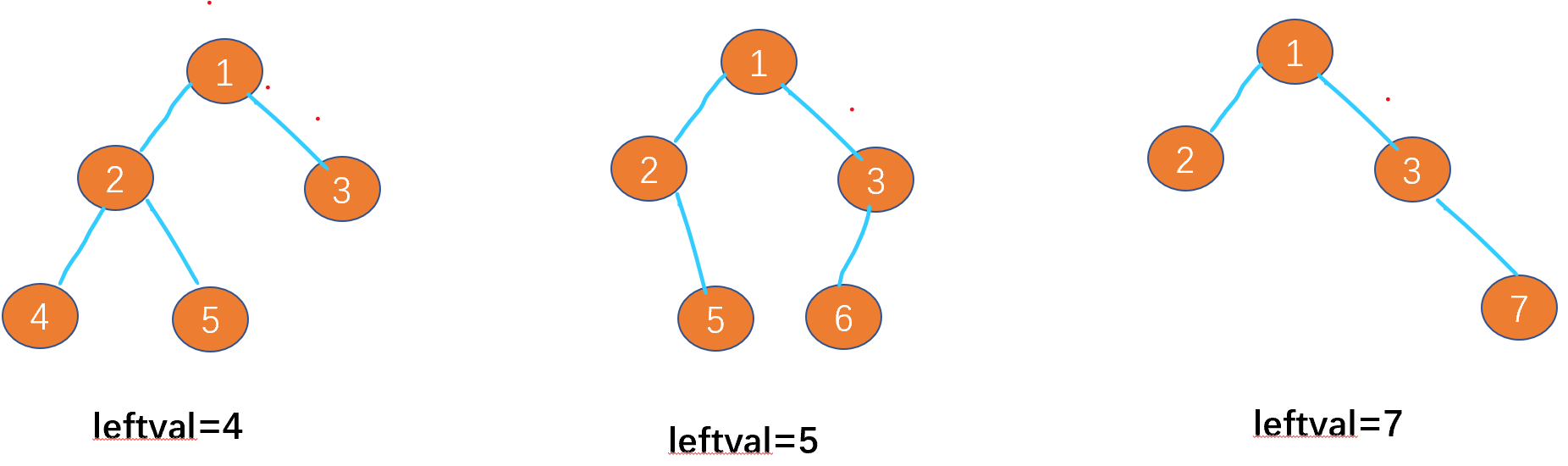
Leetcode-513:找树的左下角值
Yolov5 creates and trains its own data set to realize mask wearing detection

The imitation of jd.com e-commerce project is coming

Mise en œuvre d'OpenCV + dlib pour changer le visage de Mona Lisa

Timo background management system

Hands on deep learning pytorch version exercise answer - 2.2 preliminary knowledge / data preprocessing
随机推荐
20220608 other: evaluation of inverse Polish expression
QT creator uses OpenCV Pro add
20220607其他:两整数之和
Model evaluation and selection
Tensorflow—Image segmentation
Leetcode-404:左叶子之和
Ind FHL first week
一步教你溯源【钓鱼邮件】的IP地址
Leetcode刷题---1385
ECMAScript -- "ES6 syntax specification # Day1
Julia1.0
Leetcode刷题---189
Leetcode刷题---852
Are there any other high imitation projects
Tensorflow - tensorflow Foundation
Leetcode-106:根据中后序遍历序列构造二叉树
I really want to be a girl. The first step of programming is to wear women's clothes
Leetcode - 705 design hash set (Design)
What can I do to exit the current operation and confirm it twice?
Mise en œuvre d'OpenCV + dlib pour changer le visage de Mona Lisa