当前位置:网站首页>【九阳神功】2020复旦大学应用统计真题+解析
【九阳神功】2020复旦大学应用统计真题+解析
2022-07-06 09:20:00 【大师兄统计】
真题部分
一、(20分) 一家有两个孩子, 求下列事件的概率:
(1)(10分) 已知第一个是女孩, 求第二个是女孩的概率;
(2)(10分) 已知有一个是女孩, 求另一个是女孩的概率.
二、(15分) 甲有21个硬币, 乙有20个硬币, 两人同时抛出所有硬币, 求甲朝上的硬币数多于乙的概率.
三、(15分) 平面上有无数平行直线, 每两条平行直线间隔2米, 用边长1米的正三角形向平面投掷, 求三角形压到直线的概率.
四、(15分) 8个男生、7个女生坐成一排, 设 X i = 1 X_{i}=1 Xi=1表示第 i i i个位置与第 i + 1 i+1 i+1个位置坐的是异性, X i = 0 X_{i}=0 Xi=0表示第 i i i个位置与第 i + 1 i+1 i+1个位置坐的是同性, ξ = ∑ i = 1 14 X i , \xi=\sum_{i=1}^{14} X_{i}, ξ=∑i=114Xi, 求 E ξ . E \xi . Eξ.
五、(15分) 举出一个期望趋于正无穷, 却依概率收敛到0的随机变量序列 { X n } \left\{X_{n}\right\} { Xn}.
六、(20分) 有来自总体 X ∼ f ( x ) = θ x θ − 1 I { 0 < x < 1 } X \sim f(x)=\theta x^{\theta-1} I\{0<x<1\} X∼f(x)=θxθ−1I{ 0<x<1}的 n n n个随机样本, 求
(1)(5分) θ \theta θ 的 M L E , \mathrm{MLE}, MLE, 并验证无偏性;
(2)(5分) 验证MLE的一致性;
(3)(5分) θ \theta θ的矩估计;
(4)(5分) 利用样本中位数对 θ \theta θ进行估计.
七、(20分) X 1 , … , X n , X_{1}, \ldots, X_{n}, X1,…,Xn, i.i.d ∼ N ( μ , σ 2 ) , \sim N\left(\mu, \sigma^{2}\right), ∼N(μ,σ2), 证明 [ X ( 1 ) , X ( n ) ] \left[X_{(1)}, X_{(n)}\right] [X(1),X(n)]是 μ \mu μ的置信水平为 1 − 2 1 − n 1-2^{1-n} 1−21−n的置信区间.
八、(20分) 有来自总体 X ∼ f ( x ) = 1 2 e − ∣ x − θ ∣ X \sim f(x)=\frac{1}{2} e^{-|x-\theta|} X∼f(x)=21e−∣x−θ∣的7个随机样本, 求 θ \theta θ的MLE.
九、(10分) ( X 1 , X 2 ) ∼ N ( 0 , 0 ; 1 , 1 ; 0 ) , (X_1, X_2) \sim N(0,0 ; 1,1 ; 0), (X1,X2)∼N(0,0;1,1;0), 求 X 1 X 2 \frac{X_1}{X_2} X2X1的概率分布.
解析部分
一、(20分) 一家有两个孩子, 求下列事件的概率:
(1)(10分) 已知第一个是女孩, 求第二个是女孩的概率;
(2)(10分) 已知有一个是女孩, 求另一个是女孩的概率.
Solution:
(1) 首先需要假设:没有任何信息的情况下一个孩子是女孩的概率是 0.5 0.5 0.5.
用事件 A i A_{i} Ai 表示第 i i i 个是女孩 ( i = 1 , 2 ) (i=1,2) (i=1,2), 则 P ( A 2 ∣ A 1 ) = P ( A 1 A 2 ) P ( A 1 ) = 0.25 0.5 = 0.5 P\left(A_{2} \mid A_{1}\right)=\frac{P\left(A_{1} A_{2}\right)}{P\left(A_{1}\right)}=\frac{0.25}{0.5}=0.5 P(A2∣A1)=P(A1)P(A1A2)=0.50.25=0.5.
(2) P ( A 1 A 2 ∣ A 1 ∪ A 2 ) = P ( A 1 A 2 ) P ( A 1 ∪ A 2 ) = 0.25 0.75 = 1 3 P\left(A_{1} A_{2} \mid A_{1} \cup A_{2}\right)=\frac{P\left(A_{1} A_{2}\right)}{P\left(A_{1} \cup A_{2}\right)}=\frac{0.25}{0.75}=\frac{1}{3} P(A1A2∣A1∪A2)=P(A1∪A2)P(A1A2)=0.750.25=31.
二、(15分) 甲有21个硬币, 乙有20个硬币, 两人同时抛出所有硬币, 求甲朝上的硬币数多于乙的概率.
Solution:
根据对称性可以知道, P { P\{ P{ 甲朝上的硬币数多于乙 } = P { \}=P\{ }=P{ 甲朝下的硬币数多于乙 } \} }. 用 随机变量 X X X 表示甲朝上的硬币数, 随机变量 Y Y Y 表示乙朝上的硬币数.则:
P { X > Y } = P { 21 − X > 20 − Y } = P { 1 − X > − Y } = P { X < Y + 1 } = P { X ⩽ Y } \begin{aligned} P\{X>Y\} &=P\{21-X>20-Y\}=P\{1-X>-Y\} \\ &=P\{X<Y+1\}=P\{X \leqslant Y\} \end{aligned} P{ X>Y}=P{ 21−X>20−Y}=P{ 1−X>−Y}=P{ X<Y+1}=P{ X⩽Y}又 P { X > Y } + P { X ⩽ Y } = 1 P\{X>Y\}+P\{X \leqslant Y\}=1 P{ X>Y}+P{ X⩽Y}=1, 因此 P { X > Y } = P { X ⩽ Y } = 0.5 P\{X>Y\}=P\{X \leqslant Y\}=0.5 P{ X>Y}=P{ X⩽Y}=0.5.
三、(15分) 平面上有无数平行直线, 每两条平行直线间隔2米, 用边长1米的正三角形向平面投掷, 求三角形压到直线的概率.
Solution:
记 △ A B C \triangle A B C △ABC 的三条边分别为 a , b , c a, b, c a,b,c. 则三角形与平行线相交有以下几种情况:
(1) 三角形的一个顶点在平行线上;
(2)三角形的一条边与直线重合;
(3)三角形的两条 边与平行线相交.
根据概率的几何概型 P ( 1 ) = P ( 2 ) = 0 P(1)=P(2)=0 P(1)=P(2)=0, 因此仅需要考虑情况(3). 而 P ( 3 ) = P a b + P a c + P b c P(3)=P_{a b}+P_{a c}+P_{b c} P(3)=Pab+Pac+Pbc, 其中 P a b P_{a b} Pab 表示边 a 、 b a 、 b a、b 与平行线相交. 为此,记 P a P_{a} Pa 表示边 a a a 与平行线相交, 则 P a = P a c + P a b P_{a}=P_{a c}+P_{a b} Pa=Pac+Pab. 故 P ( 3 ) = 1 2 ( P a + P b + P c ) , P(3)=\frac{1}{2}\left(P_{a}+P_{b}+P_{c}\right), P(3)=21(Pa+Pb+Pc), 现仅需要求出 P a 、 P b 、 P c P_{a} 、 P_{b} 、 P_{c} Pa、Pb、Pc. 这是一个 Buffon 投针模型, 其概率是 P a = 2 a d π P_{a}=\frac{2 a}{d \pi} Pa=dπ2a, 其中 a a a 是边 a a a 的长度, d d d 是平行 线之间的间距,代入数据可算得 P a = 2 2 π = 1 π P_{a}=\frac{2}{2 \pi}=\frac{1}{\pi} Pa=2π2=π1. 同理 P b = P c = 1 π P_{b}=P_{c}=\frac{1}{\pi} Pb=Pc=π1. 故
P { 三角形压到直线 } = P ( 3 ) = 1 2 ( P a + P b + P c ) = 3 2 π . P\{\text { 三角形压到直线 }\}=P(3)=\frac{1}{2}\left(P_{a}+P_{b}+P_{c}\right)=\frac{3}{2 \pi}. P{ 三角形压到直线 }=P(3)=21(Pa+Pb+Pc)=2π3.
四、(15分) 8个男生、7个女生坐成一排, 设 X i = 1 X_{i}=1 Xi=1表示第 i i i个位置与第 i + 1 i+1 i+1个位置坐的是异性, X i = 0 X_{i}=0 Xi=0表示第 i i i个位置与第 i + 1 i+1 i+1个位置坐的是同性, ξ = ∑ i = 1 14 X i , \xi=\sum_{i=1}^{14} X_{i}, ξ=∑i=114Xi, 求 E ξ . E \xi . Eξ.
Solution:
E ξ = E ( ∑ i = 1 14 X i ) = ∑ i = 1 14 E X i E \xi=E\left(\sum_{i=1}^{14} X_{i}\right)=\sum_{i=1}^{14} E X_{i} Eξ=E(∑i=114Xi)=∑i=114EXi, 考虑到诸 X i X_{i} Xi 是同分布的, 现求 E X 1 E X_{1} EX1.
E X 1 = P ( X 1 = 1 ) = C 8 1 C 7 1 C 15 2 = 8 × 7 15 × 14 2 × 1 = 8 15 E X_{1}=P\left(X_{1}=1\right)=\frac{C_{8}^{1} C_{7}^{1}}{C_{15}^{2}}=\frac{8 \times 7}{\frac{15 \times 14}{2 \times 1}}=\frac{8}{15} EX1=P(X1=1)=C152C81C71=2×115×148×7=158 所以 E ξ = ∑ i = 1 14 E X i = 14 E X 1 = 112 15 E \xi=\sum_{i=1}^{14} E X_{i}=14 E X_{1}=\frac{112}{15} Eξ=∑i=114EXi=14EX1=15112.
五、(15分) 举出一个期望趋于正无穷, 却依概率收敛到0的随机变量序列 { X n } \left\{X_{n}\right\} { Xn}.
Solution:
给出这样一个随机变量序列: P ( X n = 0 ) = 1 − 1 n , P ( X n = n 2 ) = 1 n P\left(X_{n}=0\right)=1-\frac{1}{n}, P\left(X_{n}=n^{2}\right)=\frac{1}{n} P(Xn=0)=1−n1,P(Xn=n2)=n1. E X n = n → + ∞ E X_{n}=n \rightarrow+\infty EXn=n→+∞. 而 P ( X n ≠ 0 ) = 1 n P\left(X_{n} \neq 0\right)=\frac{1}{n} P(Xn=0)=n1, 则 X n → P 0 X_{n} \stackrel{P}{\rightarrow} 0 Xn→P0.
六、(20分) 有来自总体 X ∼ f ( x ) = θ x θ − 1 I { 0 < x < 1 } X \sim f(x)=\theta x^{\theta-1} I\{0<x<1\} X∼f(x)=θxθ−1I{ 0<x<1}的 n n n个随机样本, 求
(1)(5分) θ \theta θ 的 M L E , \mathrm{MLE}, MLE, 并验证无偏性;
(2)(5分) 验证MLE的一致性;
(3)(5分) θ \theta θ的矩估计;
(4)(5分) 利用样本中位数对 θ \theta θ进行估计.
Solution:
(1) 似然函数 L ( X ; θ ) = θ n ( ∏ i = 1 n x i ) θ − 1 L(\mathbf{X} ; \theta)=\theta^{n}\left(\prod_{i=1}^{n} x_{i}\right)^{\theta-1} L(X;θ)=θn(∏i=1nxi)θ−1, 对数似然函数 ln L = n ln θ + ( θ − 1 ) ∑ i = 1 n ln x i \ln L=n \ln \theta+(\theta-1) \sum_{i=1}^{n} \ln x_{i} lnL=nlnθ+(θ−1)∑i=1nlnxi. 令 ∂ ln L ∂ θ = n θ + ∑ i = 1 n ln x i = 0 \frac{\partial \ln L}{\partial \theta}=\frac{n}{\theta}+\sum_{i=1}^{n} \ln x_{i}=0 ∂θ∂lnL=θn+∑i=1nlnxi=0, 解得 θ ^ L = n ∑ i = 1 n ( − ln x i ) \hat{\theta}_{L}=\frac{n}{\sum_{i=1}^{n}\left(-\ln x_{i}\right)} θ^L=∑i=1n(−lnxi)n. 又因为总体服从贝塔分布, 属于 指数族分布, 其对数似然函数的驻点必定为极大似然估计. 所以 θ ^ L = n ∑ i = 1 n ( − ln x i ) \hat{\theta}_{L}=\frac{n}{\sum_{i=1}^{n}\left(-\ln x_{i}\right)} θ^L=∑i=1n(−lnxi)n 是 θ \theta θ 的极大似然估计. 若令 Y i = − ln X i ∼ Exp ( θ ) Y_{i}=-\ln X_{i} \sim \operatorname{Exp}(\theta) Yi=−lnXi∼Exp(θ), 且由伽马分布的可加性可知 T = ∑ i = 1 n y i ∼ G a ( n , θ ) T=\sum_{i=1}^{n} y_{i} \sim G a(n, \theta) T=∑i=1nyi∼Ga(n,θ), 则极 大似然估计可以写为 θ ^ L = n T \hat{\theta}_{L}=\frac{n}{T} θ^L=Tn.
E θ ^ L = E n T = ∫ 0 + ∞ n t θ n Γ ( n ) t n − 1 e − θ t d t = n θ Γ ( n ) ∫ 0 + ∞ ( θ t ) n − 2 e − θ t d ( θ t ) = n θ Γ ( n ) Γ ( n − 1 ) = n n − 1 θ E \hat{\theta}_{L}=E \frac{n}{T}=\int_{0}^{+\infty} \frac{n}{t} \frac{\theta^{n}}{\Gamma(n)} t^{n-1} e^{-\theta t} d t=\frac{n \theta}{\Gamma(n)} \int_{0}^{+\infty}(\theta t)^{n-2} e^{-\theta t} d(\theta t)=\frac{n \theta}{\Gamma(n)} \Gamma(n-1)=\frac{n}{n-1} \theta Eθ^L=ETn=∫0+∞tnΓ(n)θntn−1e−θtdt=Γ(n)nθ∫0+∞(θt)n−2e−θtd(θt)=Γ(n)nθΓ(n−1)=n−1nθ
所以 θ ^ L \hat{\theta}_{L} θ^L 不是 θ \theta θ 的无偏估计, 但它是渐进无偏的.
(2)上一小题中我们已经算得 E θ ^ L = n n − 1 θ → θ E \hat{\theta}_{L}=\frac{n}{n-1} \theta \rightarrow \theta Eθ^L=n−1nθ→θ, 现来考虑它的一致性.
E θ ^ L 2 = E n 2 T 2 = n 2 θ 2 Γ ( n ) ∫ 0 + ∞ ( θ t ) n − 3 e − θ t d ( θ t ) = n 2 θ 2 Γ ( n ) Γ ( n − 2 ) = n 2 ( n − 1 ) ( n − 2 ) θ 2 , E \hat{\theta}_{L}^{2}=E \frac{n^{2}}{T^{2}}=\frac{n^{2} \theta^{2}}{\Gamma(n)} \int_{0}^{+\infty}(\theta t)^{n-3} e^{-\theta t} d(\theta t)=\frac{n^{2} \theta^{2}}{\Gamma(n)} \Gamma(n-2)=\frac{n^{2}}{(n-1)(n-2)} \theta^{2}, Eθ^L2=ET2n2=Γ(n)n2θ2∫0+∞(θt)n−3e−θtd(θt)=Γ(n)n2θ2Γ(n−2)=(n−1)(n−2)n2θ2,
则 Var ( θ ^ L ) = E θ ^ L 2 − ( E θ ^ L ) 2 = n 2 θ 2 ( n − 1 ) ( n − 2 ) − n 2 θ 2 ( n − 1 ) 2 = n 2 ( n − 1 ) 2 ( n − 2 ) θ 2 \operatorname{Var}\left(\hat{\theta}_{L}\right)=E \hat{\theta}_{L}^{2}-\left(E \hat{\theta}_{L}\right)^{2}=\frac{n^{2} \theta^{2}}{(n-1)(n-2)}-\frac{n^{2} \theta^{2}}{(n-1)^{2}}=\frac{n^{2}}{(n-1)^{2}(n-2)} \theta^{2} Var(θ^L)=Eθ^L2−(Eθ^L)2=(n−1)(n−2)n2θ2−(n−1)2n2θ2=(n−1)2(n−2)n2θ2.
P ( ∣ θ ^ L − θ ∣ ≥ ε ) = P ( ∣ θ ^ L − n n − 1 θ + n n − 1 θ − θ ∣ ≥ ε ) P\left(\left|\hat{\theta}_{L}-\theta\right| \geq \varepsilon\right)=P\left(\left|\hat{\theta}_{L}-\frac{n}{n-1} \theta+\frac{n}{n-1} \theta-\theta\right| \geq \varepsilon\right) P(∣∣∣θ^L−θ∣∣∣≥ε)=P(∣∣∣∣θ^L−n−1nθ+n−1nθ−θ∣∣∣∣≥ε) ≤ P ( ∣ θ ^ L − n n − 1 θ ∣ ≥ ε 2 ) + P ( ∣ n n − 1 θ − θ ∣ ≥ ε 2 ) \leq P\left(\left|\hat{\theta}_{L}-\frac{n}{n-1} \theta\right| \geq \frac{\varepsilon}{2}\right)+P\left(\left|\frac{n}{n-1} \theta-\theta\right| \geq \frac{\varepsilon}{2}\right) ≤P(∣∣∣∣θ^L−n−1nθ∣∣∣∣≥2ε)+P(∣∣∣∣n−1nθ−θ∣∣∣∣≥2ε) 其中根据切比雪夫不等式 P ( ∣ θ ^ L − n n − 1 θ ∣ ≥ ε 2 ) ≤ 4 Var ( θ ^ L ) ε 2 = 4 ε 2 n 2 ( n − 1 ) 2 ( n − 2 ) θ 2 → 0 P\left(\left|\hat{\theta}_{L}-\frac{n}{n-1} \theta\right| \geq \frac{\varepsilon}{2}\right) \leq \frac{4 \operatorname{Var}\left(\hat{\theta}_{L}\right)}{\varepsilon^{2}}=\frac{4}{\varepsilon^{2}} \frac{n^{2}}{(n-1)^{2}(n-2)} \theta^{2} \rightarrow 0 P(∣∣∣θ^L−n−1nθ∣∣∣≥2ε)≤ε24Var(θ^L)=ε24(n−1)2(n−2)n2θ2→0 而对于较大的 n , P ( ∣ n n − 1 θ − θ ∣ ≥ ε 2 ) = 0 n, P\left(\left|\frac{n}{n-1} \theta-\theta\right| \geq \frac{\varepsilon}{2}\right)=0 n,P(∣∣n−1nθ−θ∣∣≥2ε)=0. 因此 P ( ∣ θ ^ L − θ ∣ ≥ ε ) → 0 P\left(\left|\hat{\theta}_{L}-\theta\right| \geq \varepsilon\right) \rightarrow 0 P(∣∣∣θ^L−θ∣∣∣≥ε)→0, 也就是说 θ ^ L \hat{\theta}_{L} θ^L 是 θ \theta θ 的一致估计.
(3) 总体服从 Beta ( θ , 1 ) \operatorname{Beta}(\theta, 1) Beta(θ,1), 由贝塔分布的数字特征, 我们知道 E X = θ θ + 1 E X=\frac{\theta}{\theta+1} EX=θ+1θ. 据此反解得出 θ \theta θ 的矩估计 θ ^ M = x ˉ 1 − x ˉ \hat{\theta}_{M}=\frac{\bar{x}}{1-\bar{x}} θ^M=1−xˉxˉ.
(4) 总体的分布函数是 F ( x ) = { 0 , x < 0 x θ , 0 ≤ x < 1 1 , x ≥ 1 F(x)=\left\{\begin{array}{cc}0, & x<0 \\ x^{\theta}, & 0 \leq x<1 \\ 1, & x \geq 1\end{array}\right. F(x)=⎩⎨⎧0,xθ,1,x<00≤x<1x≥1 令 F ( x ) = 1 2 F(x)=\frac{1}{2} F(x)=21, 解得 x 0.5 = ( 1 2 ) 1 θ x_{0.5}=\left(\frac{1}{2}\right)^{\frac{1}{\theta}} x0.5=(21)θ1, 用样本中位数 m 0.5 m_{0.5} m0.5 代替总体中位数 x 0.5 x_{0.5} x0.5, 并反解 出 θ ^ = 1 log 1 2 m 0.5 = log 1 2 1 2 log 1 2 m 0.5 = log m 0.5 1 2 \hat{\theta}=\frac{1}{\log _{\frac{1}{2}} m_{0.5}}=\frac{\log _{\frac{1}{2}} \frac{1}{2}}{\log _{\frac{1}{2}} m_{0.5}}=\log _{m_{0.5}} \frac{1}{2} θ^=log21m0.51=log21m0.5log2121=logm0.521 是基于样本中位数对 θ \theta θ 的估计.
七、(20分) X 1 , … , X n , X_{1}, \ldots, X_{n}, X1,…,Xn, i.i.d ∼ N ( μ , σ 2 ) , \sim N\left(\mu, \sigma^{2}\right), ∼N(μ,σ2), 证明 [ X ( 1 ) , X ( n ) ] \left[X_{(1)}, X_{(n)}\right] [X(1),X(n)]是 μ \mu μ的置信水平为 1 − 2 1 − n 1-2^{1-n} 1−21−n的置信区间.
Solution:
先考虑求 U = x ( 1 ) U=x_{(1)} U=x(1) 的分布, 由最小值分布的计算公式可知
F U ( u ) = 1 − [ 1 − Φ ( u − μ σ ) ] n F_{U}(u)=1-\left[1-\Phi\left(\frac{u-\mu}{\sigma}\right)\right]^{n} FU(u)=1−[1−Φ(σu−μ)]n 则 P ( μ < x ( 1 ) ) = 1 − F U ( μ ) = [ 1 − Φ ( 0 ) ] n = ( 1 2 ) n = 2 − n P\left(\mu<x_{(1)}\right)=1-F_{U}(\mu)=[1-\Phi(0)]^{n}=\left(\frac{1}{2}\right)^{n}=2^{-n} P(μ<x(1))=1−FU(μ)=[1−Φ(0)]n=(21)n=2−n.
根据对称性可知 P ( μ > x ( n ) ) = 2 − n P\left(\mu>x_{(n)}\right)=2^{-n} P(μ>x(n))=2−n. 所以 P ( x ( 1 ) ⩽ μ ⩽ x ( n ) ) = 1 − 2 ⋅ 2 − n = 1 − 2 1 − n P\left(x_{(1)} \leqslant \mu \leqslant x_{(n)}\right)=1-2 \cdot 2^{-n}=1-2^{1-n} P(x(1)⩽μ⩽x(n))=1−2⋅2−n=1−21−n
八、(20分) 有来自总体 X ∼ f ( x ) = 1 2 e − ∣ x − θ ∣ X \sim f(x)=\frac{1}{2} e^{-|x-\theta|} X∼f(x)=21e−∣x−θ∣的7个随机样本, 求 θ \theta θ的MLE.
Solution:
似然函数 L ( X ; θ ) = ( 1 2 ) 7 e − ∑ i = 1 7 ∣ x i − θ ∣ = ( 1 2 ) 7 e − ∑ i = 1 7 ∣ x ( i ) − θ ∣ L(\mathbf{X} ; \theta)=\left(\frac{1}{2}\right)^{7} e^{-\sum_{i=1}^{7}\left|x_{i}-\theta\right|}=\left(\frac{1}{2}\right)^{7} e^{-\sum_{i=1}^{7}\left|x_{(i)}-\theta\right|} L(X;θ)=(21)7e−∑i=17∣xi−θ∣=(21)7e−∑i=17∣x(i)−θ∣. 这里 x ( i ) x_{(i)} x(i) 表示的是第 i i i 次序统计量.为使似然函数尽量大, 则应使 e − ∑ i = 1 7 ∣ x ( 0 ) − θ ∣ e^{-\sum_{i=1}^{7}\left|x_{(0)}-\theta\right|} e−∑i=17∣x(0)−θ∣ 尽量大, 也就是使 ∑ i = 1 7 ∣ x ( i ) − θ ∣ \sum_{i=1}^{7}\left|x_{(i)}-\theta\right| ∑i=17∣∣x(i)−θ∣∣ 尽量小. 下面研究 ∑ i = 1 7 ∣ x ( i ) − θ ∣ \sum_{i=1}^{7}\left|x_{(i)}-\theta\right| ∑i=17∣∣x(i)−θ∣∣ 的性态:
∑ i = 1 7 ∣ x ( i ) − θ ∣ = ∑ i = 1 3 ( ∣ x ( i ) − θ ∣ + ∣ x ( 7 − i + 1 ) − θ ∣ ) + ∣ x ( 4 ) − θ ∣ \sum_{i=1}^{7}\left|x_{(i)}-\theta\right|=\sum_{i=1}^{3}\left(\left|x_{(i)}-\theta\right|+\left|x_{(7-i+1)}-\theta\right|\right)+\left|x_{(4)}-\theta\right| i=1∑7∣∣x(i)−θ∣∣=i=1∑3(∣∣x(i)−θ∣∣+∣∣x(7−i+1)−θ∣∣)+∣∣x(4)−θ∣∣ (上面这个式子将 x ( 1 ) , x ( 7 ) x_{(1)}, x_{(7)} x(1),x(7) 分为一组, x ( 2 ) , x ( 6 ) x_{(2)}, x_{(6)} x(2),x(6) 分为一组, x ( 3 ) , x ( 5 ) x_{(3)}, x_{(5)} x(3),x(5) 分为一组, x ( 4 ) x_{(4)} x(4) 单独一组)
其中 ∣ x ( i ) − θ ∣ + ∣ x ( 7 − i + 1 ) − θ ∣ \left|x_{(i)}-\theta\right|+\left|x_{(7-i+1)}-\theta\right| ∣∣x(i)−θ∣∣+∣∣x(7−i+1)−θ∣∣ 在 θ ∈ [ x ( i ) , x ( 7 − i + 1 ) ] \theta \in\left[x_{(i)}, x_{(7-i+1)}\right] θ∈[x(i),x(7−i+1)] 时取到最小值; ∣ x ( 4 ) − θ ∣ \left|x_{(4)}-\theta\right| ∣∣x(4)−θ∣∣ 在 θ = x ( 4 ) \theta=x_{(4)} θ=x(4) 时取到最小值. 而 ( ⋂ i = 1 3 [ x ( i ) , x ( 7 − i + 1 ) ] ) ∩ { x ( 4 ) } = { x ( 4 ) } \left(\bigcap_{i=1}^{3}\left[x_{(i)}, x_{(7-i+1)}\right]\right) \cap\left\{x_{(4)}\right\}=\left\{x_{(4)}\right\} (⋂i=13[x(i),x(7−i+1)])∩{ x(4)}={ x(4)}, 所以 θ ^ = x ( 4 ) \hat{\theta}=x_{(4)} θ^=x(4) 是 θ \theta θ 的 MLE.
九、(10分) ( X 1 , X 2 ) ∼ N ( 0 , 0 ; 1 , 1 ; 0 ) , (X_1, X_2) \sim N(0,0 ; 1,1 ; 0), (X1,X2)∼N(0,0;1,1;0), 求 X 1 X 2 \frac{X_1}{X_2} X2X1的概率分布.
Solution:
由于分母 X 2 X_{2} X2 的分布关于 0 对称, 因此 X 1 ∣ X 2 ∣ \frac{X_{1}}{\left|X_{2}\right|} ∣X2∣X1 与 X 1 X 2 \frac{X_{1}}{X_{2}} X2X1 同分布, 而很明显 N ( 0 , 1 ) χ 2 ( 1 ) 1 \frac{N(0,1)}{\sqrt{\frac{\chi^{2}(1)}{1}}} 1χ2(1)N(0,1) 是一个 自由度为 1 的 t t t 分布, 所以 X 1 ∣ X 2 ∣ \frac{X_{1}}{\left|X_{2}\right|} ∣X2∣X1 也是自由度为 1 的 t t t 分布, 它的概率密度是 f ( x ) = Γ ( 1 ) π Γ ( 1 2 ) ( x 2 + 1 ) − 1 = 1 π ⋅ 1 1 + x 2 , − ∞ < x < + ∞ , f(x)=\frac{\Gamma(1)}{\sqrt{\pi} \Gamma\left(\frac{1}{2}\right)}\left(x^{2}+1\right)^{-1}=\frac{1}{\pi} \cdot \frac{1}{1+x^{2}},-\infty<x<+\infty, f(x)=πΓ(21)Γ(1)(x2+1)−1=π1⋅1+x21,−∞<x<+∞, 即标准柯西分布.
边栏推荐
- FileInputStream和BufferedInputStream的比较
- [Topic terminator]
- MPLS experiment
- 最新坦克大战2022-全程开发笔记-2
- Tyut Taiyuan University of technology 2022 introduction to software engineering summary
- 分支语句和循环语句
- 初识指针笔记
- Share a website to improve your Aesthetics
- Relational algebra of tyut Taiyuan University of technology 2022 database
- Record: I accidentally wrote a recursion next time
猜你喜欢
4.二分查找

9.指针(上)
更改VS主题及设置背景图片

Summary of multiple choice questions in the 2022 database of tyut Taiyuan University of Technology
(超详细二)onenet数据可视化详解,如何用截取数据流绘图

The overseas sales of Xiaomi mobile phones are nearly 140million, which may explain why Xiaomi ov doesn't need Hongmeng
MYSQL索引钟B-TREE ,B+TREE ,HASH索引之间的区别和应用场景
4.分支语句和循环语句
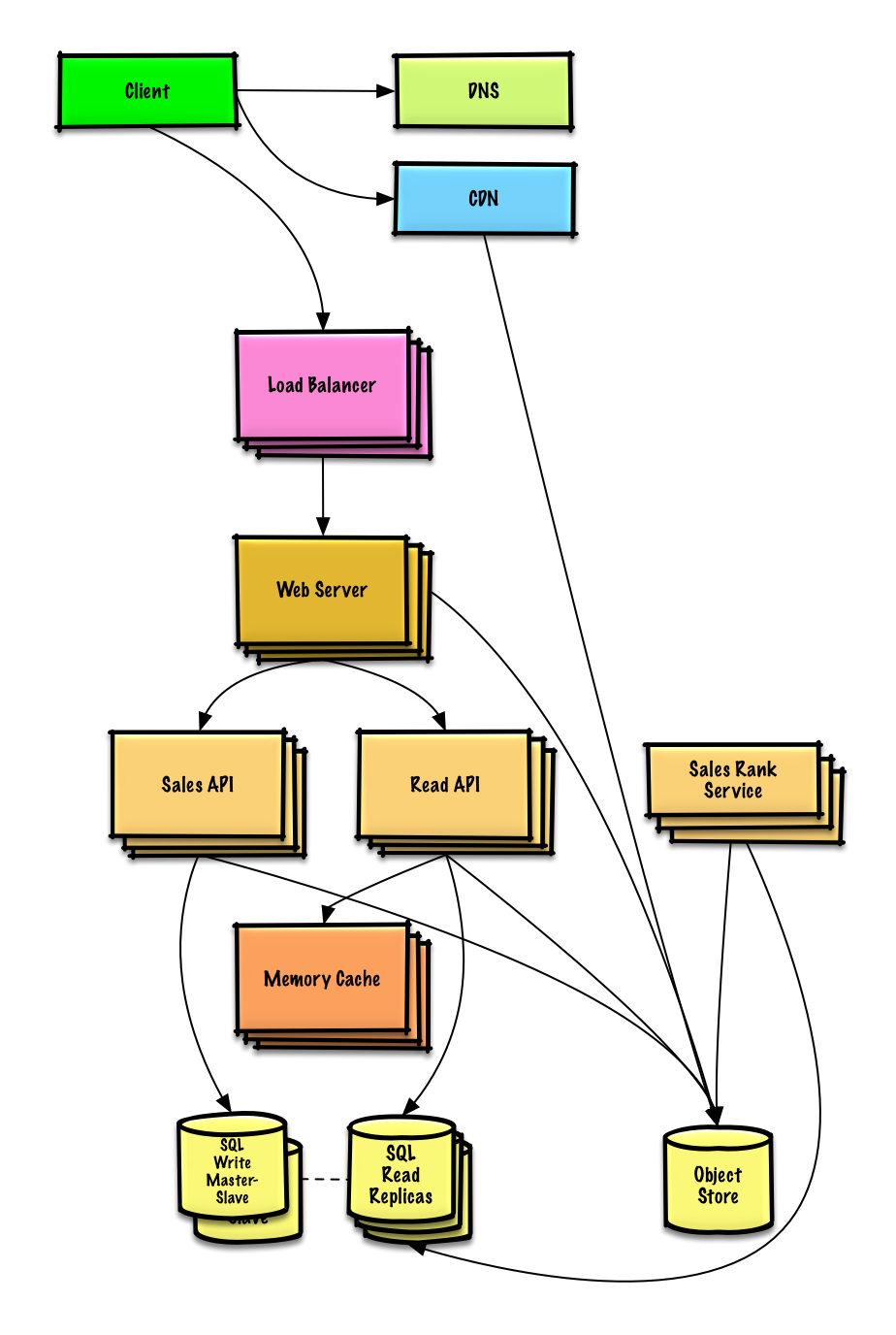
系统设计学习(三)Design Amazon‘s sales rank by category feature

TYUT太原理工大学2022数据库题库选择题总结
随机推荐
String类
TYUT太原理工大学2022软工导论简答题
Application architecture of large live broadcast platform
10 minutes pour maîtriser complètement la rupture du cache, la pénétration du cache, l'avalanche du cache
【话题终结者】
Questions and answers of "signal and system" in the first semester of the 22nd academic year of Xi'an University of Electronic Science and technology
System design learning (III) design Amazon's sales rank by category feature
Relational algebra of tyut Taiyuan University of technology 2022 database
面渣逆袭:Redis连环五十二问,三万字+八十图详解。
MYSQL索引钟B-TREE ,B+TREE ,HASH索引之间的区别和应用场景
How do architects draw system architecture blueprints?
13 power map
Set container
系统设计学习(一)Design Pastebin.com (or Bit.ly)
View UI plus released version 1.3.0, adding space and $imagepreview components
Questions and answers of "basic experiment" in the first semester of the 22nd academic year of Xi'an University of Electronic Science and technology
Summary of multiple choice questions in the 2022 database of tyut Taiyuan University of Technology
string
FileInputStream和BufferedInputStream的比较
TYUT太原理工大学2022软工导论考试题型大纲