二叉树专题--AcWing 1497. 树的遍历（利用后、中序遍历，构建二叉树）

本题十分重要，不论在算法竞赛，或是笔试面试中，都经常出现。

题意：

告诉我们一棵二叉树的 中序遍历 和 后序遍历，要我们输出其 层序遍历（即 BFS 序）

思路：

先利用二叉树的 中序遍历和后序遍历，将二叉树建立，之后 利用 BFS 输出其层序遍历的顺序。

我们模拟一下样例的建树过程：

根据题中的 Sample Input，我们得知给定二叉树的中、后序遍历：

• 中序：1 2 3 4 5 6 7
• 后序：2 3 1 5 7 6 4

首先，对于后序遍历来说，根节点肯定是最后一个点，因此 “4” 一定是根节点。之后，我们在中序遍历中找到 “4” 号点，在中序遍历中，我们一定是在 “4” 号点左边遍历左子树（三个点：1 2 3），在其右边遍历右子树（三个点：5 6 7）。

由于 后序遍历是先遍历左子树，后遍历右子树，最后遍历根。根据之前得出的 4 号点左、右子树大小为 3，因此我们发现，左子树的后序遍历应当为：2 3 1（大小也为 3），右子树的后序遍历为：5 7 6。

• 我们试着往左递归一层（4 号节点左子树），由于之前得到了左子树后序遍历（2 3 1），根据 “后序遍历根节点为最后一个点” 的原则可知 左子树的根节点为 1，之后再中序遍历中找到 1 号点的位置，发现 1 号点左侧不存在节点，说明 1 号点左子树为 空，右侧存在 2 个点 2 3，即：1 号节点右子树包含节点 2 3。在后序遍历中，由于 2 3 是后序遍历的结果，因此 3 就是 1 号节点右子树的根节点，在中序遍历中 2 在 3 的左侧，至此，我们将 1 号节点的左子树 也建立好了。

• 往右递归一层（4 号节点右子树），类似与上面的分析过程不难得到。

对于样例，我们最终得到的二叉树如下：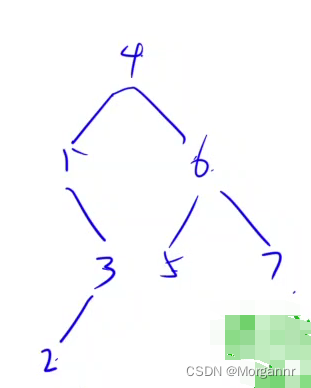

小结一下，本题要抓住两点核心：

• 后序遍历中，最后一个点一定是根节点
• 在中序遍历中，先找到根节点的位置，左子树在跟的左侧，右子树在根的右侧

其中，在中序遍历中可以利用哈希表 O(1) 的复杂度 找到根节点的位置。

我们以代码实现为目的，进一步将该过程进行抽象：

• 每次找到中序遍历中根所在的位置，该位置左侧为左子树中序遍历，右侧为右子树中序遍历，接下来可以看看左子树区间长度（包含多少节点）。

• 在后序遍历中，我们一定是先遍历左子树，后遍历右子树，最后遍历根节点，至此，左、右子树中、后序遍历都已找到，接下来递归左子树（即给定左子树中序遍历和后序遍历，递归构建左子树），右子树同理递归进行。

• 通过递归的方式将整棵树重建：当前节点是根，根的左侧递归构建左子树，返回左子树根节点，并将左子树根节点插到根的左儿子位置，同理处理右子树。

如果我们将树上的每个节点都看做是一个单独的根节点，那么整个的递归过程相当于是每次都查找根节点并插入，逐步建树，这样更好理解。

这样我们就将整棵树构建出来了。建出整棵树后，从根节点开始 BFS 即可。

以上整个过程复杂度是 O(n) ，每个节点处理一次。输入保证所有点的权值都不一样，如果所有权值都一样就不能在 O(n) 的时间复杂度完成了（对应的二叉树可能不唯一）

代码：

（不带注释，在下方代码基础上有所改动）

#define _CRT_SECURE_NO_WARNINGS 1
#include <bits/stdc++.h>

using namespace std;
#define int long long
#define map unordered_map
const int N = 40;
int in[N], post[N];
map<int, int> l, r, d;

int build(int il, int ir, int pl, int pr)
{
    if(pl > pr) return 0;
    int root = post[pr];
    int k = d[root];
    l[root] = build(il, k - 1, pl, k - 1 - il + pl);
    r[root] = build(k + 1, ir, k - il + pl, pr - 1);
    return root;
}

void bfs(int root)
{
    queue<int> q; q.push(root);
    cout << root << ' ';

    while (!q.empty())
    {
        int t = q.front(); q.pop();

        if(l[t]) cout << l[t] << ' ', q.push(l[t]);

        if(r[t]) cout << r[t] << ' ', q.push(r[t]);
    }
    puts("");
}

signed main()
{
    int T = 1; //cin >> T;

    while (T--)
    {
        int n; cin >> n;
        for (int i = 0; i < n; ++i) cin >> post[i];
        for (int i = 0; i < n; ++i) cin >> in[i], d[in[i]] = i;
        int root = build(0, n - 1, 0, n - 1);
        bfs(root);
    }

    return 0;
}

（加注释）

#define _CRT_SECURE_NO_WARNINGS 1
#include <bits/stdc++.h>

using namespace std;
#define int long long
#define map unordered_map
const int N = 40;
int in[N], post[N];	//中序遍历 后序遍历
map<int, int> l, r, d;	//分别表示：各个点的 左儿子 右儿子 ，中序遍历中每个节点对应的下标

int build(int il, int ir, int pl, int pr)	//当前子树 中序遍历的左右端点 后序遍历的左右端点
{
    
	int root = post[pr];	//后序遍历最后一个点 即根节点
	int k = d[root];	//查表，在中序遍历中找到根节点下标

	//如果我们将树上的每个节点都看做是一个单独的根节点，那么整个的递归过程相当于是每次都查找根节点并逐步建树，这样更好理解
	
	//下方递归传入的参数 根据后、中序遍历的原则，并利用两种遍历区间长度相等的原则解方程 来确定，在纸上画图很好想
	
	if (il < k) l[root] = build(il, k - 1, pl, k - 1 - il + pl);
	if (ir > k) r[root] = build(k + 1, ir, k - il + pl, pr - 1);
	return root;	//返回值是根节点
}

void bfs(int root)
{
    
	queue<int> q; q.push(root);
	cout << root << ' ';

	while (!q.empty())
	{
    
		int t = q.front(); q.pop();
		
		if (l.count(t)) {
    
			cout << l[t] << ' ';
			q.push(l[t]);
		}

		if (r.count(t)) {
    
			cout << r[t] << ' ';
			q.push(r[t]);
		}
	}
	puts("");
}

signed main()
{
    
	int T = 1; //cin >> T;

	while (T--)
	{
    
		int n; cin >> n;
		for (int i = 0; i < n; ++i) cin >> post[i];	//后序
		for (int i = 0; i < n; ++i) cin >> in[i], d[in[i]] = i;	//中序 同时要在哈希表中存每个点下标
		int root = build(0, n - 1, 0, n - 1);	//递归构建整棵二叉树
		bfs(root);
	}

	return 0;
}