Eight basic sorting (detailed explanation)

Preface
Bloggers will talk about choice , Insert , hill , Fast , Bubbling , Stack row , Merge sort , Count sort .

1. Insertion sort

1.1 Direct insert sort

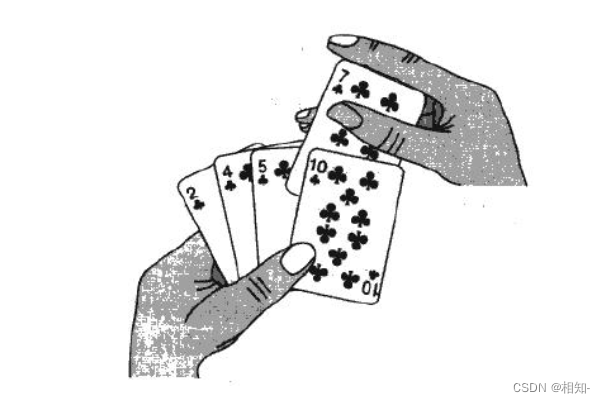
Dynamic diagram demonstration :

Ideas :

Like when we play cards , One by one

The specific idea is , We insert a number into an ordered array , So we compare the numbers in an ordered array , So how do we insert this data ? We use the coverage method , It is to cover the last number with the previous number in this order , This will leave a space for the data we want to insert , Then insert it , Maybe you have questions , How do we insert an unordered array ??? In fact, we regard the first number as an array , Then he is orderly , Then insert the second number , Insert the third number . . . . . . ., This completes the sorting

Code implementation

void InsertSort(int* a, int n)
{
    
	for (int i = 0; i < n-1; i++)// Can be divided into n-1 Insert... Times , The first time I thought it was orderly ,
	{
    
		int end = i;// Record the last position of the ordered array inserted each time 
		int tmp = a[end + 1];// Record the inserted data 
		while (end >= 0)// All the way to 0 Subscript location 
		{
    
			if (tmp< a[end])
			{
    
				a[end + 1] = a[end];// Cover back 
				--end;
			}
			else
			{
    
				break;
			}
			a[end + 1] = tmp;// Insert , You can't put it in else in , Because it could be else in break come out   It could be end>=0 For the sake of falsehood , in other words tmp Is the smallest number in an ordered array 
		}	
		//  It's OK to put it here  a[end + 1] = tmp;// Insert , You can't put it in else in , Because it could be else in break come out   It could be end>=0 For the sake of falsehood , in other words tmp Is the smallest number in an ordered array 
	}
}

Complexity

Spatial complexity :

O(1), No additional space has been opened up

Time complexity :

The best situation : In order , Just go through it once , namely O(N)
The worst case scenario : Every time you insert a number, you must traverse , namely F(N)=1+2+3+4+…+N=N(N-1)/2=O(N^2).

1.2 Shell Sort ( Reduced delta sort )

Hill's ranking method is also called reducing increment method . The basic idea of Hill's ranking is ： Choose an integer first , Divide all the records in the file to be sorted into groups , All records at a distance of are in the same group , And sort the records in each group . then , Take and repeat the above grouping and sorting . When they arrive in =1 when , All records are arranged in a unified group .

Dynamic diagram demonstration :

Draw pictures to explain :

It can be seen from the picture that gap The bigger it is , The more small arrays you divide into , Hill sorting is through this inter cell pre scheduling , Let the array appear ordered , This reduces the last direct insert sort (gap=1) The number of iterations , To speed up !

Code

void ShellSort(int* a, int n)
{
    
	int gap = n;
	while (gap > 1)
	{
    
		gap = gap / 3 + 1;// avoid gap=0, Cause the last time not to 1, So add 1, When it comes to 1 It's time to insert sort 
		for (int i = 0; i < n - gap; i++)
		{
    
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)// Split multiple groups of arrays for insert sort 
			{
    
				if (tmp < a[end])
				{
    
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
    
					break;
				}
				a[end + gap] = tmp;
			}
		}
	}
}

A summary of the characteristics of Hill sort ：

1. Hill sort is an optimization of direct insert sort .
2. When gap > 1 It's all pre sorted , The goal is to make arrays more ordered . When gap == 1 when , The array is nearly ordered , This will soon . So on the whole , Can achieve the effect of optimization . We can compare the performance test after implementation .
3. The time complexity of Hill sort is not easy to calculate , because gap There are many ways to get the value of , Makes it difficult to calculate . But a large number of experiments have proved that O(N^1.3) about

2. Selection sort

2.1.1 One way selection sorting

Ideas

Is to find the maximum value in the array , Then put it on the far left , Discharge in sequence

Dynamic diagram demonstration :

Code :

void SelectSort(int* a, int n)
{
    

	for (int i = 0; i < n; i++)
	{
    
		int index = i;
		for (int j = i + 1; j < n; j++)// Find the most valuable subscript 
		{
    
			if (a[index] < a[j])
			{
    
				index = j;
			}
		}
		Swap(&a[index], &a[i]);
	}
}

2.1.2 Bidirectional selection sorting ( Optimization of one-way selective sorting )

Code

void SelectSort2(int* a, int n)
{
    
	int begin = 0;
	int end = n-1;
	while(begin<end)
	{
    

		int maxi = begin;
		int mini = begin;
		for (int j = begin; j <= end; j++)
		{
    
			if (a[maxi] < a[j])
			{
    
				maxi = j;
			}
			if (a[mini] > a[j])
			{
    
				mini = j;
			}
		}
		Swap(&a[maxi], &a[begin]);
		if (mini == begin)// Because of the above exchange ,maxi and begin Exchanged , When mini==begin when , explain begin Is the minimum , But and maxi Exchanged , therefore maxi Now it's the minimum 
		{
    
			mini = maxi;	
		}
		int temp = 0;
		Swap(&a[mini], &a[end]);

		begin++;
		end--;
	}
}

Complexity

Time complexity :O(N^2)
Spatial complexity :O(1)

2.2 Heap sort

Look at my article : Implementation of binary heap ( Including heap sorting explanation ), Click through

3. Exchange sort

3.1 Bubble sort

Ideas :

Adjacent data are compared and exchanged in turn

Code :

void BubbleSort(int* a, int n)
{
    

	for (int j = 0; j < n - 1; ++j)
	{
    
		int exchange = 0;
		for (int i = 1; i < n - j; ++i)
		{
    
			if (a[i - 1] > a[i])
			{
    
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}

		if (exchange == 0)//exchange==0 It indicates that the data is in order 
		{
    
			break;
		}
	}
}

3.2 Quick sort

thought ;

Take any element in the element sequence to be sorted as the reference value , According to the sorting code, the set to be sorted is divided into two subsequences , All elements in the left subsequence are less than the base value , All elements in the right subsequence are greater than the base value , Then the leftmost and rightmost subsequences repeat the process , Until all the elements are aligned in their respective positions .
Key solutions , Single trip key The location of

The code template :

void QuickSort(int* a, int begin, int end)
{
    

	while (begin >= end)
		return;
	int keyi = PartSort(a, begin, end);
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);

}

It is very similar to the preorder traversal of a binary tree ! Is to divide the array into the smallest cells , Then the smallest cell is ordered , Then go up to the next floor key Values are ordered on both sides , And so on , To complete the order !!

3.2.1 hoare edition

Ideas

First from key Find small in the opposite direction of , hypothesis key On the left , Let's let the one on the right right Find the ratio key A small pause , Then let the one on the left left Looking for big , After finding and right In exchange for , then right Keep looking ,left Then I also look for , Find and exchange , Know that after meeting , The left side of the meeting position is Dubi key Small , On the right, there's more than key Big , We let key The value of is exchanged with the meeting point , then key To the point of contact , This completes the single exchange , And then to key Left side , On the right are an array , Then complete the exchange !!

Moving graph

Code :

int PartSort(int* a, int begin, int end)//hoare edition   It's like walking first and then looking key Location 
{
    
	int left = begin;
	int keyi = left;
	int right = end;
	while (left < right)
	{
    

		while (left < right && a[right] >= a[keyi])// Looking for a small 
			// Why do we start here keyi In the opposite direction ??  Because in left and right When we met , The ratio of the values encountered a[keyi] Small or equal , Even if right All the way to keyi Location doesn't matter 
			// That's why right Is to find a small one , The most extreme is equality , Because the small ones go first , So it must be small when we meet , If from keyi If you go in the right direction , It must be a big meeting , Big and a[keyi] Exchange is definitely wrong 
			// We just need to find a small exchange ,  What's the matter with you looking for a big one ?
		{
    
			right--;
		}
		while (left < right && a[left] <= a[keyi])// Looking for big 
		{
    
			left++;
		}
		Swap(&a[right], &a[left]);
	}
	Swap(&a[keyi], &a[left]);
	keyi = left;
	return keyi;
}

3.2.2 Excavation method

Ideas

take key As a pit , then right The pointer starts to look small , Find the small one and put it in the pit ( It's exchange ), then left Looking for big , Find it and put it in the pit , Until two pointers meet and stop , Then the place where we met must be a pit , take key The raw data is put into the pit ,key The location of the pit becomes the location of the pit , and hoare The version is very similar to , But it's easier to understand ! This completes the single pass sorting !

Moving graph

Code

int PartSort(int* a, int begin, int end)// Excavation method , Effectively help you understand   It's like walking and looking key Location 
{
    
	int key = a[begin];
	int piti = begin;// Pit position 
	while (begin < end)
	{
    
		// Find the big one from the left , Find it and put it in the pit , Then it becomes a new pit 
		while (begin < end && a[end] >= key)
		{
    
			end--;
		}
		a[piti] = a[end];// Put the large value into the pit 
		piti = end;// Pit position to the original large value position 
		// Find the small one from the left , Find it and put it in the pit , Then it becomes a new pit 
		while (begin < end && a[begin] <= key)
		{
    
			begin++;
		}
		a[piti] = a[begin];// Put the small value into the pit 
		piti = begin;// Pit position to the original small value position 
	}
	a[piti] = key;
	return piti;// The last pit is ours key value 
}

3.2.3 Front and back pointer method

Ideas

Front pointer cur, The back pointer prev, The front pointer looks for the ratio in the front key Low value , Find it and prev Swap places , then prev+1, repeat , Last prev The position of is key The dividing point of , So let that key and prev In exchange for

Moving graph

Code

int PartSort3(int* a, int begin, int end)// Front and back pointer method   The code is the most concise 
{
    
	int cur = begin+1;
	int prev = begin;
	int keyi = begin;
	for (int i = begin; i < end; i++)
	{
    
		if (a[cur] <= a[keyi]&& prev++!=cur)// Looking for big , Find the last prev Move back a position and cur Swap places , Namely cur Go find big value , Find it and go prev Over there , Finish prev Just run one 
		{
    
			Swap(&a[prev], &a[cur]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);// take keyi The corresponding values and prev In exchange for , Give Way keyi Become a dividing line !
	keyi = prev;
	return keyi;
}

Quicksort optimization

Optimize 1:

If we had studied binary trees , We should be key In the middle of the array , The smaller the depth of this traversal , And if every time you choose key Is the maximum or minimum value of this group of numbers , The efficiency of fast platoon will become very low , Almost close to O(N²), It may also lead to stack overflow due to too deep recursion ., So we take the middle of three numbers to optimize !

Code

int GetMidIndex(int* a, int begin, int end)// The triple value is taken as the middle 
{
    
	int mid = (begin + end) / 2;
	if (a[begin] < a[mid])
	{
    
		if (a[mid] < a[end])
			return mid;
		else if (a[begin] < a[end])
			return end;
		else
			return begin;
	}
	else //(a[begin] >= a[mid])
	{
    
		if (a[mid] > a[end])
			return mid;
		else if (a[begin] < a[end])
			return begin;
		else
			return end;
	}
}

Optimize 2

Need to know , The fast algorithm is to recursively arrange the left and right sides of a number , So when the fast scheduling algorithm gets closer and closer to the end , The closer the left and right arrays are to order .
The fast sorting algorithm has no efficiency improvement for the near ordered sequences , But we know that when inserting sorting , If a sequence is closer to order , The more efficient the insertion sort is .
So we can use insert sort to optimize !!

Code

void QuickSort(int* a, int begin, int end)
{
    

	while (begin >= end)
		return;
	while (end - begin > 20)// Optimize , Because the smaller the recursion number, the more , It's not worth it 
	{
    
		int keyi = PartSort3(a, begin, end);
		QuickSort(a, begin, keyi - 1);
		QuickSort(a, keyi + 1, end);
	}
	InsertSort(a, end - begin+1);// Array subscript difference +1 Equal to the number of arrays 

}

Quick sort non recursive version

Ideas :

When designing a single sequence , We need to know how to change the header and footer of the array , So we use the stack to realize non recursion , Push the head and tail into the stack in turn , And then it will be out of the stack before a single sort , Get one keyi value , So we know the head and tail of the left and right subintervals , Continue stack pressing , This is similar to the sequence traversal of binary tree

Code

void QuickSortNonR(int* a, int begin, int end)// Fast sorting non recursive methods 
{
    
	Stack q;
	StackInit(&q);
	StackPush(&q, end);
	StackPush(&q, begin);
	while (!StackEmpty(&q))
	{
    
		int left = StackTop(&q);
		StackPop(&q);
		int right = StackTop(&q);
		StackPop(&q);
		int keyi = PartSort3(a, left, right);
		// Section [keyi-1,left] keyi [keyi+1,right]
		if (keyi + 1 < right)
		{
    
			StackPush(&q, right);// Because first top Yes. left, therefore left Side last put 
			StackPush(&q, keyi+1);
		}
		if (keyi - 1 > left)
		{
    
			StackPush(&q, keyi-1);// Because first top Yes. left, therefore left Side last put 
			StackPush(&q, left);
		}
	}
	StackDestroy(&q);
}